5 20 As A Percent
saludintensiva
Sep 13, 2025 · 4 min read
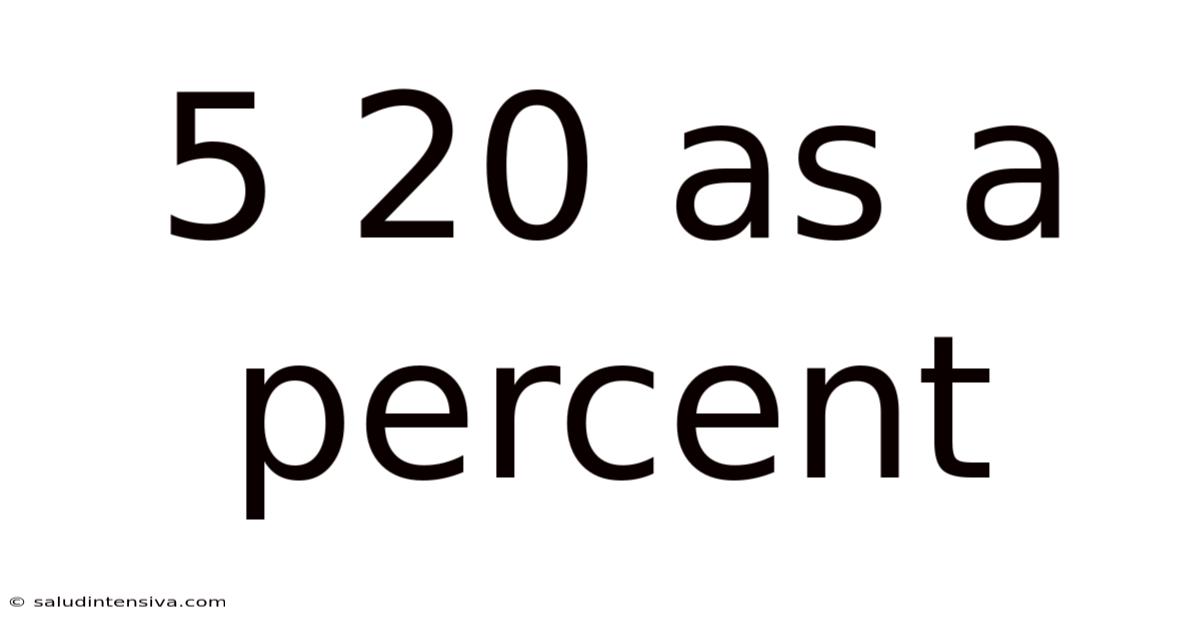
Table of Contents
Decoding 5/20 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is fundamental to many aspects of life, from calculating discounts in a store to comprehending financial reports. This article will thoroughly explore how to convert the fraction 5/20 into a percentage, explaining the process step-by-step and providing a deeper understanding of the underlying mathematical concepts. We'll also delve into practical applications and address frequently asked questions. By the end, you'll not only know the answer but also possess a solid grasp of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion, let's clarify the basics. A fraction represents a part of a whole. In the fraction 5/20, '5' is the numerator (the part) and '20' is the denominator (the whole). A percentage, on the other hand, expresses a fraction as parts per hundred. The symbol '%' signifies "per cent" or "out of 100".
Converting 5/20 to a Percentage: A Step-by-Step Guide
There are two primary methods to convert 5/20 to a percentage:
Method 1: Simplifying the Fraction and then Converting
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This simplifies the calculation and makes it easier to understand.
-
Simplify the Fraction: Find the greatest common divisor (GCD) of the numerator (5) and the denominator (20). The GCD of 5 and 20 is 5. Divide both the numerator and the denominator by the GCD:
5 ÷ 5 = 1 20 ÷ 5 = 4
This simplifies the fraction 5/20 to 1/4.
-
Convert the Simplified Fraction to a Decimal: Divide the numerator (1) by the denominator (4):
1 ÷ 4 = 0.25
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage sign (%):
0.25 × 100 = 25%
Therefore, 5/20 is equal to 25%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying it first.
-
Convert the Fraction to a Decimal: Divide the numerator (5) by the denominator (20):
5 ÷ 20 = 0.25
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage sign (%):
0.25 × 100 = 25%
This method also yields the same result: 25%. Both methods are equally valid; choose the one you find more convenient.
Illustrative Examples: Real-World Applications
Let's see how this conversion applies in different scenarios:
-
Test Scores: Imagine a student scored 5 out of 20 on a quiz. Converting 5/20 to a percentage (25%) gives a clear picture of their performance. They answered 25% of the questions correctly.
-
Sales and Discounts: A store offers a discount of 5 out of every 20 items. This represents a 25% discount.
-
Surveys and Polls: If 5 out of 20 respondents answered "yes" to a survey question, 25% of respondents gave a "yes" answer.
-
Financial Calculations: Understanding percentages is critical in finance, whether it's calculating interest rates, analyzing investment returns, or understanding profit margins. Converting fractions to percentages simplifies the analysis of financial data.
A Deeper Dive into Percentage Calculations: Understanding Ratios and Proportions
The conversion from fraction to percentage is fundamentally a manipulation of ratios and proportions. A ratio is a comparison of two quantities, often expressed as a fraction. A proportion is a statement of equality between two ratios.
In the case of 5/20, the ratio is 5:20. To express this ratio as a percentage (a ratio out of 100), we set up a proportion:
5/20 = x/100
Solving for 'x' (the percentage):
x = (5/20) * 100 = 25
This confirms that 5/20 represents 25%.
This understanding of ratios and proportions enhances the comprehension of percentage calculations and allows for solving more complex problems.
Frequently Asked Questions (FAQs)
Q1: Can any fraction be converted into a percentage?
A1: Yes, absolutely. Any fraction can be converted to a percentage by dividing the numerator by the denominator and then multiplying the result by 100.
Q2: What if the resulting decimal has many digits after the decimal point?
A2: You can round the decimal to the desired level of accuracy (e.g., to two decimal places). In many practical situations, rounding is acceptable.
Q3: What if the denominator is zero?
A3: Division by zero is undefined in mathematics. A fraction with a denominator of zero is not a valid mathematical expression.
Q4: Are there online calculators to convert fractions to percentages?
A4: Yes, many online calculators are readily available to perform this conversion quickly and efficiently. However, understanding the underlying process is crucial for comprehending the concept and applying it effectively in various situations.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental skill with far-reaching applications. By understanding the process, whether through simplifying the fraction or direct decimal conversion, you gain a valuable tool for interpreting data and solving problems in numerous fields. The method presented here, along with the illustrative examples and FAQs, provides a solid foundation for mastering percentage calculations. Remember that the core concept lies in understanding ratios and proportions – the foundation upon which all percentage conversions are built. Practice these methods, and you'll confidently navigate the world of percentages.
Latest Posts
Latest Posts
-
4 To The Power 0
Sep 13, 2025
-
Gcf Of 42 And 24
Sep 13, 2025
-
Least To Greatest Calculator Decimals
Sep 13, 2025
-
19 50 As A Decimal
Sep 13, 2025
-
2 7 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.