5 23 As A Percent
saludintensiva
Sep 22, 2025 · 5 min read
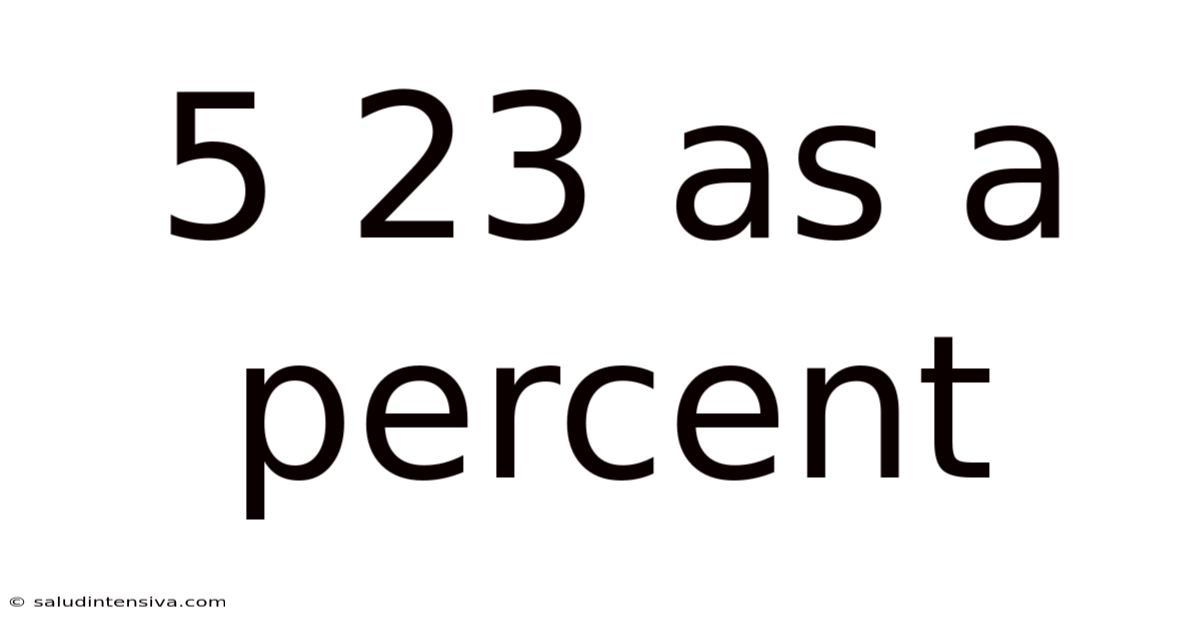
Table of Contents
5/23 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This article will delve deep into converting the fraction 5/23 into a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and addressing common questions. We'll also examine practical applications and explore similar fraction-to-percentage conversions to solidify your understanding.
Introduction: Understanding Fractions and Percentages
Before diving into the specifics of 5/23, let's briefly recap the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of one hundred. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2. Converting fractions to percentages allows us to express fractional values in a standardized and readily understandable format.
Converting 5/23 to a Percentage: A Step-by-Step Approach
The conversion process involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
5 ÷ 23 ≈ 0.21739
We use the approximation symbol (≈) because the division results in a non-terminating decimal (a decimal that goes on forever without repeating). We'll need to round the decimal to a suitable number of decimal places for practical purposes. For now, we'll keep a few extra decimal places for accuracy.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.21739 × 100 ≈ 21.739%
Therefore, 5/23 is approximately equal to 21.74% when rounded to two decimal places. This is a common level of precision for most practical applications.
Understanding the Approximation
It's crucial to understand that our result is an approximation. The decimal representation of 5/23 is an irrational number – it cannot be expressed as a simple fraction or a terminating decimal. Rounding introduces a small degree of error. The more decimal places we retain, the more accurate our percentage will be, but for most purposes, two decimal places are sufficient.
Alternative Methods for Conversion
While the division method is the most straightforward, let's explore an alternative approach that might offer a clearer understanding of the underlying principles:
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Ideally, we'd want to find a fraction equivalent to 5/23 that has a denominator of 100. This would directly give us the percentage. However, there's no integer value that, when multiplied by 23, equals 100. This highlights why the decimal conversion method is generally preferred for fractions like 5/23.
The Mathematical Principles Behind the Conversion
The conversion process hinges on the fundamental relationship between fractions, decimals, and percentages. They all represent proportions or parts of a whole. The key to conversion lies in understanding that:
- A percentage is a fraction with a denominator of 100.
- A decimal is a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.).
- We can convert between fractions and decimals through division and multiplication.
Practical Applications of Fraction-to-Percentage Conversions
Converting fractions to percentages is frequently used in various real-world scenarios:
- Calculating grades: If you answered 5 out of 23 questions correctly on a test, your score is approximately 21.74%.
- Analyzing data: In statistics, representing data as percentages provides a clear and concise way to compare proportions.
- Financial calculations: Percentages are essential in calculating interest rates, discounts, taxes, and other financial computations.
- Everyday life: Understanding percentages helps in comparing prices, understanding sales, and making informed decisions related to budgeting and shopping.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 5/23 to a percentage?
A1: Absolutely! Most calculators have a division function. Simply divide 5 by 23, then multiply the result by 100 to get the percentage.
Q2: What if I need a more precise percentage than 21.74%?
A2: You can use a calculator or computer software to perform the division to a greater number of decimal places. The more decimal places you retain, the more accurate your percentage will be.
Q3: Are there any online tools that can help with fraction-to-percentage conversions?
A3: Yes, numerous online calculators and converters are available. These tools can quickly and efficiently perform the conversion for you.
Q4: Why is the result an approximation and not an exact value?
A4: Because the decimal representation of 5/23 is a non-terminating, non-repeating decimal (an irrational number). Rounding is necessary to express it as a practical percentage value.
Q5: How can I improve my understanding of fraction-to-percentage conversions?
A5: Practice! Try converting various fractions to percentages. Start with simpler fractions and gradually increase the complexity. You can also find numerous online resources and practice exercises to help you.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. While the process might seem simple, understanding the underlying principles and the potential for approximation is essential. By mastering this skill, you'll equip yourself with a valuable tool for various calculations and analyses across diverse fields. Remember to practice regularly to build confidence and accuracy in your conversions. The step-by-step guide provided in this article, along with the clarification on approximations and the practical applications discussed, should empower you to confidently tackle similar fraction-to-percentage conversion problems in the future.
Latest Posts
Latest Posts
-
10 Yard Concrete Truck Cost
Sep 22, 2025
-
Square Root Of 28 Simplified
Sep 22, 2025
-
Can Fractions Be Rational Numbers
Sep 22, 2025
-
A Net For A Cylinder
Sep 22, 2025
-
Price Elasticity Of Demand Calculator
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 23 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.