5 6 Times 5 6
saludintensiva
Sep 13, 2025 · 5 min read
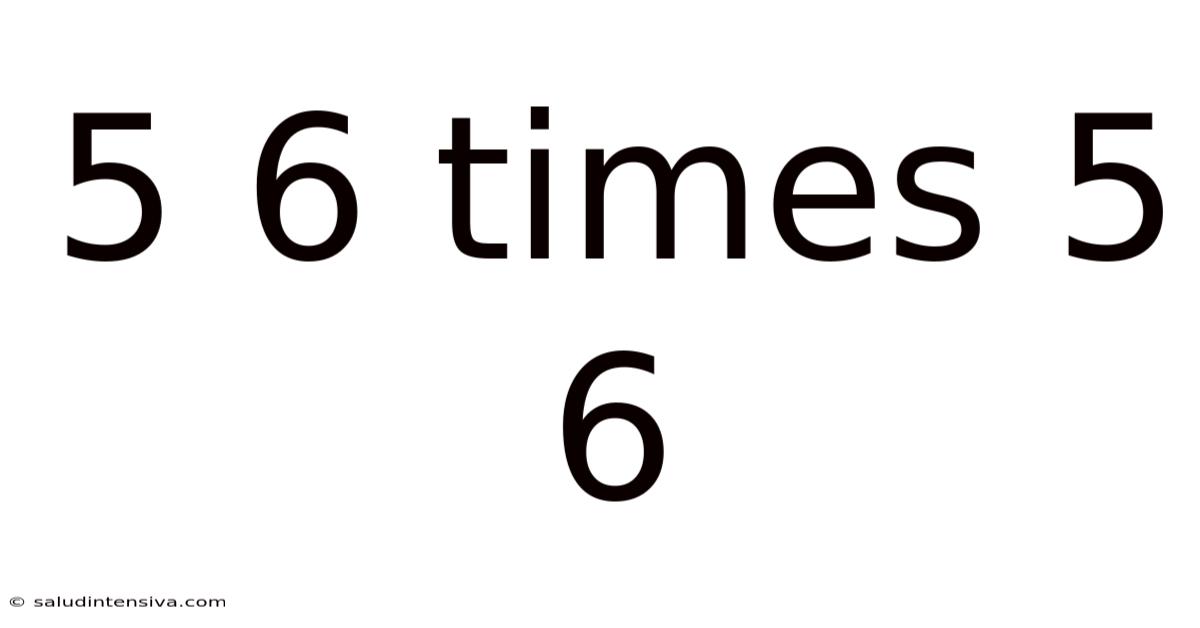
Table of Contents
Decoding the Mystery: 5.6 Times 5.6 and Beyond
Are you intrigued by the seemingly simple yet surprisingly complex calculation of 5.6 multiplied by 5.6? This seemingly straightforward multiplication problem opens doors to a deeper understanding of decimal multiplication, significant figures, and even the practical applications of these concepts in everyday life. This article will not only solve 5.6 x 5.6 but will also explore the underlying mathematical principles, provide different methods for solving the problem, and discuss the broader implications of decimal calculations.
Understanding Decimal Multiplication
Before we dive into solving 5.6 x 5.6, let's refresh our understanding of decimal multiplication. Decimals represent fractions where the denominator is a power of 10 (e.g., 10, 100, 1000, etc.). When multiplying decimals, we initially ignore the decimal points and multiply the numbers as if they were whole numbers. The crucial step comes after the multiplication: counting the total number of decimal places in the original numbers and placing the decimal point in the product accordingly.
For instance, multiplying 2.5 by 1.2:
- Ignore the decimal points: 25 x 12 = 300
- Count decimal places: 2.5 has one decimal place, and 1.2 has one decimal place, totaling two decimal places.
- Place the decimal point: Starting from the rightmost digit of the product (300), move the decimal point two places to the left, resulting in 3.00 or 3.
Method 1: Traditional Multiplication
This is the most common method taught in schools. We can break down 5.6 x 5.6 into a more manageable format:
5.6
x 5.6
-------
336 (5.6 x 6)
2800 (5.6 x 50)
-------
3136
Since both 5.6 and 5.6 have one decimal place each, the product will have two decimal places. Therefore, 5.6 x 5.6 = 31.36.
Method 2: Using the Distributive Property
The distributive property allows us to break down the multiplication into smaller, easier-to-manage parts:
5.6 x 5.6 = (5 + 0.6) x (5 + 0.6)
Applying the distributive property (FOIL method):
= (5 x 5) + (5 x 0.6) + (0.6 x 5) + (0.6 x 0.6) = 25 + 3 + 3 + 0.36 = 31.36
This method demonstrates a deeper understanding of the underlying mathematical principles and can be particularly useful for mental calculations with slightly more complex numbers.
Method 3: Conversion to Fractions
Decimals can be easily converted into fractions. This approach is helpful for visualizing the multiplication and understanding the concept of fractions.
5.6 can be written as 56/10. Therefore, the calculation becomes:
(56/10) x (56/10) = 3136/100 = 31.36
This method highlights the relationship between decimals and fractions, reinforcing fundamental mathematical concepts.
Method 4: Using a Calculator
In today's world, calculators are readily available. While understanding the underlying methods is crucial, using a calculator provides a quick and efficient way to verify the answer. Simply input 5.6 x 5.6 and the calculator will display 31.36.
Significance and Applications
The seemingly simple calculation of 5.6 x 5.6 has wide-ranging applications. Consider these examples:
-
Area Calculation: If you have a square plot of land measuring 5.6 meters on each side, the total area would be 5.6 x 5.6 = 31.36 square meters. This is a fundamental calculation in geometry and surveying.
-
Cost Calculation: If an item costs $5.60 and you buy 5.6 units, the total cost would be 5.6 x 5.6 = $31.36. This simple calculation is crucial for everyday budgeting and financial management.
-
Scientific Calculations: In scientific fields, decimal multiplications are integral to various calculations, including those related to measurements, conversions, and experimental data analysis. Accuracy is crucial, so understanding significant figures (discussed below) is especially important.
-
Engineering and Construction: Calculations involving dimensions, materials, and costs frequently involve decimal numbers. Accurate decimal multiplication ensures precise measurements and cost estimations, essential for successful projects.
Significant Figures and Rounding
When dealing with decimal numbers, particularly in scientific or engineering contexts, the concept of significant figures becomes important. Significant figures represent the number of digits in a value that contribute to its precision. The number 5.6 has two significant figures. When multiplying numbers, the result should not have more significant figures than the least precise number involved in the calculation.
In our case, 5.6 x 5.6 = 31.36. Since both numbers have two significant figures, the result should ideally also have two significant figures. However, rounding in this case would change the value significantly. Therefore, in this context, all four digits (31.36) are considered significant due to the direct nature of the calculation. However, understanding significant figures is critical when dealing with measurements or experimental data where rounding would appropriately reflect the precision of the measurements.
Frequently Asked Questions (FAQ)
-
What if I need to multiply 5.6 by a larger number? The same principles apply. You can use any of the methods mentioned above, breaking down the multiplication into smaller, manageable parts if necessary.
-
How can I improve my decimal multiplication skills? Practice is key! Start with simpler calculations and gradually increase the complexity. Understanding the underlying principles and using different methods will build your confidence and accuracy.
-
Are there other ways to solve 5.6 x 5.6? Yes, there are various advanced mathematical techniques, such as logarithms or using specialized software, but the methods outlined above are sufficient for most purposes.
-
What happens if I make a mistake in placing the decimal point? The result will be significantly incorrect, potentially leading to errors in calculations and real-world applications.
Conclusion
The calculation of 5.6 x 5.6, while seemingly trivial, offers a valuable opportunity to explore the fundamental principles of decimal multiplication and its widespread applications. Whether using traditional multiplication, the distributive property, or converting to fractions, mastering these techniques builds a strong foundation for more complex mathematical endeavors. Remember to consider significant figures when dealing with measured values to maintain accuracy and ensure the reliability of your calculations. By understanding the underlying concepts and practicing regularly, you can confidently tackle similar decimal multiplication problems and apply this knowledge to diverse real-world scenarios. The seemingly simple act of multiplying 5.6 by 5.6 opens a world of mathematical understanding and practical applications, enriching your problem-solving capabilities and enhancing your appreciation for the power of numbers.
Latest Posts
Latest Posts
-
Whats 625 As A Fraction
Sep 13, 2025
-
3 5 Out Of 5 Percentage
Sep 13, 2025
-
Solve 1 4 5 4
Sep 13, 2025
-
2 1 7 As Improper Fraction
Sep 13, 2025
-
0 23 Acres To Square Feet
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Times 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.