5 8/10 As A Decimal
saludintensiva
Sep 22, 2025 · 5 min read
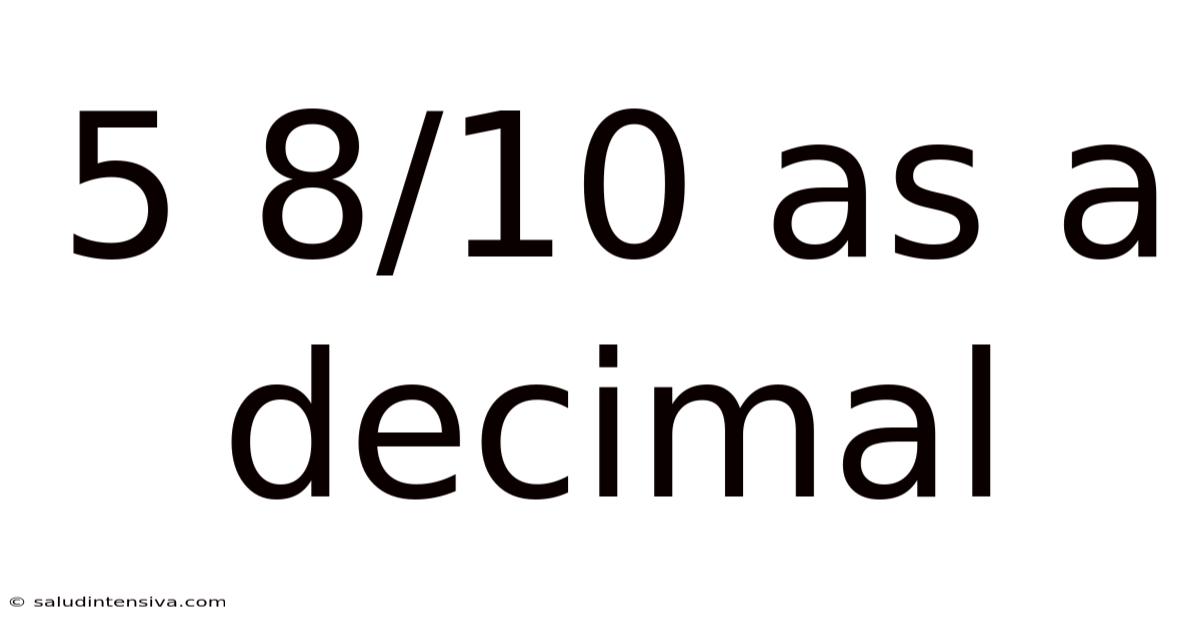
Table of Contents
Decoding 5 8/10 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the mixed number 5 8/10 into its decimal equivalent, explaining the underlying principles and providing practical examples. We'll also explore related concepts and answer frequently asked questions to solidify your understanding. This article covers the basics of fraction-to-decimal conversion, making it suitable for students, professionals, or anyone looking to refresh their mathematical skills.
Understanding Mixed Numbers and Fractions
Before we dive into the conversion, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 5 8/10. The whole number (5 in this case) represents a complete unit, while the fraction (8/10) represents a part of a unit. The fraction itself consists of a numerator (8, the top number) and a denominator (10, the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Converting 5 8/10 to a Decimal: A Step-by-Step Approach
Converting a mixed number like 5 8/10 to a decimal involves two main steps:
Step 1: Convert the Fraction to a Decimal
The core of the conversion lies in transforming the fraction 8/10 into a decimal. This is relatively straightforward because the denominator is a power of 10 (10¹). To convert a fraction to a decimal, we simply divide the numerator by the denominator:
8 ÷ 10 = 0.8
Therefore, the fraction 8/10 is equivalent to the decimal 0.8.
Step 2: Combine the Whole Number and the Decimal
Now that we have the decimal equivalent of the fraction, we simply combine it with the whole number part of the mixed number:
5 + 0.8 = 5.8
Therefore, the mixed number 5 8/10 is equivalent to the decimal 5.8.
Alternative Methods for Fraction to Decimal Conversion
While the method above is the most straightforward for fractions with denominators that are powers of 10, let's explore alternative approaches that work for fractions with other denominators.
Method 1: Long Division
This method is universally applicable for any fraction. You divide the numerator by the denominator using long division. For example, to convert 7/8 to a decimal, you would perform 7 ÷ 8. This will yield a decimal answer (0.875).
Method 2: Equivalent Fractions
If the denominator is not a power of 10, you can try to find an equivalent fraction with a denominator that is a power of 10. For example, to convert 3/4 to a decimal, we can find an equivalent fraction with a denominator of 100:
3/4 = (3 x 25) / (4 x 25) = 75/100 = 0.75
This method is only practical for fractions where finding an equivalent fraction with a power of 10 denominator is relatively easy.
Understanding Decimal Place Value
The decimal system uses place value to represent numbers. Each digit in a decimal number has a specific value based on its position relative to the decimal point. In the number 5.8, the digit 5 represents 5 ones, and the digit 8 represents 8 tenths (8/10). Understanding place value is crucial for comprehending the magnitude of decimal numbers and performing arithmetic operations.
For example:
- 5.8 The '5' is in the ones place, and the '8' is in the tenths place.
- 5.80 Adding a zero to the end doesn't change the value. It’s still 5 and 8/10. This is useful for aligning decimal numbers during addition and subtraction.
- 5.800 Similarly, adding more zeros to the right of the last non-zero digit doesn't alter the value.
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in various fields and everyday situations:
- Finance: Calculating percentages, interest rates, and discounts.
- Science: Measuring quantities, recording experimental data, and performing calculations.
- Engineering: Design, construction, and precision measurements.
- Cooking and Baking: Following recipes that require precise measurements.
- Everyday Calculations: Sharing items equally, calculating tips, or comparing prices.
Advanced Concepts: Recurring and Terminating Decimals
When converting fractions to decimals, you might encounter two types of decimals:
-
Terminating decimals: These decimals have a finite number of digits after the decimal point, like 0.75 or 0.8. They typically result from fractions where the denominator can be expressed as a product of 2s and 5s.
-
Recurring decimals (repeating decimals): These decimals have digits that repeat infinitely after the decimal point, like 1/3 = 0.333... or 1/7 = 0.142857142857... These often result from fractions with denominators that have prime factors other than 2 and 5. Recurring decimals are often represented using a bar over the repeating digits (e.g., 0.3̅).
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to decimals?
Yes, all fractions can be converted to decimals. However, the decimal representation may be terminating or recurring.
Q2: What if the denominator of my fraction is not a power of 10?
Use long division or try to find an equivalent fraction with a denominator that is a power of 10.
Q3: Why is understanding decimal conversion important?
Decimal conversion is vital for numerous applications in mathematics, science, finance, and everyday life, facilitating accurate calculations and comparisons.
Q4: How can I improve my understanding of fractions and decimals?
Practice converting fractions to decimals and vice versa. Use online resources, worksheets, and educational apps to reinforce your learning.
Conclusion
Converting the mixed number 5 8/10 to its decimal equivalent, 5.8, is a relatively simple process involving dividing the numerator of the fraction by the denominator and adding the result to the whole number. This skill is fundamental in mathematics and has wide-ranging practical applications. Understanding the underlying principles, alternative conversion methods, and the nature of terminating and recurring decimals will equip you with a solid foundation for tackling more complex mathematical problems. Remember that consistent practice is key to mastering this important skill. Through understanding the concepts presented here and engaging in regular practice, you can confidently navigate the world of fractions and decimals.
Latest Posts
Latest Posts
-
19 Degrees Fahrenheit To Celsius
Sep 22, 2025
-
Multiplying Decimals Using Area Models
Sep 22, 2025
-
How Much Is 21 Kg
Sep 22, 2025
-
4400 Meters Squared To Feet
Sep 22, 2025
-
What Is 3 5 Of 5
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 8/10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.