6 1/4 - 3 5/8
saludintensiva
Sep 19, 2025 · 6 min read
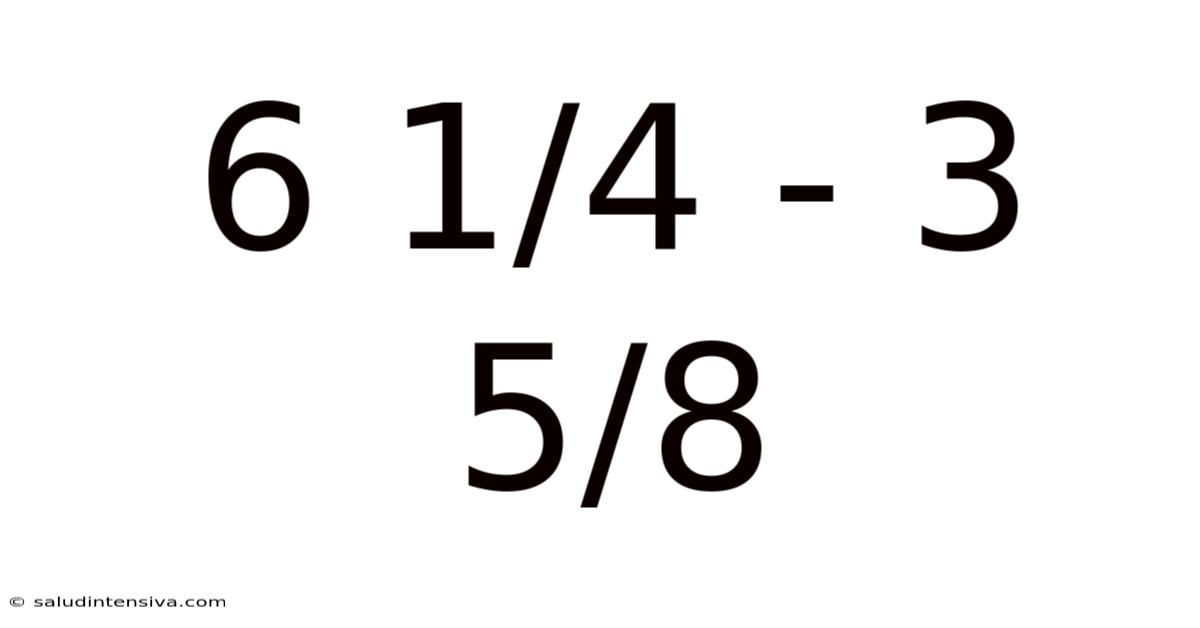
Table of Contents
Mastering Mixed Number Subtraction: A Deep Dive into 6 1/4 - 3 5/8
Understanding subtraction of mixed numbers is a crucial skill in mathematics, forming the foundation for more advanced concepts in algebra, calculus, and beyond. This comprehensive guide will walk you through solving the problem 6 1/4 - 3 5/8, explaining the process step-by-step, clarifying common pitfalls, and providing a deeper understanding of the underlying mathematical principles. This detailed explanation will be beneficial for students, educators, and anyone looking to refresh their knowledge of fraction subtraction.
Introduction: Understanding Mixed Numbers and the Problem
Before tackling the specific problem, let's refresh our understanding of mixed numbers. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 6 1/4 represents six whole units and one-quarter of a unit. The problem 6 1/4 - 3 5/8 requires us to subtract one mixed number from another. This involves understanding both fraction subtraction and the manipulation of whole numbers. The seemingly simple operation hides several nuances that we will unpack throughout this article.
Step-by-Step Solution: 6 1/4 - 3 5/8
The key to solving this problem lies in finding a common denominator for the fractions. This allows us to directly subtract the fractional parts.
-
Find a Common Denominator: The denominators of our fractions are 4 and 8. The least common multiple (LCM) of 4 and 8 is 8. We'll convert both fractions to have a denominator of 8.
-
Convert the Fractions:
- 1/4 can be converted to 2/8 (multiply both the numerator and denominator by 2).
- 5/8 remains as 5/8.
-
Rewrite the Problem: Our problem now becomes 6 2/8 - 3 5/8.
-
Address the Subtraction Issue: Notice that we cannot directly subtract 5/8 from 2/8; the result would be a negative fraction. This requires us to borrow from the whole number part.
-
Borrowing from the Whole Number: We borrow 1 from the whole number 6, leaving us with 5. This borrowed 1 is then expressed as a fraction with the common denominator (8/8).
-
Rewrite Again: The problem now transforms into (5 + 8/8) + 2/8 - 3 5/8, which simplifies to 5 10/8 - 3 5/8.
-
Subtract the Fractions: Now we can subtract the fractions: 10/8 - 5/8 = 5/8.
-
Subtract the Whole Numbers: Subtract the whole numbers: 5 - 3 = 2.
-
Combine the Results: Combining the results from steps 7 and 8, we get the final answer: 2 5/8.
Therefore, 6 1/4 - 3 5/8 = 2 5/8.
Explanation of the Borrowing Process: A Deeper Look
The borrowing process is a critical step often misunderstood. When we "borrow" 1 from the 6, we aren't just taking away a whole number; we're converting a whole unit into its fractional equivalent using the common denominator. This allows us to have enough fractional parts to perform the subtraction. This concept is fundamental to understanding operations with mixed numbers. Think of it like converting dollars to cents – you're changing the form but maintaining the same overall value.
Alternative Method: Converting to Improper Fractions
Another approach to solving this problem involves converting both mixed numbers into improper fractions (fractions where the numerator is greater than or equal to the denominator) before subtracting.
-
Convert to Improper Fractions:
- 6 1/4 = (6 * 4 + 1) / 4 = 25/4
- 3 5/8 = (3 * 8 + 5) / 8 = 29/8
-
Find a Common Denominator: The common denominator is still 8.
-
Convert to Equivalent Fractions: 25/4 is equivalent to 50/8 (multiply both numerator and denominator by 2).
-
Subtract the Fractions: 50/8 - 29/8 = 21/8
-
Convert Back to a Mixed Number: 21/8 can be expressed as a mixed number by dividing 21 by 8: 2 with a remainder of 5. This gives us 2 5/8.
This method, while slightly more complex initially, reinforces the fundamental principle of equivalent fractions and demonstrates that there are multiple paths to the correct solution.
Checking Your Work: Ensuring Accuracy
It's always a good practice to check your answer. One way to do this is to reverse the operation. Add your answer (2 5/8) to the subtracted number (3 5/8):
2 5/8 + 3 5/8 = 5 10/8
Since 10/8 simplifies to 1 2/8 (or 1 1/4), we have 5 10/8 = 6 2/8 = 6 1/4. This matches the original number we subtracted from, confirming our answer is correct.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when subtracting mixed numbers:
-
Forgetting to find a common denominator: This is the most frequent error. Always ensure your fractions have the same denominator before attempting subtraction.
-
Incorrect borrowing: Failing to borrow correctly or borrowing the wrong amount can lead to incorrect results. Carefully consider the fractional parts when borrowing.
-
Incorrect simplification: After subtracting, always simplify your answer to its lowest terms.
-
Ignoring the whole numbers: Remember to subtract the whole number parts as well.
Frequently Asked Questions (FAQs)
-
Q: Can I subtract mixed numbers without finding a common denominator? A: No, you must find a common denominator to subtract the fractional parts directly.
-
Q: What if the fractional part of the number I'm subtracting is larger? A: You will need to borrow from the whole number part, as demonstrated in the step-by-step solution.
-
Q: Can I use a calculator for this? A: While calculators can handle fraction operations, understanding the manual process is crucial for developing mathematical fluency. Calculators should be used to check your work, not replace the learning process.
-
Q: What are some real-world applications of this concept? A: Subtracting mixed numbers is used in various applications like measuring ingredients in cooking, calculating distances, and performing financial calculations.
Conclusion: Mastering Mixed Number Subtraction
Subtracting mixed numbers, as illustrated by the example 6 1/4 - 3 5/8, requires a systematic approach involving finding a common denominator, potentially borrowing from the whole number, and accurately performing both fractional and whole number subtraction. Understanding the underlying mathematical principles, such as the concept of borrowing and the importance of common denominators, is critical for success. By following the steps outlined in this guide and practicing consistently, you can master this important skill and build a strong foundation in mathematical operations. Remember, the key to success lies in understanding the why behind each step, not just memorizing the process. This deeper understanding will serve you well in tackling more advanced mathematical concepts in the future.
Latest Posts
Latest Posts
-
Word To Telephone Number Converter
Sep 19, 2025
-
Gcf Of 15 And 18
Sep 19, 2025
-
15 7 As A Mixed Number
Sep 19, 2025
-
Convert 175 Pounds To Kilograms
Sep 19, 2025
-
Is 5 6 Less Than 1 2
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 6 1/4 - 3 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.