Is 5/6 Less Than 1/2
saludintensiva
Sep 19, 2025 · 5 min read
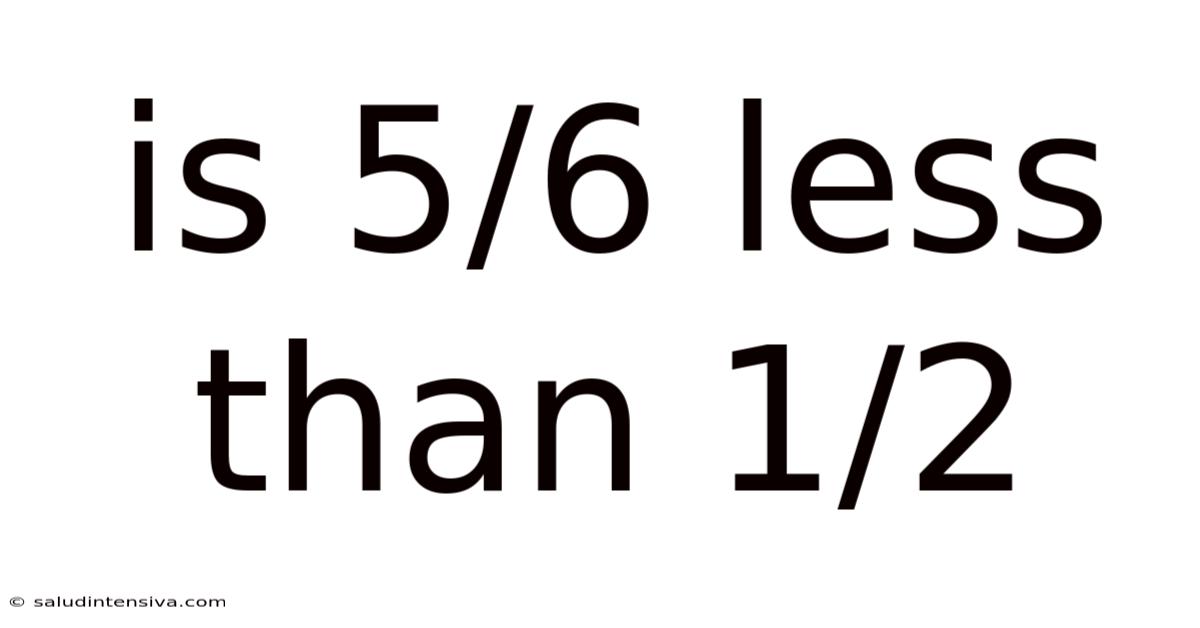
Table of Contents
Is 5/6 Less Than 1/2? A Deep Dive into Fraction Comparison
This article explores the question: "Is 5/6 less than 1/2?" While the answer might seem immediately obvious to some, a deeper understanding of fractions and their representation is crucial for mastering mathematical concepts. We'll not only answer the question definitively but also delve into the methods for comparing fractions, their practical applications, and address common misconceptions. This will equip you with the tools to confidently tackle similar fraction comparisons in the future.
Understanding Fractions: A Quick Refresher
Before we jump into comparing 5/6 and 1/2, let's briefly review what fractions represent. A fraction, like 5/6, consists of two parts:
- Numerator: The top number (5 in this case) represents the number of parts we have.
- Denominator: The bottom number (6 in this case) represents the total number of equal parts the whole is divided into.
Therefore, 5/6 means we have 5 out of 6 equal parts of a whole. Similarly, 1/2 means we have 1 out of 2 equal parts of a whole.
Method 1: Visual Representation
One of the easiest ways to compare fractions is through visual aids. Imagine two identical circles.
-
Representing 1/2: Divide the first circle into two equal halves. Shade one half. This visually represents 1/2.
-
Representing 5/6: Divide the second circle into six equal parts. Shade five of these parts. This visually represents 5/6.
By comparing the shaded areas, it becomes immediately apparent that the shaded area representing 5/6 is significantly larger than the shaded area representing 1/2. Therefore, 5/6 is greater than 1/2, not less.
Method 2: Finding a Common Denominator
A more rigorous mathematical approach involves finding a common denominator for both fractions. The common denominator is a number that is a multiple of both denominators (6 and 2 in this case). The least common multiple (LCM) of 6 and 2 is 6.
-
Converting 1/2: To convert 1/2 to have a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
Comparing the fractions: Now we can compare 5/6 and 3/6. Since 5 > 3, it follows that 5/6 > 3/6. Therefore, 5/6 is greater than 1/2.
Method 3: Decimal Conversion
Another approach is to convert both fractions into decimals. This method is particularly useful when dealing with more complex fractions.
-
Converting 5/6 to a decimal: Divide the numerator (5) by the denominator (6): 5 ÷ 6 ≈ 0.833
-
Converting 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
Comparing the decimal values, 0.833 > 0.5. Therefore, 5/6 is greater than 1/2.
Method 4: Cross-Multiplication
Cross-multiplication provides a direct method for comparing two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice-versa.
-
Cross-multiplying: Multiply 5 (numerator of 5/6) by 2 (denominator of 1/2): 5 x 2 = 10
-
Cross-multiplying: Multiply 1 (numerator of 1/2) by 6 (denominator of 5/6): 1 x 6 = 6
Since 10 > 6, the fraction with the larger result from the cross-multiplication (5/6) is the larger fraction. Therefore, 5/6 is greater than 1/2.
Addressing Common Misconceptions
A common mistake when comparing fractions is focusing solely on the numerators or denominators without considering the relationship between them. For example, some might incorrectly assume that because 5 (the numerator of 5/6) is greater than 1 (the numerator of 1/2), then 5/6 must be greater than 1/2. This is incorrect, as the denominators significantly impact the value of the fraction.
Practical Applications of Fraction Comparison
The ability to compare fractions isn't just a theoretical mathematical exercise; it has numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Following recipes often involves accurately measuring ingredients, which requires comparing fractions (e.g., determining if 1/4 cup is more or less than 2/3 cup).
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Comparing fractions is crucial to ensure accuracy in dimensions and proportions.
-
Finance and Budgeting: Managing personal finances involves working with fractions of money (e.g., comparing discounts or interest rates).
-
Data Analysis: Analyzing data frequently involves comparing proportions and percentages, which are essentially represented by fractions.
Frequently Asked Questions (FAQ)
Q: What if the fractions have different denominators and finding a common denominator seems difficult?
A: While finding a common denominator is often the most straightforward method, you can always use the decimal conversion or cross-multiplication methods, which work regardless of the denominators.
Q: Are there any shortcuts for comparing fractions with large numbers?
A: For very large numbers, converting to decimals might be more efficient than finding a common denominator. Using a calculator can streamline the process.
Q: Can I compare fractions with negative numbers?
A: Yes, the same methods apply. Remember that a larger negative number is actually smaller than a smaller negative number (e.g., -5/6 is greater than -1/2).
Q: What if one fraction is a mixed number (e.g., 1 1/2)?
A: First, convert the mixed number into an improper fraction. For example, 1 1/2 is equivalent to 3/2. Then, use any of the methods described above to compare it to the other fraction.
Conclusion
In conclusion, 5/6 is definitively greater than 1/2. This article has explored multiple methods for comparing fractions – visual representation, common denominator, decimal conversion, and cross-multiplication – providing a comprehensive understanding of the process. Understanding fraction comparison is a fundamental skill with broad applications, extending beyond the classroom into numerous aspects of daily life and professional fields. Mastering these techniques equips you to tackle fraction-related problems with confidence and accuracy. Remember to choose the method that feels most comfortable and efficient for you, depending on the complexity of the fractions involved. Practice is key to solidifying your understanding and developing fluency in working with fractions.
Latest Posts
Latest Posts
-
5 And A Half Inches
Sep 19, 2025
-
Gcf Of 50 And 8
Sep 19, 2025
-
6 1 4 In Decimal
Sep 19, 2025
-
1 11 As A Percent
Sep 19, 2025
-
21 16 As A Mixed Number
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 5/6 Less Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.