6 10 As A Percent
saludintensiva
Sep 16, 2025 · 5 min read
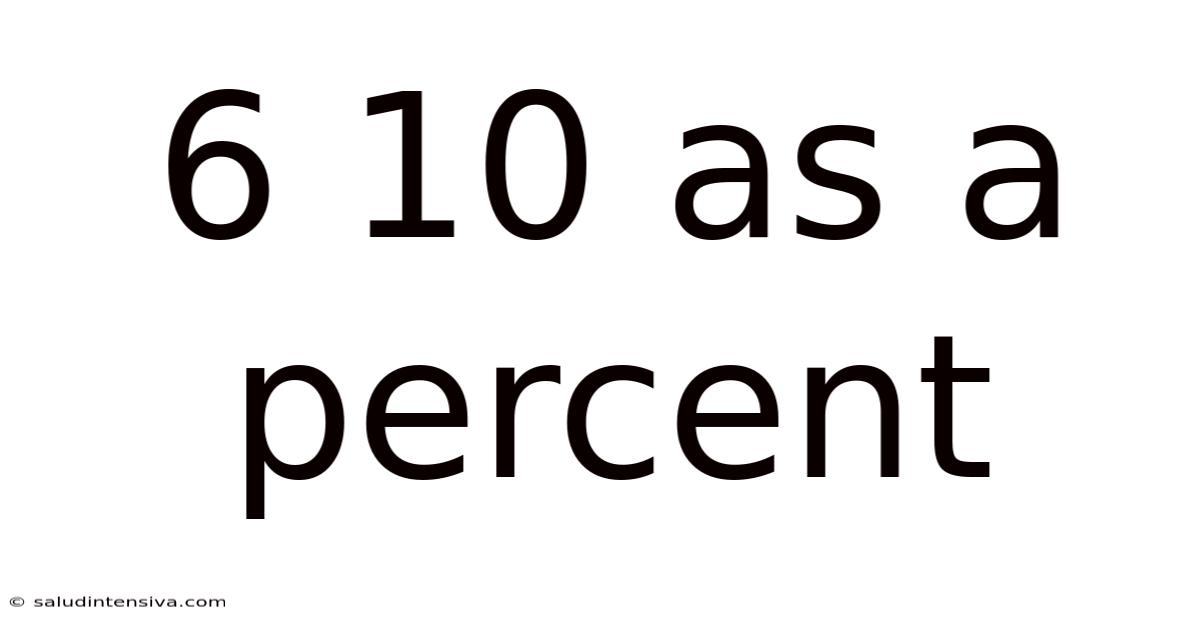
Table of Contents
6/10 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from everyday budgeting to advanced scientific calculations. This comprehensive guide will delve into the process of converting the fraction 6/10 into a percentage, explaining the methodology in detail and offering insights into the broader concept of fraction-to-percentage conversion. We'll explore different methods, address common misconceptions, and provide practical examples to solidify your understanding. By the end, you'll not only know that 6/10 is equal to 60%, but you'll also possess the tools to tackle similar conversions with confidence.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 6/10, 6 is the numerator and 10 is the denominator. This signifies that we're considering 6 parts out of a total of 10 parts.
A percentage, on the other hand, represents a fraction out of 100. The term "percent" literally means "per hundred." So, 60% signifies 60 parts out of 100. Understanding this fundamental relationship is key to converting between fractions and percentages.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage involves two simple steps:
-
Divide the numerator by the denominator: In our case, we divide 6 by 10: 6 ÷ 10 = 0.6
-
Multiply the result by 100: This converts the decimal to a percentage. 0.6 × 100 = 60
Therefore, 6/10 is equal to 60%.
Method 2: Simplifying the Fraction First
Sometimes, simplifying the fraction before conversion can make the calculation easier. In this case, 6/10 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
6 ÷ 2 = 3 10 ÷ 2 = 5
This simplifies the fraction to 3/5. Now, we can apply the same steps as Method 1:
-
Divide the numerator by the denominator: 3 ÷ 5 = 0.6
-
Multiply the result by 100: 0.6 × 100 = 60
Again, we arrive at the answer: 6/10 = 60%. This method highlights the equivalence of fractions – simplifying a fraction doesn't change its value, only its representation.
Method 3: Using Proportions
This method is particularly useful for visualizing the conversion. We set up a proportion where the fraction is equal to a percentage over 100:
6/10 = x/100
To solve for x (the percentage), we can cross-multiply:
10x = 600
Then, divide both sides by 10:
x = 60
Thus, 6/10 = 60%. This method emphasizes the inherent relationship between fractions and percentages as equivalent ratios.
Visualizing 6/10 as 60%
Imagine a pizza cut into 10 equal slices. If you eat 6 slices, you've consumed 6/10 of the pizza. This is visually equivalent to 60 out of 100 slices if the pizza were cut into 100 slices. This visual representation reinforces the understanding of the equivalence between 6/10 and 60%.
Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages has widespread applications across various disciplines:
-
Finance: Calculating interest rates, discounts, and profit margins often requires converting fractions to percentages. For example, a 1/4 discount is equivalent to a 25% discount.
-
Statistics: Representing data using percentages makes it easier to interpret and compare results. For instance, if 3 out of 5 students passed an exam (3/5), this translates to a 60% pass rate.
-
Science: Expressing experimental results as percentages provides a standardized and easily understood way to communicate findings.
-
Everyday Life: Calculating tips, sales tax, and understanding proportions in recipes all involve converting fractions to percentages.
Common Misconceptions and Troubleshooting
-
Incorrect placement of the decimal point: A common mistake is misplacing the decimal point when multiplying by 100. Remember to move the decimal point two places to the right.
-
Forgetting to multiply by 100: Remember that the final step in the conversion is crucial; multiplying by 100 transforms the decimal into a percentage.
-
Difficulty simplifying fractions: Practice simplifying fractions to make the conversion process more efficient. If you struggle with simplifying, brush up on your greatest common divisor (GCD) skills.
-
Confusing numerator and denominator: Always ensure you correctly identify the numerator (the part) and the denominator (the whole) of the fraction.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: The same methods apply. The resulting percentage will be greater than 100%. For example, 11/10 converts to 110%.
Q: What if the fraction has a decimal in the numerator or denominator?
A: You can still use the division method; just perform the division as usual. For example, 2.5/5 = 0.5, which is 50%.
Q: Are there any online calculators that can help with this conversion?
A: Yes, many online calculators can perform this conversion quickly and easily. However, understanding the underlying principles is essential for applying this knowledge in different contexts.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. By understanding the different methods outlined—direct division, simplifying first, and using proportions—you can confidently convert any fraction to its percentage equivalent. Remember the crucial steps: divide the numerator by the denominator and then multiply by 100. Practice regularly, and you'll master this skill, paving the way for a deeper understanding of mathematical concepts and their real-world applications. The simple conversion of 6/10 to 60% serves as a foundational building block for more complex calculations and problem-solving. Remember to visualize the process, understand the underlying principles, and practice regularly to build your confidence and proficiency.
Latest Posts
Latest Posts
-
Lcm Of 24 And 8
Sep 16, 2025
-
1 3 As A Whole Number
Sep 16, 2025
-
Is 1 8 Bigger Than 3 16
Sep 16, 2025
-
Printable Military Time Conversion Chart
Sep 16, 2025
-
Half Of 1 2 Inch
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 6 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.