6 100 As A Percent
saludintensiva
Sep 13, 2025 · 5 min read
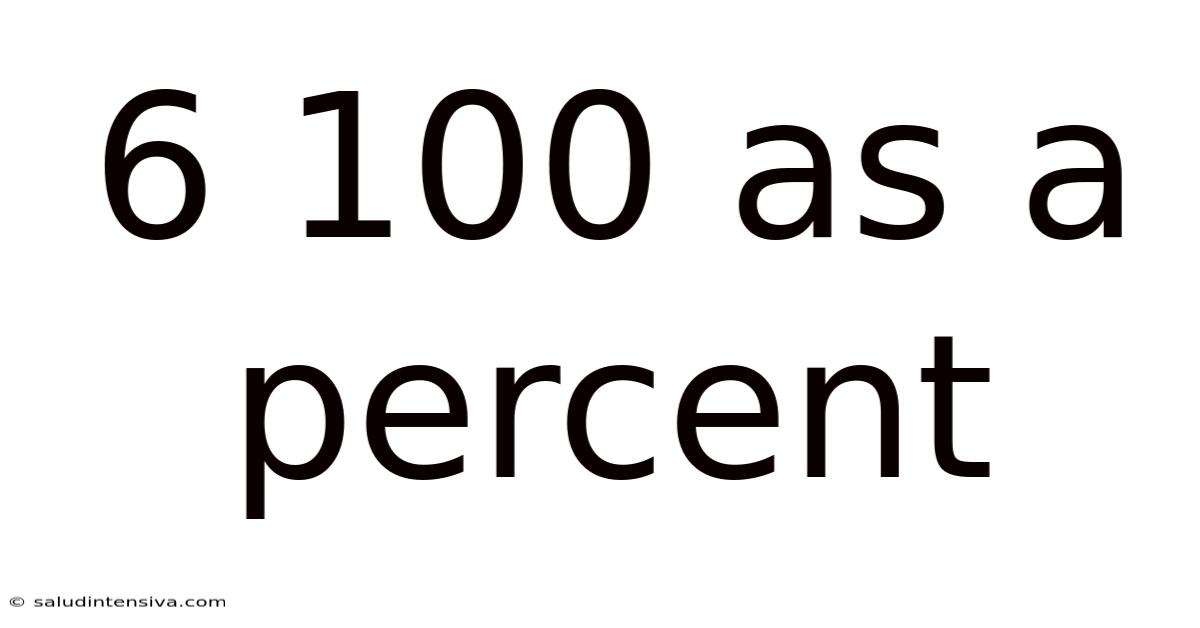
Table of Contents
6/100 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics and has wide-ranging applications in everyday life, from calculating discounts and taxes to interpreting data and statistics. This article will thoroughly explore how to express the fraction 6/100 as a percentage, explaining the underlying concepts and providing examples to solidify your understanding. We'll also delve into practical applications and address frequently asked questions.
Introduction: The Interplay of Fractions, Decimals, and Percentages
Before diving into the specific calculation of 6/100 as a percent, let's establish a clear understanding of these three interconnected concepts.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered. For example, 6/100 means 6 out of 100 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For instance, 0.06 represents six hundredths.
-
Percentages: Percentages express a fraction or decimal as a portion of 100. The symbol "%" represents "per cent," meaning "out of 100." Thus, a percentage indicates how many parts out of 100 are being considered.
These three concepts are interchangeable. You can convert a fraction to a decimal and then to a percentage, or vice versa. Understanding these conversions is crucial for solving various mathematical problems.
Converting 6/100 to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert 6/100 to a decimal, simply divide the numerator (6) by the denominator (100):
6 ÷ 100 = 0.06
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.06 × 100 = 6%
Therefore, 6/100 is equal to 6%.
Understanding the Concept: Why Multiply by 100?
The reason we multiply by 100 when converting a decimal to a percentage stems from the very definition of percentage: "per cent" means "out of 100." Multiplying by 100 essentially scales the decimal to represent its value as a proportion of 100.
For example, 0.06 represents 6 hundredths. Multiplying 0.06 by 100 gives us 6, signifying 6 out of 100, or 6%.
Practical Applications of Percentage Calculations
The ability to convert fractions and decimals to percentages is vital in numerous real-world situations. Here are some examples:
-
Calculating Discounts: A store offers a 20% discount on an item. To determine the discount amount, you would convert 20% to a decimal (0.20) and multiply it by the item's original price.
-
Determining Tax Rates: Sales tax is usually expressed as a percentage. To calculate the tax amount, you convert the tax rate (e.g., 6%) to a decimal (0.06) and multiply it by the price of the goods or services.
-
Interpreting Statistics: Many statistical reports present data as percentages. Understanding these percentages allows you to analyze trends, make comparisons, and draw meaningful conclusions.
-
Financial Calculations: Percentages are used extensively in finance, including calculating interest rates, returns on investments, and loan repayments.
-
Grade Calculation: Your final grade in a course is often expressed as a percentage, reflecting your performance compared to the total possible points.
Beyond 6/100: Working with Other Fractions and Percentages
The process of converting fractions to percentages is not limited to 6/100. The same steps apply to any fraction:
- Divide the numerator by the denominator to obtain the decimal equivalent.
- Multiply the decimal by 100 to obtain the percentage.
For example, let's convert 3/4 to a percentage:
- 3 ÷ 4 = 0.75
- 0.75 × 100 = 75%
Therefore, 3/4 is equal to 75%.
Converting Percentages to Fractions and Decimals
The conversion process also works in reverse. To convert a percentage to a fraction or decimal:
- To convert a percentage to a decimal, divide the percentage by 100. For example, 25% ÷ 100 = 0.25
- To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100, then simplify. For example, 25% = 25/100 = 1/4
Advanced Applications and Considerations
While converting 6/100 to a percentage is straightforward, more complex scenarios may involve:
- Percentages greater than 100%: These represent values exceeding the whole. For example, 150% represents 1.5 times the original value.
- Percentages involving multiple operations: Problems may require multiple steps, such as calculating a percentage increase or decrease followed by another percentage calculation.
- Understanding percentage change: This involves calculating the percentage difference between two values. The formula is: [(New Value - Old Value) / Old Value] x 100%.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 6/100?
A1: The simplest form of 6/100 is 3/50. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 2.
Q2: Can I convert a fraction with a denominator other than 100 directly to a percentage?
A2: Yes, you can. You can still divide the numerator by the denominator to get the decimal and then multiply by 100 to find the percentage.
Q3: How do I calculate a percentage increase?
A3: To calculate a percentage increase, find the difference between the new value and the original value, divide that difference by the original value, and then multiply by 100.
Q4: How do I calculate a percentage decrease?
A4: The process is similar to a percentage increase, but the result will be negative, indicating a decrease. Use the formula: [(Original Value - New Value) / Original Value] x 100%.
Conclusion: Mastering the Fundamentals of Percentages
Understanding how to express 6/100 as a percentage—and mastering the broader concepts of fractions, decimals, and percentages—is a fundamental skill with far-reaching applications. By grasping the principles of conversion and practicing different scenarios, you'll equip yourself with a valuable tool for navigating various mathematical and real-world challenges. Remember, the key lies in understanding the interconnectedness of these concepts and applying the appropriate conversion techniques consistently. From calculating discounts to interpreting statistical data, the ability to work comfortably with percentages will significantly enhance your quantitative reasoning skills.
Latest Posts
Latest Posts
-
Factors Of 10 In Pairs
Sep 13, 2025
-
What Are The Factors 20
Sep 13, 2025
-
Lcm For 18 And 30
Sep 13, 2025
-
Ti 84 Graphing Calculator Online
Sep 13, 2025
-
Is 2 3 Greater Than 2 5
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.