Lcm For 18 And 30
saludintensiva
Sep 13, 2025 · 6 min read
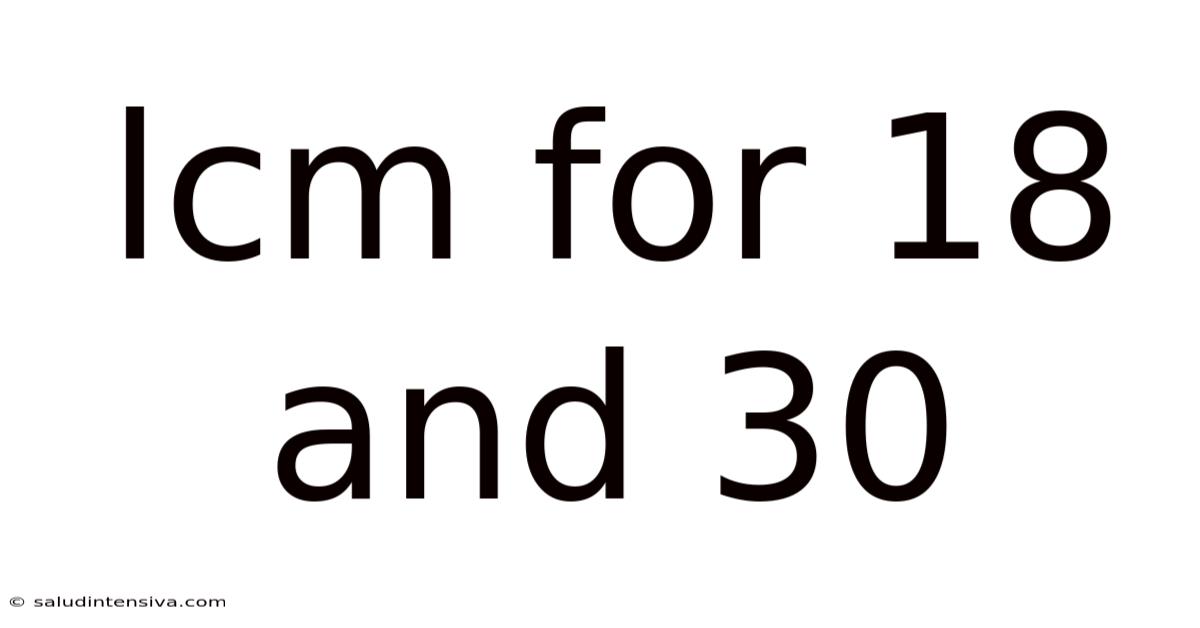
Table of Contents
Finding the Least Common Multiple (LCM) of 18 and 30: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 18 and 30, might seem like a simple arithmetic problem. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for grasping more advanced mathematical ideas. This article provides a comprehensive guide to finding the LCM of 18 and 30, exploring various approaches and delving into the mathematical principles involved. We'll move beyond simply providing the answer and explore the why behind the calculations, making this concept accessible to everyone, from beginners to those looking to refresh their mathematical skills.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. This concept is fundamental in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra.
Understanding LCM is vital in real-world scenarios. Imagine you're organizing a party, and you need to buy enough snacks for 18 guests and enough drinks for 30 guests. The LCM would tell you the smallest number of snack and drink packages you need to buy so that you have enough for each guest, without any leftovers.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of smaller numbers like 18 and 30 is by listing their multiples.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, ...
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, ...
By comparing the lists, we can identify the smallest number that appears in both lists: 90. Therefore, the LCM of 18 and 30 is 90.
This method is simple for smaller numbers, but it becomes cumbersome and impractical for larger numbers. It's important to understand this method as it builds foundational understanding, but it's not the most efficient for larger numbers.
Method 2: Prime Factorization
A more efficient and robust method, especially for larger numbers, involves using prime factorization. This method relies on breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Prime Factorization of 18: 18 = 2 × 9 = 2 × 3 × 3 = 2 × 3²
-
Prime Factorization of 30: 30 = 2 × 15 = 2 × 3 × 5
-
Finding the LCM using Prime Factors: To find the LCM, we take the highest power of each prime factor present in the factorizations of both numbers.
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ (from both 18 and 30).
- The highest power of 3 is 3² (from 18).
- The highest power of 5 is 5¹ (from 30).
-
Calculating the LCM: Multiply the highest powers of each prime factor together:
LCM(18, 30) = 2¹ × 3² × 5¹ = 2 × 9 × 5 = 90
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or finding the LCM of more than two numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where:
- a and b are the two integers.
- |a × b| represents the absolute value of the product of a and b.
-
Finding the GCD of 18 and 30: We can use the Euclidean algorithm to find the GCD:
- Divide the larger number (30) by the smaller number (18): 30 ÷ 18 = 1 with a remainder of 12.
- Replace the larger number with the remainder (12) and repeat: 18 ÷ 12 = 1 with a remainder of 6.
- Repeat: 12 ÷ 6 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 6.
-
Calculating the LCM using the GCD:
LCM(18, 30) = (18 × 30) / 6 = 540 / 6 = 90
This method provides an alternative approach, particularly useful when you already know or can easily calculate the GCD of the two numbers. The Euclidean algorithm is a very efficient method for finding the GCD, even for large numbers.
Explaining the Mathematics Behind LCM
The concept of LCM is deeply rooted in number theory. Understanding prime factorization is crucial. When we break down numbers into their prime factors, we're essentially revealing their fundamental building blocks. The LCM represents the smallest number that contains all the building blocks of both (or all) the numbers involved. This is why the prime factorization method is so effective—it directly addresses the fundamental composition of the numbers. The relationship between the LCM and GCD further highlights the interconnectedness of these concepts within number theory.
Applications of LCM in Real-World Scenarios
Beyond the party snack example, the LCM has practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a station at different intervals. The LCM helps determine when both buses will arrive at the station simultaneously.
-
Manufacturing: In manufacturing processes, LCM can be used to coordinate the production cycles of different machines to optimize efficiency.
-
Music: In music theory, the LCM is used to determine the least common multiple of the durations of notes, allowing for a harmonious and balanced composition.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two numbers? A: The same principles apply. You can extend the prime factorization method or use iterative application of the GCD method to find the LCM of multiple numbers.
-
Q: Is there a way to find the LCM without prime factorization? A: While prime factorization is generally the most efficient, you can use the listing multiples method (though less practical for large numbers) or the GCD method.
-
Q: What is the difference between LCM and GCD? A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They represent opposite ends of the divisibility spectrum.
-
Q: Is the LCM always larger than the numbers themselves? A: Yes, unless one of the numbers is a multiple of the other. For example, the LCM of 6 and 12 is 12.
Conclusion: Mastering the LCM
Finding the LCM of 18 and 30, or any pair of numbers, involves more than just a simple calculation. It's about understanding the underlying mathematical principles and choosing the most appropriate method for the given situation. While the listing multiples method offers a basic understanding, prime factorization and the GCD method are significantly more efficient and provide a deeper appreciation of the mathematical concepts involved. Mastering LCM not only enhances your arithmetic skills but also strengthens your understanding of number theory and its application in various real-world scenarios. Remember that the key to success lies in choosing the right tool for the job—and understanding the why behind the calculations as much as the how.
Latest Posts
Latest Posts
-
3 1 5 As A Decimal
Sep 13, 2025
-
1900 Sq Ft To M2
Sep 13, 2025
-
Is 1 2 Equivalent To 2 4
Sep 13, 2025
-
Equivalent Fractions For 5 7
Sep 13, 2025
-
48 Grados Fahrenheit A Centigrados
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 18 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.