6 14 As A Percent
saludintensiva
Sep 13, 2025 · 5 min read
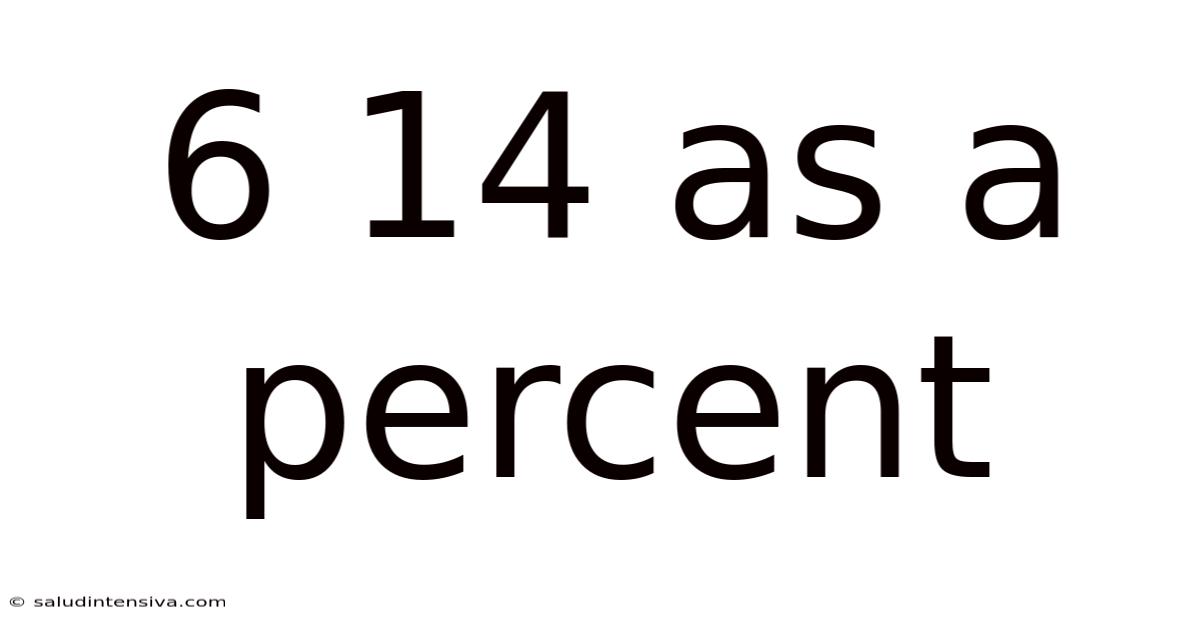
Table of Contents
Understanding 6/14 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 6/14 into a percentage, exploring the underlying concepts and providing practical examples. We will also address common misconceptions and offer advanced applications to solidify your understanding.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the conversion of 6/14, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 6/14 represents 6 parts out of a total of 14 parts.
-
Decimals: Represent a part of a whole using the base-10 number system. Decimals are expressed using a decimal point, separating the whole number from the fractional part.
-
Percentages: Express a part of a whole as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100."
These three forms are interchangeable, and the ability to convert between them is crucial for various mathematical applications.
Step-by-Step Conversion of 6/14 to a Percentage
The conversion of 6/14 to a percentage involves two main steps:
Step 1: Simplify the Fraction (if possible)
The first step is to simplify the fraction 6/14. Both the numerator (6) and the denominator (14) are divisible by 2. Simplifying gives us:
6/14 = 3/7
Simplifying the fraction makes the subsequent calculations easier and provides a more concise representation of the value.
Step 2: Convert the Simplified Fraction to a Decimal
To convert the simplified fraction 3/7 to a decimal, we divide the numerator (3) by the denominator (7):
3 ÷ 7 ≈ 0.42857
The result is an approximate decimal value because the division results in a repeating decimal. We can round this to a certain number of decimal places depending on the required level of accuracy. For this example, we'll use four decimal places: 0.4286.
Step 3: Convert the Decimal to a Percentage
To convert the decimal 0.4286 to a percentage, we multiply it by 100 and add the percentage symbol (%):
0.4286 × 100 = 42.86%
Therefore, 6/14 is approximately equal to 42.86%.
Explanation of the Mathematical Principles
The conversion from fraction to percentage relies on the fundamental principle that a percentage is a fraction with a denominator of 100. By dividing the numerator by the denominator, we find the decimal equivalent of the fraction. Multiplying this decimal by 100 then expresses the fraction as parts per hundred, which is the definition of a percentage. The process involves understanding the relationship between parts and wholes, and the ability to manipulate numerical representations.
Practical Applications and Real-World Examples
Understanding how to convert fractions to percentages is valuable in a wide range of situations:
-
Discounts: If a store offers a 6/14 discount on an item, this translates to a 42.86% discount.
-
Financial Analysis: Analyzing financial statements often involves working with fractions and percentages to understand ratios and proportions. For example, understanding the percentage of a company's revenue derived from a particular product line.
-
Statistics and Probability: Percentages are frequently used to express probabilities and statistical data. For example, the probability of an event occurring might be expressed as a percentage.
-
Scientific Measurements: Percentages are used to represent concentrations, error margins, and other aspects of scientific measurements.
-
Everyday Calculations: Calculating tips in restaurants, determining sale prices, and understanding interest rates all involve working with percentages.
Addressing Common Misconceptions
A common misconception is that simply multiplying the numerator by 100 will give the percentage. This is incorrect. The crucial step is to first divide the numerator by the denominator to obtain the decimal equivalent, and then multiply by 100 to get the percentage. Failing to perform the division leads to an incorrect result. Another misconception is believing that percentages always have to be whole numbers. As seen in the case of 6/14, the resulting percentage may contain decimal places.
Frequently Asked Questions (FAQ)
-
Q: Can I convert 6/14 to a percentage without simplifying the fraction?
- A: Yes, you can. However, simplifying the fraction makes the calculations easier and less prone to errors. The result will be the same regardless.
-
Q: What if I need a more precise percentage than 42.86%?
- A: You can use more decimal places in your calculations (e.g., 42.8571%). The level of precision needed depends on the context.
-
Q: Why is the decimal 0.42857 a repeating decimal?
- A: It's because the denominator (7) is not a factor of 10 or any power of 10. When a fraction's denominator contains prime factors other than 2 and 5, the decimal representation will be a repeating or non-terminating decimal.
Conclusion: Mastering Percentage Conversions
The ability to convert fractions to percentages is an essential mathematical skill. Understanding the steps involved, the underlying principles, and the practical applications empowers you to confidently handle a wide range of calculations in various contexts. Remember the key steps: simplify the fraction, convert to a decimal by division, and then multiply by 100 to obtain the percentage. This comprehensive guide provides a solid foundation for mastering this fundamental skill. By consistently practicing these conversions, you'll build confidence and proficiency in handling numerical representations and solving real-world problems that involve fractions and percentages. From simple daily calculations to complex financial analysis, this skillset is invaluable.
Latest Posts
Latest Posts
-
7 Percent Of 30 Hourrs
Sep 13, 2025
-
Solve E Mc2 For C
Sep 13, 2025
-
Boat Fuel Tank Size Calculator
Sep 13, 2025
-
70 Degrees Farenheit To Celcius
Sep 13, 2025
-
How Many Pounds 15 Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 14 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.