Solve E Mc2 For C
saludintensiva
Sep 13, 2025 · 6 min read
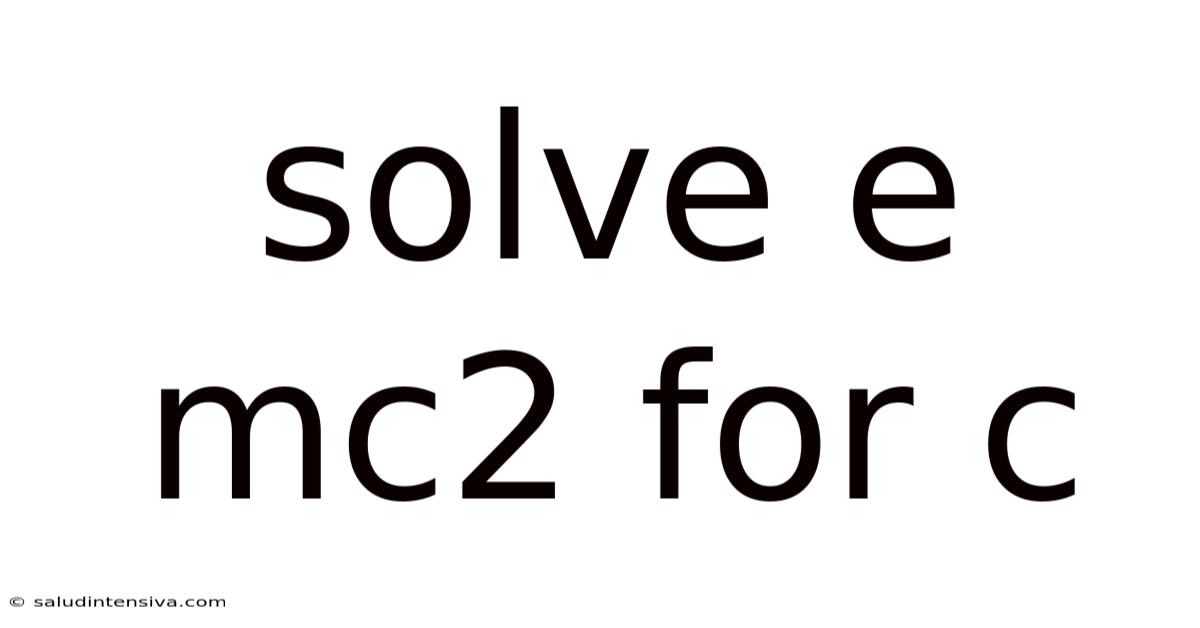
Table of Contents
Solving E=mc² for c: Unveiling the Speed of Light
Einstein's famous equation, E=mc², is arguably the most recognizable formula in all of physics. It elegantly describes the equivalence of energy (E) and mass (m), connected by the speed of light (c) squared. While the equation is celebrated for its simplicity, understanding its implications and manipulating it algebraically can be surprisingly insightful. This article will delve into the process of solving E=mc² for c, exploring the mathematical steps involved and unpacking the profound meaning behind the result. We'll also examine some real-world applications and address frequently asked questions.
Understanding the Equation: E=mc²
Before we embark on solving for c, let's briefly recap the meaning of each component in Einstein's equation:
-
E represents energy, typically measured in joules (J). Energy encompasses various forms, including kinetic energy (energy of motion), potential energy (stored energy), and rest energy (energy inherent to an object's mass).
-
m represents mass, usually measured in kilograms (kg). Mass is a measure of an object's resistance to acceleration. Crucially, Einstein's equation reveals that mass itself is a form of energy.
-
c represents the speed of light in a vacuum, a fundamental constant in physics, approximately 299,792,458 meters per second (m/s). It's a constant that sets a universal speed limit for information and energy transfer.
The equation E=mc² states that a small amount of mass can be converted into an enormous amount of energy, as the speed of light squared (c²) is a very large number. This principle underpins nuclear reactions, like those occurring in the sun and nuclear power plants.
Solving E=mc² for c: A Step-by-Step Guide
Solving for 'c' involves isolating it on one side of the equation using basic algebraic manipulation. Here's a breakdown of the process:
-
Start with the original equation: E = mc²
-
Divide both sides by 'm': To isolate c², we need to eliminate 'm' from the right side. We achieve this by dividing both sides of the equation by 'm'. This gives us:
E/m = c²
-
Take the square root of both sides: Now, we have c² on the right side. To find 'c', we take the square root of both sides of the equation:
√(E/m) = √c²
-
Simplify: The square root of c² is simply c. Therefore, our final solution is:
c = √(E/m)
This equation now allows us to calculate the speed of light (c) if we know the energy (E) and mass (m) involved in a system. It's important to remember that this calculation is only valid within the framework of special relativity and applies to systems where significant mass-energy conversion occurs.
The Significance of the Result: c = √(E/m)
The derived equation, c = √(E/m), offers several profound insights:
-
The speed of light as a fundamental constant: The equation reinforces the speed of light's role as a fundamental constant in the universe. It's not merely a property of light itself, but a universal constant that links energy and mass.
-
Mass-energy equivalence: The equation explicitly demonstrates the equivalence of energy and mass. A change in one directly impacts the other. This has significant implications in nuclear physics and our understanding of the universe's energy balance.
-
Predicting energy release: Knowing the mass lost (or converted into energy) during a process (like nuclear fission or fusion), we can predict the amount of energy released using this formula.
-
Limitations of classical physics: The equation highlights the limitations of classical Newtonian physics. It shows that concepts like mass and energy are not entirely separate but are intertwined in a profound way, revealed only by the theory of relativity.
Real-World Applications of E=mc² and its Solved Form
The implications of E=mc², and our ability to solve for c, are far-reaching, extending beyond theoretical physics:
-
Nuclear Power Generation: Nuclear power plants harness the energy released during nuclear fission, the splitting of atomic nuclei. The energy released is a direct consequence of the mass-energy equivalence, with a small fraction of mass converted into a substantial amount of energy.
-
Nuclear Weapons: The devastating power of nuclear weapons is a stark demonstration of E=mc². The immense energy released in a nuclear explosion stems from the conversion of a tiny fraction of the weapon's mass into energy.
-
Stellar Nucleosynthesis: The energy that powers stars, including our Sun, comes from nuclear fusion, where lighter atomic nuclei combine to form heavier ones. This process involves a mass deficit, with some mass converted into energy that keeps stars shining.
-
Particle Physics: In particle accelerators, particles are accelerated to extremely high speeds, resulting in significant increases in their energy. The relationship between energy and mass, governed by E=mc², is crucial for understanding the behavior and creation of new particles.
-
Medical Imaging: Techniques like PET (positron emission tomography) scans rely on the annihilation of positrons (antimatter electrons) with electrons, producing gamma rays. The energy of these gamma rays is directly related to the mass of the annihilated particles, demonstrating mass-energy conversion in a practical application.
Frequently Asked Questions (FAQ)
Q: Can we use E=mc² to explain everyday energy transformations, like burning wood?
A: While E=mc² governs all energy transformations, its impact is most pronounced in processes involving significant mass-energy conversions, such as nuclear reactions. In chemical reactions like burning wood, the mass change is extremely small and difficult to measure directly, rendering E=mc² less practical for calculations than other thermodynamic principles.
Q: Is the speed of light (c) truly constant, or are there situations where it changes?
A: The speed of light in a vacuum is a fundamental constant in our current understanding of physics. However, the speed of light can appear slower when traveling through a medium (like water or glass) due to interactions with the medium's particles. This apparent slowing down is a change in the phase velocity of light, not a change in the fundamental speed of light in a vacuum.
Q: Why is 'c' squared in the equation?
A: The square term (c²) reflects the magnitude of the energy released during mass-energy conversion. Because c is such a large number (approximately 3 x 10⁸ m/s), squaring it dramatically amplifies the effect of even a small mass change.
Q: Can we create matter from energy?
A: Yes, in principle, this is possible. The equation shows that energy can be converted into mass, and this has been demonstrated in particle physics experiments where high-energy collisions produce new particles. However, this process requires incredibly high energy densities.
Q: What are the units used in the E=mc² equation?
A: The common units are joules (J) for energy (E), kilograms (kg) for mass (m), and meters per second (m/s) for the speed of light (c).
Conclusion: A Timeless Equation and its Profound Implications
Einstein's E=mc² remains one of the most profound and influential equations in physics. Solving it for c = √(E/m) provides a powerful tool for understanding the fundamental relationship between energy and mass. The equation's simplicity belies its far-reaching implications, impacting our understanding of the universe's workings and inspiring numerous technological advancements. From the power of the stars to the development of nuclear energy and beyond, E=mc² continues to shape our understanding of the cosmos and our place within it. This equation is not simply a formula; it's a window into the fundamental structure of reality.
Latest Posts
Latest Posts
-
1 6 Is Equal To
Sep 13, 2025
-
Gcf Of 12 And 40
Sep 13, 2025
-
Equivalent Fraction Of 3 6
Sep 13, 2025
-
0 25 Acres In Square Feet
Sep 13, 2025
-
6 5 As A Percentage
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Solve E Mc2 For C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.