Equivalent Fraction Of 3 6
saludintensiva
Sep 13, 2025 · 6 min read
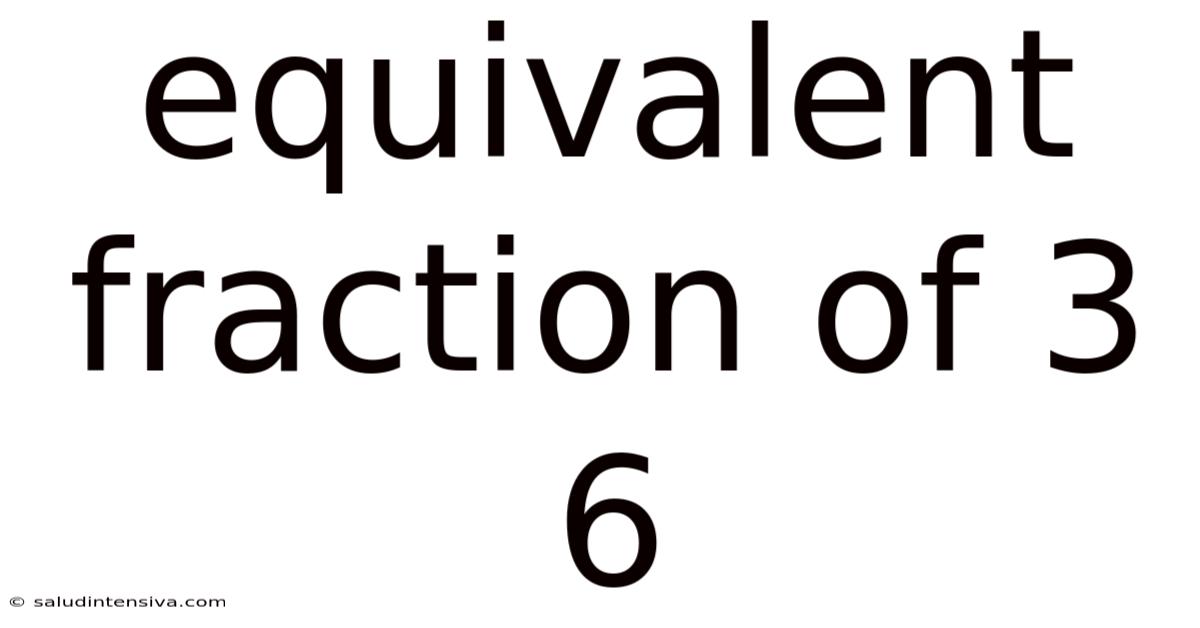
Table of Contents
Understanding Equivalent Fractions: A Deep Dive into 3/6
Equivalent fractions represent the same portion of a whole, even though they look different. Understanding equivalent fractions is fundamental to mastering fractions, decimals, and even more advanced mathematical concepts. This article will explore the concept of equivalent fractions, using 3/6 as our primary example, and delve into various methods for finding and verifying them. We'll also touch upon the practical applications and address frequently asked questions. By the end, you'll have a solid grasp of equivalent fractions and their significance in mathematics.
What are Equivalent Fractions?
Equivalent fractions are fractions that have different numerators and denominators but represent the same value or proportion. Think of it like this: cutting a pizza into six slices and taking three slices is the same as cutting a pizza into two slices and taking one. Both actions result in you consuming half of the pizza. This is the core idea behind equivalent fractions: they show the same part of a whole, just expressed differently. Our focus will be on understanding and finding equivalent fractions for 3/6.
Finding Equivalent Fractions for 3/6: Methods and Techniques
There are several ways to find equivalent fractions for 3/6. Let's explore the most common methods:
1. Multiplication (Scaling Up)
The simplest method is to multiply both the numerator and the denominator by the same number (other than zero). This essentially scales up the fraction, creating a larger but equivalent fraction.
For 3/6:
- Multiplying both by 2: (3 x 2) / (6 x 2) = 6/12
- Multiplying both by 3: (3 x 3) / (6 x 3) = 9/18
- Multiplying both by 4: (3 x 4) / (6 x 4) = 12/24
- And so on…
Each of these fractions – 6/12, 9/18, 12/24, etc. – is equivalent to 3/6. They all represent exactly one-half of a whole.
2. Division (Simplifying or Reducing)
The opposite of multiplication is division. We can simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For 3/6:
The GCD of 3 and 6 is 3. Dividing both by 3: (3 ÷ 3) / (6 ÷ 3) = 1/2
This shows that 3/6 simplifies to its simplest form, 1/2. This is the most reduced form of the equivalent fractions; it's the smallest whole number representation of that proportion.
3. Visual Representation
Visual aids can be incredibly helpful in understanding equivalent fractions. Imagine a rectangular bar divided into six equal parts. Shade three of them. This visually represents 3/6. Now, imagine dividing the same bar into twelve equal parts. Shading six of those parts will show the same area shaded as the 3/6 representation, visually demonstrating that 3/6 and 6/12 are equivalent. You can apply this to other equivalent fractions by altering the number of divisions.
The Significance of the Simplest Form (1/2)
The simplest form of a fraction, also known as the reduced fraction, is crucial for several reasons:
- Clarity: 1/2 is much easier to understand and work with than 3/6, 6/12, or any other equivalent fraction.
- Efficiency: Using the simplest form avoids unnecessary calculations and makes comparisons easier.
- Standardization: In many mathematical contexts, it's customary to present fractions in their simplest form for consistency and clarity.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions isn't just an abstract mathematical concept; it has numerous real-world applications:
- Cooking and Baking: Recipes often use fractions. Knowing equivalent fractions allows you to adjust recipes easily, such as doubling a recipe that calls for 3/6 of a cup of sugar to 6/12 of a cup.
- Measurement: Whether it's measuring lengths, weights, or volumes, equivalent fractions are essential for converting between different units.
- Data Analysis: Understanding proportions and percentages often relies on working with equivalent fractions. For instance, expressing 3/6 as 50% (which is equivalent to 1/2) allows for easier comparison and analysis of data.
- Construction and Engineering: Accurate measurements and proportions are paramount in construction and engineering, and equivalent fractions are frequently utilized for scaling blueprints and calculating material quantities.
- Financial Mathematics: Percentages, ratios, and proportions are heavily used in finance. A strong understanding of equivalent fractions underpins calculations related to interest rates, profits, losses, and more.
Beyond 3/6: Generalizing the Concept
The principles discussed for 3/6 apply to all fractions. To find equivalent fractions for any given fraction, simply multiply or divide both the numerator and the denominator by the same non-zero number. Remember that simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
Working with Equivalent Fractions: A Step-by-Step Example
Let's work through an example that incorporates the concepts we've discussed.
Problem: Determine if 15/20 and 3/4 are equivalent fractions.
Step 1: Simplify 15/20:
The GCD of 15 and 20 is 5. Dividing both by 5: (15 ÷ 5) / (20 ÷ 5) = 3/4
Step 2: Compare:
Now we see that 15/20 simplifies to 3/4. Since both fractions reduce to the same simplest form, they are equivalent.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to understand, compare, and work with in calculations. It also presents the fraction in its most concise and efficient form.
Q2: Can any fraction be expressed as an equivalent fraction?
A2: Yes, any fraction (except for fractions with a denominator of zero, which are undefined) can have infinitely many equivalent fractions created by multiplying the numerator and denominator by any non-zero number.
Q3: How do I find the greatest common divisor (GCD)?
A3: There are several methods to find the GCD, including listing factors, using prime factorization, and employing the Euclidean algorithm. Many calculators and online tools can also calculate the GCD.
Q4: What if I multiply or divide the numerator and denominator by different numbers?
A4: If you multiply or divide the numerator and denominator by different numbers, you will create a fraction that is not equivalent to the original fraction. Maintaining the same multiplier or divisor for both is crucial to generating equivalent fractions.
Q5: Are there any limits to finding equivalent fractions?
A5: Technically, there are infinitely many equivalent fractions for any given fraction because you can continually multiply the numerator and denominator by increasingly larger numbers. However, in practical applications, you'll typically work with fractions that are relatively easy to understand and use.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical literacy. By mastering the techniques of multiplication, division, and visualization, you can confidently navigate the world of fractions, simplifying them, comparing them, and applying them to diverse real-world scenarios. Remember that simplifying to the simplest form provides clarity and efficiency, and that the fundamental principle remains consistent across all fractions: multiplying or dividing both the numerator and denominator by the same non-zero number yields an equivalent fraction. With practice, you'll find that working with equivalent fractions becomes intuitive and second nature.
Latest Posts
Latest Posts
-
Lcm Of 3 And 15
Sep 13, 2025
-
Gram To Troy Oz Calculator
Sep 13, 2025
-
What Time Is 19 37
Sep 13, 2025
-
19 20 In Decimal Form
Sep 13, 2025
-
Gcf Of 10 And 30
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Equivalent Fraction Of 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.