6 16 In Simplest Form
saludintensiva
Sep 15, 2025 · 6 min read
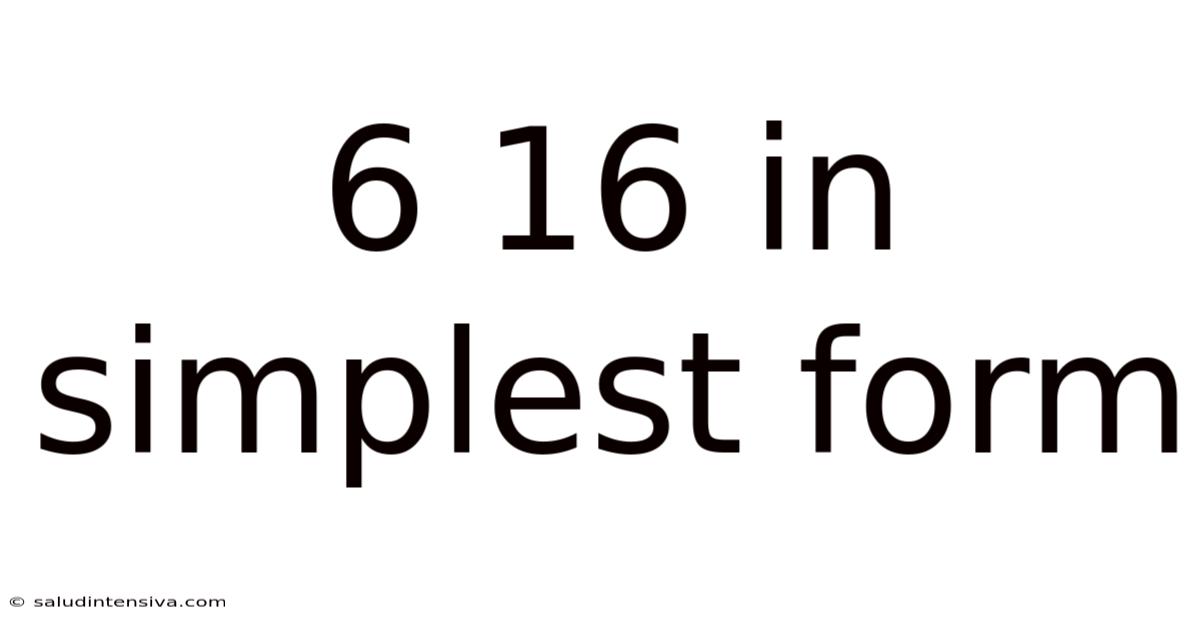
Table of Contents
Simplifying Fractions: A Deep Dive into 6/16
Understanding fractions is a fundamental concept in mathematics, essential for everything from baking a cake to understanding complex scientific formulas. This article will explore the simplification of fractions, using the example of 6/16, and delve into the underlying principles in a clear and accessible way. We’ll cover the steps involved, the mathematical reasoning behind them, and answer frequently asked questions. By the end, you'll not only know the simplest form of 6/16 but also possess a solid understanding of fraction simplification techniques applicable to any fraction.
Introduction: What are Fractions and Why Simplify Them?
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 6/16, 6 is the numerator and 16 is the denominator. This means we have 6 parts out of a total of 16 equal parts.
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means expressing the fraction using the smallest possible whole numbers for both the numerator and the denominator. While 6/16 is perfectly valid, it's not in its simplest form. Simplifying fractions makes them easier to understand, compare, and use in calculations. It's like cleaning up a messy room – the underlying value remains the same, but the organization is improved.
Step-by-Step Simplification of 6/16
To simplify 6/16, we need to find the greatest common divisor (GCD) of both the numerator (6) and the denominator (16). The GCD is the largest number that divides both 6 and 16 without leaving a remainder.
Here’s how we can find the GCD:
-
List the factors of each number:
- Factors of 6: 1, 2, 3, 6
- Factors of 16: 1, 2, 4, 8, 16
-
Identify the common factors: The common factors of 6 and 16 are 1 and 2.
-
Determine the greatest common factor: The largest of these common factors is 2. Therefore, the GCD of 6 and 16 is 2.
-
Divide both the numerator and the denominator by the GCD:
6 ÷ 2 = 3 16 ÷ 2 = 8
Therefore, the simplified form of 6/16 is 3/8.
Alternative Methods for Finding the GCD
While listing factors works well for smaller numbers, it becomes less efficient for larger numbers. Here are two alternative methods for finding the GCD:
-
Prime Factorization: This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 6: 2 x 3
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2<sup>4</sup>
The common prime factor is 2 (it appears once in the factorization of 6 and four times in the factorization of 16). The GCD is the product of the common prime factors raised to the lowest power, which is 2<sup>1</sup> = 2.
-
Euclidean Algorithm: This is a more sophisticated method, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide the larger number (16) by the smaller number (6): 16 ÷ 6 = 2 with a remainder of 4.
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (4): 6 ÷ 4 = 1 with a remainder of 2.
- Repeat: 4 ÷ 2 = 2 with a remainder of 0.
- The last non-zero remainder is 2, so the GCD is 2.
Visual Representation of Fraction Simplification
Imagine you have a pizza cut into 16 slices. You have 6 of those slices (6/16). If you group the slices into pairs, you'll have 3 groups of 2 slices out of a total of 8 groups of 2 slices. This visually represents the simplification from 6/16 to 3/8. The size of the pizza slices (the value of the fraction) doesn't change; only the way they are grouped changes.
The Importance of Simplifying Fractions in Real-World Applications
Simplifying fractions is crucial in various real-world applications:
-
Cooking and Baking: Recipes often use fractions. Simplifying fractions helps you easily understand and measure ingredients accurately.
-
Construction and Engineering: Precise measurements are essential in these fields. Simplifying fractions ensures accuracy in calculations and plans.
-
Finance: Dealing with percentages and proportions frequently involves fractions. Simplification improves clarity and efficiency in financial calculations.
-
Data Analysis: When working with data, simplifying fractions makes interpreting results easier and more intuitive.
Frequently Asked Questions (FAQs)
Q1: Can all fractions be simplified?
A1: No. Some fractions are already in their simplest form. For example, 1/2, 3/7, and 5/11 are already simplified because the numerator and denominator share no common factors other than 1.
Q2: What if I divide by a number that isn't the GCD?
A2: You'll still get a simplified fraction, but it won't be in the lowest terms. For example, if you divide 6/16 by 1, you still get 6/16. If you divide it by only one of its common factors (e.g., 1), it will still be equivalent to 6/16, which is not the simplest form. Dividing by a common factor that is less than the GCD requires more than one step to reach the simplest form.
Q3: How can I check if my simplified fraction is correct?
A3: You can check your answer by multiplying the simplified fraction by the GCD. For 3/8 (simplified from 6/16), multiplying by 2 (the GCD) gives (3 x 2) / (8 x 2) = 6/16, confirming that your simplification is correct.
Q4: What happens if the numerator is larger than the denominator?
A4: That’s an improper fraction. You can simplify an improper fraction the same way as a proper fraction (numerator smaller than denominator). After simplification, you can then convert it to a mixed number (a whole number and a fraction). For example, 16/8 simplifies to 2/1, or simply 2.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill with broad applications. While seemingly simple, understanding the underlying principles of GCD and different methods for finding it allows for efficient and accurate simplification of any fraction, regardless of its size. By mastering these techniques, you’ll not only improve your mathematical skills but also enhance your problem-solving abilities in various real-world situations. The journey from 6/16 to 3/8 is a small step, but it demonstrates a significant mathematical principle. Remember that practice is key; the more you work with fractions, the more comfortable and efficient you'll become.
Latest Posts
Latest Posts
-
Hcf Of 2 And 3
Sep 16, 2025
-
Sum And Difference Formulas Calculator
Sep 16, 2025
-
Equivalent Fractions For 1 2
Sep 16, 2025
-
Gcf Of 36 And 20
Sep 16, 2025
-
Rounding To Nearest Ten Thousand
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 6 16 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.