6 Divided By 1 4
saludintensiva
Sep 14, 2025 · 5 min read
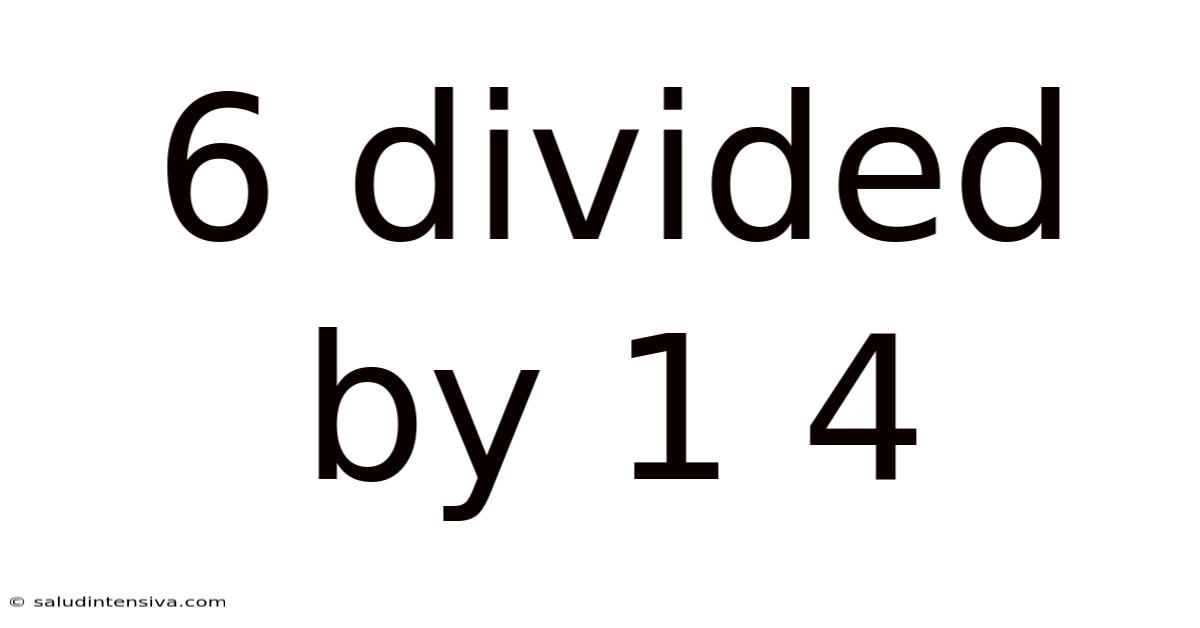
Table of Contents
6 Divided by 1/4: Unveiling the Math Behind the Mystery
Understanding division, especially when fractions are involved, can sometimes feel like navigating a mathematical maze. This comprehensive guide will unravel the mystery behind 6 divided by 1/4, providing a clear, step-by-step explanation suitable for learners of all levels. We'll explore the underlying principles, offer multiple approaches to solving the problem, and address common misconceptions. By the end, you'll not only know the answer but also possess a deeper understanding of fraction division.
Introduction: Deconstructing the Problem
The question "6 divided by 1/4" (often written as 6 ÷ 1/4 or 6 / (1/4)) might seem deceptively simple at first glance. However, it highlights a crucial concept in arithmetic: dividing by a fraction is the same as multiplying by its reciprocal. This seemingly small detail is the key to unlocking the solution and mastering this type of problem. We'll break down this concept and explore various methods to solve this specific problem and similar ones involving fraction division.
Method 1: The Reciprocal Approach
The most efficient method for dividing by a fraction is to convert the division problem into a multiplication problem. To do this, we use the reciprocal of the fraction we're dividing by. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/4 is 4/1 (or simply 4).
Therefore, the problem 6 ÷ 1/4 becomes 6 x 4. This is a much simpler multiplication problem, and the answer is straightforward: 6 x 4 = 24.
Method 2: Visual Representation with Models
Let's visualize the problem using a model. Imagine you have 6 whole pizzas. Dividing by 1/4 means finding out how many 1/4 slices are in those 6 pizzas.
Each pizza can be divided into four 1/4 slices. Since you have 6 pizzas, the total number of 1/4 slices is 6 pizzas x 4 slices/pizza = 24 slices. Therefore, 6 divided by 1/4 equals 24.
Method 3: Understanding Division as Repeated Subtraction
Division can also be understood as repeated subtraction. How many times can you subtract 1/4 from 6?
We can represent 6 as 24/4 (since 24/4 = 6). Now, we're asking how many times 1/4 goes into 24/4. This is equivalent to asking how many times 1 goes into 24, which is 24. This method highlights the underlying connection between division and repeated subtraction.
Method 4: Converting to Improper Fractions
Another approach involves converting the whole number into a fraction. We can rewrite 6 as 6/1. Now, our problem becomes (6/1) ÷ (1/4). Remember the rule for dividing fractions: keep the first fraction, change the division sign to multiplication, and flip (take the reciprocal of) the second fraction.
This gives us: (6/1) x (4/1) = 24/1 = 24. This method reinforces the importance of understanding fraction operations.
The Importance of Understanding Reciprocals
The concept of reciprocals is central to understanding fraction division. A reciprocal, also known as a multiplicative inverse, is a number that, when multiplied by the original number, results in 1. For example, the reciprocal of 2 is 1/2 (because 2 x 1/2 = 1), and the reciprocal of 1/4 is 4 (because 1/4 x 4 = 1).
Mastering reciprocals is crucial for solving problems involving fraction division efficiently and accurately. It allows you to convert a complex division problem into a simpler multiplication problem, which is often easier to solve.
Expanding the Concept: Generalizing Fraction Division
The method we used to solve 6 ÷ 1/4 can be generalized to solve any problem involving the division of a whole number by a fraction. The general rule is:
- a ÷ (b/c) = a x (c/b)
Where 'a' is the whole number, and 'b/c' is the fraction. We simply multiply the whole number by the reciprocal of the fraction.
Example: Let's solve 10 ÷ (2/5).
Following the rule, we have: 10 x (5/2) = 50/2 = 25
This general approach streamlines the process of solving fraction division problems.
Addressing Common Misconceptions
One common misconception is simply multiplying the whole number by the numerator and the denominator of the fraction. This is incorrect. Always remember to use the reciprocal of the fraction before multiplying.
Another misconception involves confusing division and multiplication with fractions. While closely related, they are distinct operations requiring different procedures.
Frequently Asked Questions (FAQs)
-
Q: Why do we use the reciprocal when dividing fractions?
A: Dividing by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental property of fraction arithmetic and simplifies the calculation process.
-
Q: What if I'm dividing a fraction by a whole number?
A: The principle remains the same. You still use the reciprocal, though in this case, you'd convert the whole number into a fraction (e.g., 5 becomes 5/1) and then proceed with the reciprocal method.
-
Q: Can I use a calculator to solve these problems?
A: Yes, calculators can be used, but understanding the underlying principles is crucial for solving more complex problems and building a strong mathematical foundation.
Conclusion: Mastering Fraction Division
Understanding the division of whole numbers by fractions is a vital skill in mathematics. By grasping the concept of reciprocals and applying the techniques outlined in this article, you can confidently tackle similar problems. Remember to practice regularly to reinforce your understanding and build your mathematical fluency. The ability to solve fraction division problems efficiently and accurately opens doors to more advanced mathematical concepts. Through practice and a clear understanding of the underlying principles, this seemingly complex mathematical operation can be easily mastered. The journey towards mathematical proficiency is often built upon these foundational concepts.
Latest Posts
Latest Posts
-
9 To The 6 Power
Sep 14, 2025
-
17 25 As A Percent
Sep 14, 2025
-
40 Percent As A Fraction
Sep 14, 2025
-
1 Meter 64 In Feet
Sep 14, 2025
-
2 3 8 In Decimal
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.