7 15 As A Percent
saludintensiva
Sep 23, 2025 · 5 min read
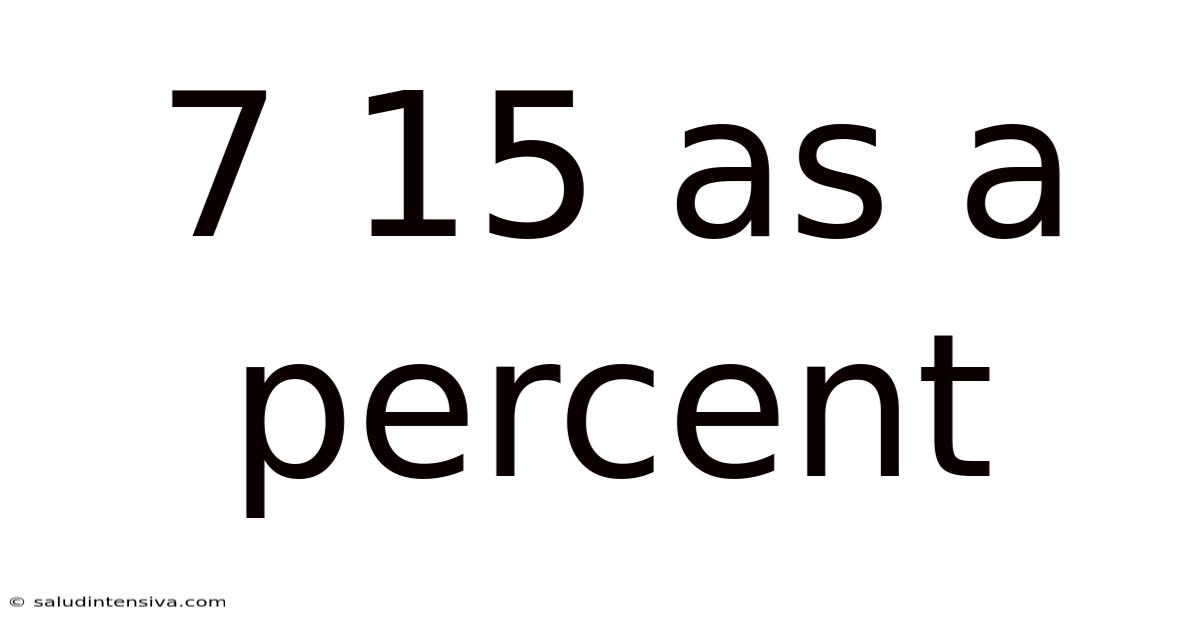
Table of Contents
7/15 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will delve into the process of converting the fraction 7/15 into a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also explore different methods, tackling potential difficulties and offering insightful tips along the way. This will cover not just the answer but the why behind the calculations, empowering you to confidently tackle similar conversions in the future.
Understanding Fractions and Percentages
Before we embark on the conversion of 7/15, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 7/15, 7 is the numerator and 15 is the denominator. This means we're considering 7 parts out of a total of 15 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 constitute a given portion. For example, 50% means 50 parts out of 100, which is equivalent to the fraction 50/100, or 1/2.
Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100, or, more generally, expressing the fraction as a decimal and then multiplying by 100.
Method 1: Direct Conversion using Division
The most straightforward method to convert 7/15 to a percentage is through division.
-
Divide the numerator by the denominator: Divide 7 by 15. This gives you a decimal value. 7 ÷ 15 ≈ 0.466666...
-
Multiply the decimal by 100: To convert the decimal to a percentage, multiply the result by 100. 0.466666... × 100 ≈ 46.6666...%
-
Round to the desired precision: Since the decimal is repeating, you'll likely want to round the percentage to a certain number of decimal places. Rounding to two decimal places gives us 46.67%.
Therefore, 7/15 is approximately 46.67%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
While the division method is efficient, understanding the concept of equivalent fractions can be equally valuable. The aim is to find a fraction equivalent to 7/15 but with a denominator of 100.
This involves finding a number that, when multiplied by 15, results in 100. Unfortunately, there is no whole number that satisfies this condition. 100 is not a multiple of 15. This highlights why the division method is often more practical for fractions that don't readily simplify to a denominator of 100. However, we can still utilize this approach to illustrate the underlying principle.
Instead of aiming for a denominator of 100 directly, we can find an equivalent decimal and then convert that to a percentage. Dividing 7 by 15 (as shown in Method 1) gives us approximately 0.4667. Multiplying this decimal by 100/100 (which is essentially multiplying by 1 and doesn't change the value) gives us:
0.4667 * 100/100 = (0.4667 * 100)/100 ≈ 46.67/100 = 46.67%
Method 3: Using Proportions
Another way to approach this problem is through setting up a proportion. We can represent the fraction 7/15 as a proportion to find the equivalent percentage:
7/15 = x/100
Where 'x' represents the percentage we're trying to find.
To solve for 'x', we cross-multiply:
15x = 700
Then, divide both sides by 15:
x = 700/15 ≈ 46.67
Therefore, x ≈ 46.67%, which confirms our previous results.
Understanding the Decimal Approximation
It's important to acknowledge that the result, 46.67%, is an approximation. The decimal representation of 7/15 is a repeating decimal (0.46666...). Rounding is necessary to represent it in a practical and manageable format. The level of precision (number of decimal places) depends on the context of the problem. For most applications, rounding to two decimal places (46.67%) is sufficient.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
-
Calculating Grades: If you scored 7 out of 15 on a quiz, your percentage score would be approximately 46.67%.
-
Financial Calculations: Understanding percentages is essential for calculating interest rates, discounts, and profit margins.
-
Data Analysis: In statistical analysis, data is often presented as percentages to facilitate comparison and interpretation.
-
Recipe Scaling: Adjusting ingredient quantities in recipes frequently involves converting fractions to percentages.
-
Probability and Statistics: Determining probabilities often involves converting fractions representing the likelihood of an event into percentages.
Frequently Asked Questions (FAQ)
Q: Why is 7/15 not easily converted to a percentage with a whole number?
A: Because 15 does not divide evenly into 100. To convert a fraction to a percentage directly without division, the denominator must be a factor of 100 (1, 2, 4, 5, 10, 20, 25, 50, 100).
Q: What if I need a more precise percentage than 46.67%?
A: You can use more decimal places in your calculation and rounding. However, for most practical purposes, two decimal places offer sufficient accuracy.
Q: Are there other ways to convert fractions to percentages?
A: Yes, you can use calculators or software specifically designed for mathematical conversions. Many spreadsheet programs (like Excel or Google Sheets) readily handle fraction-to-percentage conversions.
Q: What happens if the numerator is larger than the denominator?
A: If the numerator is larger than the denominator (e.g., 17/15), the resulting percentage will be greater than 100%. This indicates a value exceeding the whole.
Conclusion
Converting 7/15 to a percentage involves a straightforward process, primarily relying on division and multiplication. While the precise value is a repeating decimal, rounding to 46.67% provides a practical and sufficiently accurate approximation for most purposes. Understanding the underlying principles of fractions and percentages, along with the various methods of conversion, empowers you to tackle similar problems with confidence and apply this fundamental skill in various mathematical and real-world contexts. Remember to choose the method most comfortable and efficient for you, but always strive for understanding the fundamental concepts involved.
Latest Posts
Latest Posts
-
4 2 3 As Decimal
Sep 23, 2025
-
48 Inches Tall In Feet
Sep 23, 2025
-
How Many Gallons Gas Tank
Sep 23, 2025
-
36 Feet How Many Yards
Sep 23, 2025
-
11 7 As A Mixed Number
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 7 15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.