7 4 As A Decimal
saludintensiva
Sep 16, 2025 · 6 min read
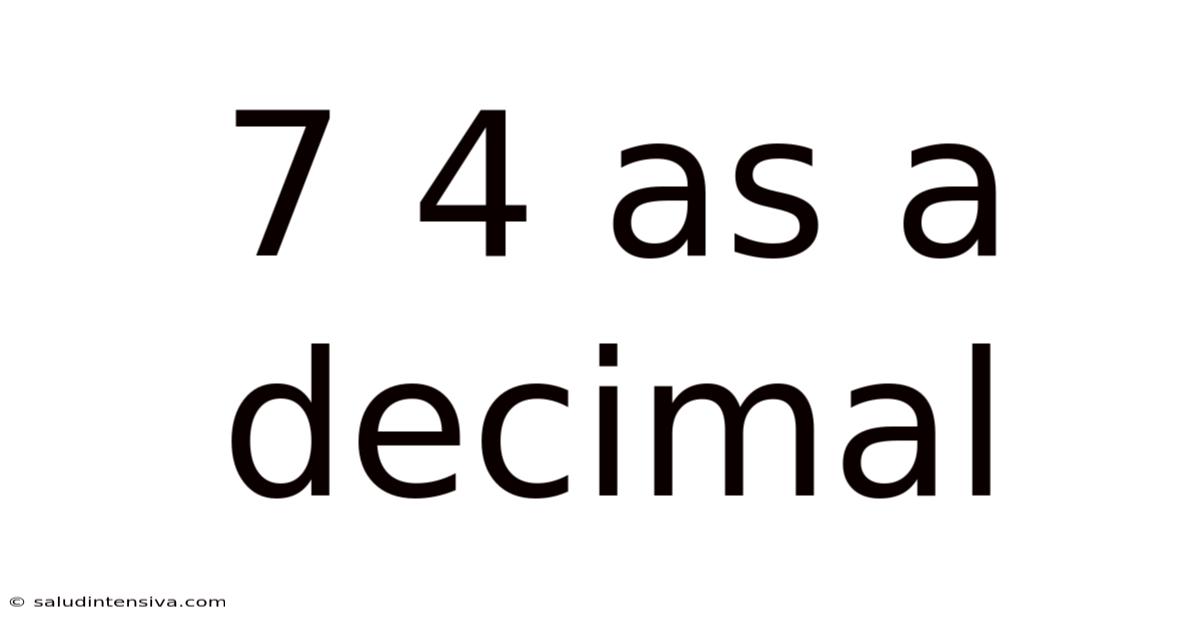
Table of Contents
7/4 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the conversion of the fraction 7/4 to its decimal equivalent, exploring different methods, underlying principles, and practical applications. Understanding this simple conversion can unlock a deeper understanding of number systems and their interrelationships.
Introduction: Understanding Fractions and Decimals
Before we dive into the conversion of 7/4, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a number using the base-10 system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
The fraction 7/4 signifies seven parts out of four equal parts. This immediately tells us that the decimal representation will be greater than 1, since 7 is larger than 4. We'll explore several methods to achieve this conversion accurately.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (4).
- Set up the division: Write 7 as the dividend and 4 as the divisor.
- Divide: 4 goes into 7 one time (4 x 1 = 4). Subtract 4 from 7, leaving a remainder of 3.
- Add a decimal point and a zero: Add a decimal point to the quotient (the result of the division) and a zero to the remainder (3). This allows us to continue the division process.
- Continue dividing: 4 goes into 30 seven times (4 x 7 = 28). Subtract 28 from 30, leaving a remainder of 2.
- Repeat: Add another zero to the remainder. 4 goes into 20 five times (4 x 5 = 20). The remainder is 0.
- Final Result: The complete division yields 1.75.
Therefore, 7/4 as a decimal is 1.75.
Method 2: Equivalent Fractions
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). While not always possible directly, it can be a useful technique in certain cases.
In this instance, we can't easily find a whole number to multiply both the numerator and denominator of 7/4 to get a power of 10 as the denominator. Therefore, long division remains the more practical method for this specific fraction. However, understanding this method helps with fractions that can be easily converted to a denominator that is a power of 10. For example, converting 1/2 to a decimal is easily done by multiplying both numerator and denominator by 5 to obtain 5/10, which is 0.5.
Method 3: Using a Calculator
Modern calculators provide a simple and quick way to convert fractions to decimals. Simply enter the fraction as 7 ÷ 4, and the calculator will directly provide the decimal equivalent: 1.75. While convenient, it's crucial to understand the underlying mathematical principles behind the conversion, as calculators don't always reveal the how behind the what.
Understanding the Result: 1.75
The decimal representation 1.75 signifies one whole unit and seventy-five hundredths of a unit. Visually, you can imagine this as one whole object and 75/100 of another. This is equivalent to one and three-quarters (1 ¾).
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is invaluable in numerous applications:
- Everyday calculations: Sharing costs equally among friends, calculating discounts, or determining the total price including sales tax often involves fractional and decimal representations.
- Finance: Calculating interest, determining loan payments, and understanding financial statements heavily rely on decimal computations.
- Science and engineering: Measurements, data analysis, and scientific computations frequently use decimals for precision and ease of manipulation.
- Computer programming: Many programming languages use floating-point numbers (decimal representation) for numerical computations.
- Data analysis and statistics: Decimals are essential for representing statistical measures such as means, medians, and standard deviations.
Further Exploration: Converting Improper Fractions and Mixed Numbers
The fraction 7/4 is an improper fraction because the numerator (7) is larger than the denominator (4). This is contrasted with a proper fraction, where the numerator is smaller than the denominator (e.g., 3/4).
Improper fractions can also be expressed as mixed numbers. A mixed number combines a whole number and a proper fraction. In the case of 7/4, the equivalent mixed number is 1 ¾. The conversion process is straightforward: divide the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the proper fraction, retaining the original denominator.
The conversion between improper fractions, mixed numbers, and decimals provides flexibility in representing numerical values and choosing the most convenient form for specific contexts.
Frequently Asked Questions (FAQ)
Q: Why is it important to understand fraction-to-decimal conversion?
A: It's fundamental for mathematical literacy and essential for various applications in everyday life, finance, science, and technology. The ability to switch between fractional and decimal representations enhances problem-solving abilities and provides a deeper understanding of number systems.
Q: Are there any other methods to convert 7/4 to a decimal besides long division?
A: While long division is the most direct method for this specific fraction, using a calculator offers a quicker approach. The method of equivalent fractions is also a viable technique, though not always easily applicable.
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that have prime factors other than 2 and 5 will result in non-terminating, repeating decimals. For example, 1/3 converts to 0.333... (a repeating decimal).
Q: What if I have a more complex fraction?
A: The same principles apply to more complex fractions. Long division remains a reliable method, although the process may become more lengthy. Calculators can handle more complex calculations efficiently.
Q: How can I improve my skills in fraction-to-decimal conversion?
A: Practice is key. Start with simple fractions, gradually increasing the complexity. Understanding the underlying mathematical principles is crucial for tackling more challenging conversions confidently. Utilize various methods (long division, equivalent fractions, calculators) to reinforce your understanding.
Conclusion: Mastering Decimal Conversion
Converting fractions to decimals is a crucial skill that extends far beyond the realm of basic arithmetic. This guide has explored the various methods for converting the fraction 7/4 to its decimal equivalent (1.75), highlighting the importance of understanding both the process and the underlying mathematical concepts. Mastering this skill empowers you to approach various mathematical and real-world problems with increased confidence and efficiency. By understanding the different methods and their applications, you'll be well-equipped to handle a wide range of numerical conversions. The ability to seamlessly transition between fractions and decimals is a cornerstone of mathematical proficiency, opening doors to more advanced concepts and problem-solving opportunities.
Latest Posts
Latest Posts
-
1 2 As A Mixed Number
Sep 16, 2025
-
Lcm Of 22 And 33
Sep 16, 2025
-
2 3 Acres To Square Feet
Sep 16, 2025
-
How Long Is 16 Hours
Sep 16, 2025
-
4 1 8 Improper Fraction
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 7 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.