1/2 As A Mixed Number
saludintensiva
Sep 16, 2025 · 6 min read
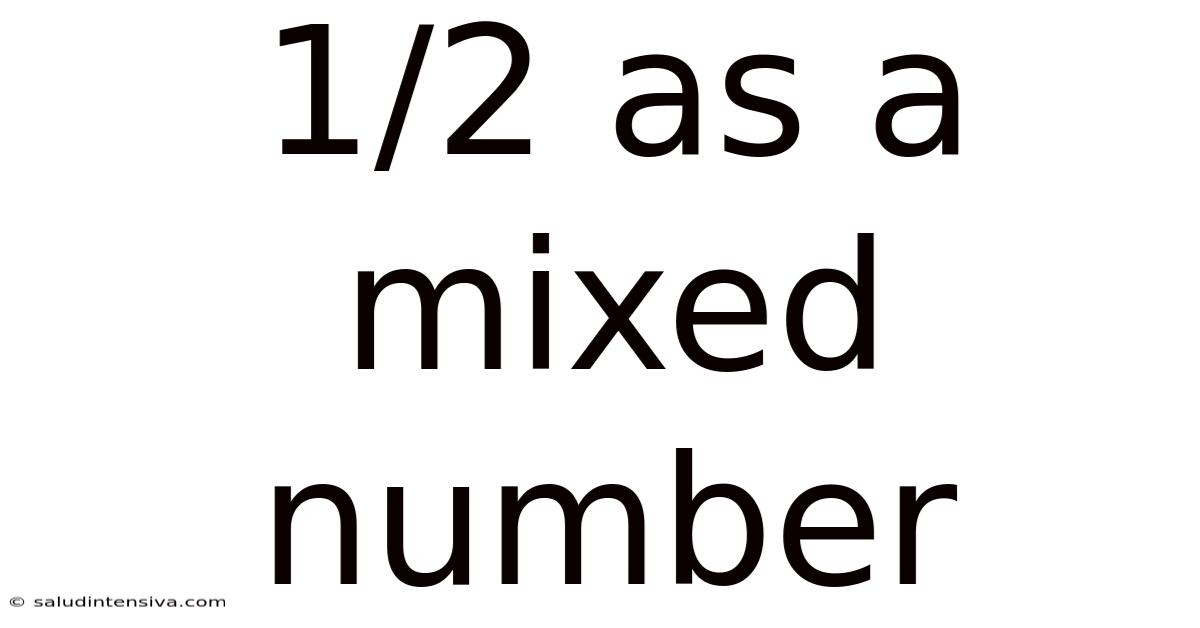
Table of Contents
Understanding 1/2 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 1/2 often presents a minor hurdle for those new to working with mixed numbers. While 1/2 is already in its simplest form as a fraction, understanding its representation as a mixed number – and the broader concepts involved – is crucial for mastering more complex fraction manipulation. This comprehensive guide will delve into the meaning of mixed numbers, explore how 1/2 relates to them, and provide a solid foundation for future mathematical endeavors. We'll cover the conversion process, delve into the underlying mathematical principles, and address common questions and misconceptions.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number), indicating a value less than one. For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that's greater than one. Understanding mixed numbers is vital in various real-world applications, from cooking and measuring to advanced mathematical calculations.
Why Can't 1/2 Be Expressed as a Mixed Number?
This is where we get to the heart of the matter. The key to understanding why 1/2 can't be expressed as a mixed number lies in the definition itself. A mixed number must have a whole number component greater than zero and a proper fraction component. 1/2, on its own, represents a value less than one. There's no whole number part to include. Trying to force a whole number component would result in an improper fraction (where the numerator is greater than or equal to the denominator), which is a different representation entirely.
Let's illustrate this with an example using a fraction that can be expressed as a mixed number: 7/4.
We can divide the numerator (7) by the denominator (4): 7 ÷ 4 = 1 with a remainder of 3. This gives us our mixed number: 1 ¾. The quotient (1) becomes the whole number, and the remainder (3) becomes the numerator of the fraction, keeping the original denominator (4).
However, with 1/2, the division yields: 1 ÷ 2 = 0 with a remainder of 1. There is no whole number component, only the proper fraction 1/2. Therefore, there isn't a valid mixed number representation.
Improper Fractions vs. Mixed Numbers: A Crucial Distinction
To fully grasp the concept, we need to understand the difference between improper fractions and mixed numbers.
-
Improper Fraction: An improper fraction has a numerator greater than or equal to its denominator. Examples include 7/4, 5/5, and 11/3. These fractions represent a value greater than or equal to one.
-
Mixed Number: A mixed number, as previously discussed, combines a whole number and a proper fraction. It also represents a value greater than one.
The relationship between them is that any improper fraction can be converted into a mixed number, and vice-versa. However, a proper fraction, like 1/2, cannot be directly converted into a mixed number because it already represents a value less than one.
Converting Improper Fractions to Mixed Numbers (and vice-versa)
Let's solidify the conversion process with a few examples, focusing on the crucial difference between fractions that can and cannot be expressed as mixed numbers.
Example 1 (Convertible): Convert the improper fraction 11/3 to a mixed number.
- Divide the numerator (11) by the denominator (3): 11 ÷ 3 = 3 with a remainder of 2.
- The quotient (3) becomes the whole number part of the mixed number.
- The remainder (2) becomes the numerator of the fraction, retaining the original denominator (3).
- Therefore, 11/3 as a mixed number is 3 ⅔.
Example 2 (Not Convertible): Attempting to convert 1/2 to a mixed number.
- Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0 with a remainder of 1.
- The quotient is 0, meaning there's no whole number part.
- The remainder (1) and the denominator (2) form the proper fraction 1/2.
- The result is simply 1/2 – it cannot be expressed as a mixed number.
Example 3 (Convertible): Convert the mixed number 2 ¾ to an improper fraction.
- Multiply the whole number (2) by the denominator (4): 2 x 4 = 8.
- Add the result (8) to the numerator (3): 8 + 3 = 11.
- Keep the original denominator (4).
- Therefore, 2 ¾ as an improper fraction is 11/4.
Practical Applications and Real-World Scenarios
Mixed numbers frequently appear in daily life, often related to measurements and quantities. Imagine baking a cake; a recipe might call for 2 ½ cups of flour. Here, the mixed number clearly conveys the amount needed, which would be less intuitive if represented solely as an improper fraction (5/2).
Similarly, measuring lengths – say, 3 ⅛ inches – naturally uses mixed numbers. These examples highlight the practical advantage of mixed numbers in representing quantities greater than one in a readily understandable manner. While improper fractions are mathematically equivalent, mixed numbers offer superior clarity and ease of interpretation in everyday situations.
Common Mistakes and Misconceptions
One common misconception is that any fraction can be converted into a mixed number. As demonstrated, this is incorrect. Only improper fractions can be transformed into mixed numbers. Proper fractions, like 1/2, 3/7, and 1/10, inherently represent values less than one and thus lack a whole number component.
Another mistake is confusing the process of converting between improper fractions and mixed numbers. Remember the steps: for converting an improper fraction, divide, then construct the mixed number using the quotient and remainder. For the reverse conversion, multiply, add, and retain the denominator.
Frequently Asked Questions (FAQ)
Q: Is there any situation where 1/2 could be considered in a way similar to a mixed number?
A: While 1/2 cannot be expressed as a mixed number, you might encounter scenarios where the concept is extended to include mixed fractions with zero as a whole number. For example, in advanced mathematical notations or programming, it might be represented as 0 1/2 for consistency or to simplify certain operations. However, this isn't standard practice in elementary or general mathematical contexts.
Q: Why is understanding mixed numbers important?
A: Mixed numbers are essential for understanding and working with fractions in real-world scenarios and more advanced mathematical concepts. They provide a more intuitive way to represent quantities greater than one, making calculations and interpretations easier in everyday situations.
Q: Are there any alternative ways to represent a value between 0 and 1?
A: Yes, besides proper fractions, decimals are another common representation. 1/2 is equivalent to 0.5. Decimals provide an alternative format for representing fractions, particularly useful in certain calculations and applications.
Conclusion
While 1/2 cannot be expressed as a mixed number due to the fundamental definition of a mixed number – requiring a whole number component greater than zero and a proper fraction – understanding this limitation clarifies the crucial distinction between proper fractions and improper fractions. This understanding, coupled with the knowledge of how to convert between improper fractions and mixed numbers, provides a strong foundation for confidently navigating fraction-based calculations and real-world applications. Remember that mixed numbers are a powerful tool, but their use is specifically tailored to representing values greater than one. Mastering the concepts outlined here will significantly enhance your mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
8 2 3 As A Decimal
Sep 16, 2025
-
1 1 4 Simplest Form
Sep 16, 2025
-
Gcf Of 15 And 36
Sep 16, 2025
-
6 1 2 As A Decimal
Sep 16, 2025
-
Spanish Numbers To Words Converter
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/2 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.