8 2 As A Decimal
saludintensiva
Sep 23, 2025 · 7 min read
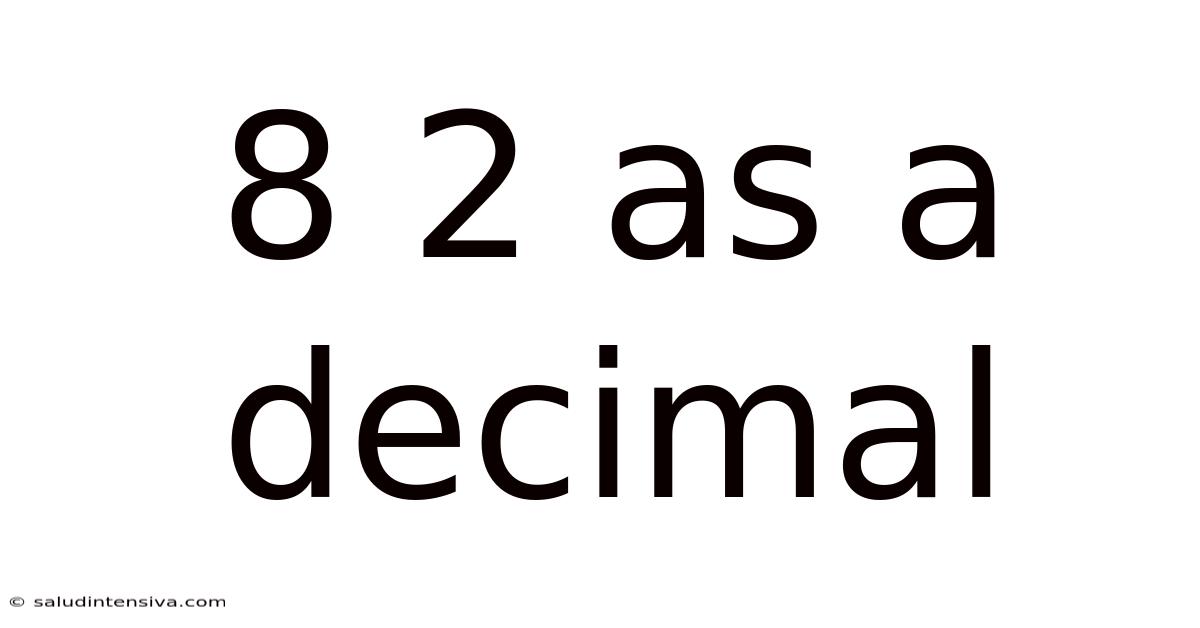
Table of Contents
Understanding 8/2 as a Decimal: A Comprehensive Guide
The seemingly simple fraction 8/2 often serves as a foundational stepping stone in understanding decimals and their relationship to fractions. While the answer might appear instantly obvious to some, exploring this seemingly basic conversion offers a valuable opportunity to solidify fundamental mathematical concepts and explore different approaches to problem-solving. This comprehensive guide will delve into various methods of converting 8/2 to its decimal equivalent, examining the underlying principles and addressing frequently asked questions. This will provide a solid understanding not just of this specific conversion, but also the broader concepts of fractions, decimals, and division.
Understanding Fractions and Decimals
Before diving into the conversion of 8/2, let's briefly review the core concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 8/2, 8 is the numerator and 2 is the denominator. This means we have 8 parts out of a total of 2 parts.
A decimal, on the other hand, represents a number using a base-ten system, where the digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, and so on). For example, 0.5 represents five tenths (5/10), and 0.25 represents twenty-five hundredths (25/100).
Converting 8/2 to a Decimal: The Direct Approach
The most straightforward method to convert 8/2 to a decimal is through simple division. A fraction essentially represents a division problem. The numerator is divided by the denominator. In this case:
8 ÷ 2 = 4
Therefore, the decimal equivalent of 8/2 is 4.0. The ".0" emphasizes that this is a whole number, with no fractional part.
Visualizing the Conversion
Imagine you have 8 identical objects, and you want to divide them into 2 equal groups. How many objects would be in each group? The answer, of course, is 4. This visual representation directly mirrors the mathematical operation of 8 ÷ 2 = 4. This simple example highlights the intuitive relationship between fractions, division, and their decimal representations.
Exploring Equivalent Fractions
Before performing the division, it's helpful to understand the concept of equivalent fractions. Equivalent fractions represent the same value even though they look different. For example, 8/2 is equivalent to 4/1, 16/4, 24/6, and countless other fractions. Simplifying the fraction before conversion often makes the division process easier. In this specific case, 8/2 simplifies directly to 4/1, which clearly equals 4. This simplification process is crucial in handling more complex fractions.
Understanding the Role of the Denominator
The denominator of a fraction plays a significant role in determining the decimal representation. When the denominator is a power of 10 (10, 100, 1000, etc.), the conversion to a decimal is straightforward. For example, 3/10 = 0.3, and 25/100 = 0.25. However, when the denominator is not a power of 10, as in the case of fractions like 1/3 or 5/7, the decimal representation will be a repeating or non-terminating decimal. The simplicity of 8/2, with its denominator of 2 (a factor of 10), leads to a clean, whole number decimal representation.
Decimal Representation and Place Value
The decimal system is based on place value. Each digit's position relative to the decimal point determines its value. The digit immediately to the right of the decimal point represents tenths, the next digit represents hundredths, and so on. In the case of 4.0, the "4" is in the ones place, and the "0" is in the tenths place, clearly indicating the value is 4.
Extending the Concept to More Complex Fractions
While 8/2 provides a simple illustration, the principles discussed here apply to more complex fractions as well. Let's consider the fraction 17/5. To convert it to a decimal, we perform the division:
17 ÷ 5 = 3.4
Here, the decimal representation is 3.4, which means 3 and 4 tenths. The process remains the same: divide the numerator by the denominator. The key is understanding the division process and the meaning of the decimal places.
Long Division and Decimal Conversions
For fractions where the division doesn't result in a whole number, long division is necessary to obtain the decimal representation. Long division is a systematic method of dividing numbers, particularly useful for fractions that don't simplify easily or have large numerators and denominators. This methodical approach ensures accuracy and helps understand the process of generating the decimal representation beyond simple whole number conversions. Let's illustrate with an example: Converting 7/8 to a decimal using long division.
Steps:
- Set up the long division problem: 7 divided by 8.
- Since 8 doesn't go into 7, add a decimal point and a zero to the dividend (7.0).
- Now, 8 goes into 70 eight times (8 x 8 = 64). Write 8 above the decimal point.
- Subtract 64 from 70, leaving a remainder of 6.
- Add another zero to the remainder, making it 60.
- 8 goes into 60 seven times (8 x 7 = 56). Write 7 after the decimal point in the quotient.
- Subtract 56 from 60, leaving a remainder of 4.
- Continue adding zeros and repeating the process until you reach a desired level of accuracy or the remainder becomes zero (which happens in this case after some iterations).
This process yields the decimal representation of 7/8 as 0.875. This example demonstrates that even for fractions that don't immediately simplify to a whole number, a systematic approach like long division provides a clear path to finding the decimal equivalent.
Repeating Decimals
It's important to note that not all fractions produce terminating decimals. Some fractions result in repeating decimals, where one or more digits repeat infinitely. For example, 1/3 = 0.3333... (the 3 repeats indefinitely). This is denoted by placing a bar over the repeating digits (0.3̅). Understanding the concept of repeating decimals is crucial for a complete understanding of the relationship between fractions and decimals.
Frequently Asked Questions (FAQ)
Q1: Why is 8/2 a whole number, while other fractions might have decimal parts?
A1: Because 8 is perfectly divisible by 2, resulting in a whole number quotient. Other fractions might not have a numerator perfectly divisible by the denominator, leading to a remainder and thus a decimal part.
Q2: Can any fraction be converted to a decimal?
A2: Yes, every fraction can be converted to a decimal by dividing the numerator by the denominator. The resulting decimal may be terminating (ending) or repeating (non-terminating).
Q3: What if the denominator is zero?
A3: Division by zero is undefined in mathematics. A fraction with a denominator of zero is not a valid mathematical expression.
Q4: Are there alternative methods to convert fractions to decimals besides division?
A4: While division is the most direct method, other approaches involve manipulating the fraction to have a denominator that is a power of 10 (e.g., multiplying the numerator and denominator by a suitable factor), which makes the decimal conversion more readily apparent.
Conclusion
Converting 8/2 to a decimal, while seemingly trivial, provides a robust foundation for understanding the crucial connection between fractions and decimals. Through the exploration of various methods, including simple division, visualization, equivalent fractions, and even a brief look at long division and repeating decimals, we've gained a deeper appreciation for the fundamental concepts of arithmetic. This knowledge transcends the simple conversion of 8/2 and equips you to tackle more complex fraction-to-decimal conversions with confidence and a thorough understanding of the underlying mathematical principles. Remember, even simple mathematical problems can provide valuable insights into the broader landscape of mathematics, fostering a deeper appreciation and more robust problem-solving skills.
Latest Posts
Latest Posts
-
1 Yard Of Mulch Weight
Sep 23, 2025
-
How Thick Concrete For Sidewalk
Sep 23, 2025
-
10 Divided By 5 6
Sep 23, 2025
-
90 Days From August 26
Sep 23, 2025
-
Energy Stored Due To Elevation
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8 2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.