8 3/8 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
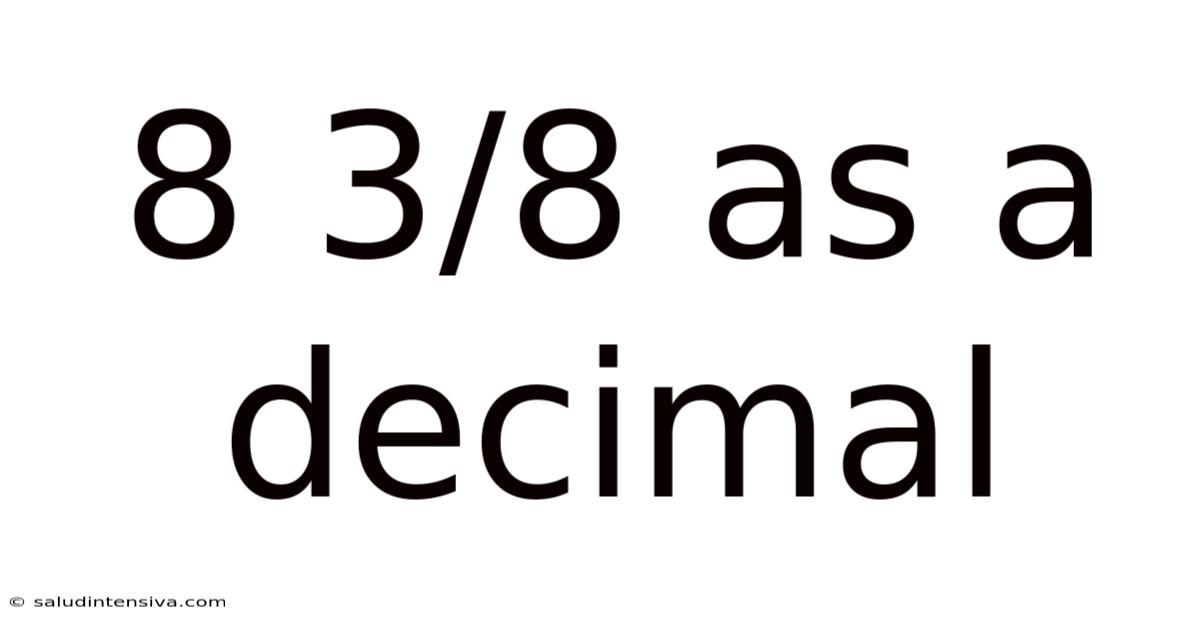
Table of Contents
8 3/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will walk you through the process of converting the mixed number 8 3/8 into its decimal equivalent, explaining the underlying principles and providing helpful tips for similar conversions. Understanding this process is key to mastering fraction-to-decimal conversions and building a strong foundation in arithmetic.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 8 3/8. This represents 8 whole units plus 3/8 of another unit. A decimal, on the other hand, uses a base-10 system to represent numbers, with a decimal point separating the whole number part from the fractional part. For example, 8.375 is a decimal number.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This method breaks down the conversion into two simpler steps. First, we convert the fractional part (3/8) into a decimal, and then we add the whole number (8).
Step 1: Converting the Fraction 3/8 to a Decimal
To convert a fraction to a decimal, we perform division. We divide the numerator (the top number) by the denominator (the bottom number):
3 ÷ 8 = 0.375
Step 2: Adding the Whole Number
Now, we simply add the whole number part (8) to the decimal equivalent of the fraction (0.375):
8 + 0.375 = 8.375
Therefore, 8 3/8 as a decimal is 8.375.
Method 2: Converting the Entire Mixed Number Directly
This method involves converting the entire mixed number into an improper fraction first, and then converting the improper fraction to a decimal.
Step 1: Converting the Mixed Number to an Improper Fraction
To convert a mixed number to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator of the fraction: 8 x 8 = 64
- Add the numerator of the fraction to the result: 64 + 3 = 67
- Keep the same denominator: 8
This gives us the improper fraction 67/8.
Step 2: Converting the Improper Fraction to a Decimal
Now, we divide the numerator (67) by the denominator (8):
67 ÷ 8 = 8.375
Again, we arrive at the decimal equivalent of 8.375.
Understanding the Decimal Representation: Place Value
The decimal 8.375 can be understood in terms of place value:
- 8: Represents 8 ones.
- 3: Represents 3 tenths (3/10).
- 7: Represents 7 hundredths (7/100).
- 5: Represents 5 thousandths (5/1000).
This means 8.375 is equal to 8 + 3/10 + 7/100 + 5/1000.
Why is Understanding Decimal Conversion Important?
The ability to convert fractions to decimals is essential for numerous reasons:
-
Everyday Calculations: Many everyday tasks, such as calculating discounts, splitting bills, or measuring ingredients, involve working with both fractions and decimals. Being able to seamlessly convert between the two simplifies these calculations.
-
Financial Literacy: Understanding decimals is critical for managing personal finances. Interest rates, loan payments, and stock prices are often expressed as decimals.
-
Scientific and Engineering Applications: In fields like science and engineering, precise measurements and calculations are paramount. Decimals provide a more accurate and convenient way to represent fractions in these contexts.
-
Computer Programming: Computers work with binary numbers, but many programming languages require working with decimal representations of numbers. Understanding decimal conversion is essential for programmers to accurately translate data and perform calculations.
-
Data Analysis: In data analysis and statistics, data is often represented using decimals. Converting fractions to decimals allows for easier manipulation and analysis of the data.
-
Advanced Mathematics: A strong grasp of decimal representation lays the foundation for more advanced mathematical concepts, including algebra, calculus, and trigonometry.
Practicing Fraction to Decimal Conversions
Mastering fraction-to-decimal conversions requires practice. Here are some examples to try:
- 5 1/2
- 2 3/4
- 1 7/8
- 10 1/5
- 9 2/3 (This will result in a repeating decimal)
Remember, the key is to understand the underlying principle of division. Once you grasp this, converting fractions to decimals becomes a straightforward process.
Frequently Asked Questions (FAQ)
Q: What if the fraction results in a repeating decimal?
A: Some fractions, like 1/3 (which equals 0.3333...), produce repeating decimals. In such cases, you can either express the decimal with a repeating bar notation (0.3̅) or round the decimal to a specific number of decimal places, depending on the level of precision required.
Q: Can I use a calculator to convert fractions to decimals?
A: Yes, most calculators have the functionality to perform division, which is the core of the fraction-to-decimal conversion process. Simply enter the numerator, then the division symbol, and then the denominator.
Q: Are there other ways to convert mixed numbers to decimals?
A: While the methods described above are the most common and straightforward, there are other approaches involving using equivalent fractions with denominators that are powers of 10 (e.g., 10, 100, 1000). However, these methods can be less efficient than the division method for most mixed numbers.
Conclusion
Converting 8 3/8 to a decimal, resulting in 8.375, demonstrates a crucial mathematical skill applicable in diverse contexts. By understanding the underlying principles of fraction-to-decimal conversion and practicing different methods, you can build a strong foundation in arithmetic and confidently tackle similar conversions in the future. The ability to seamlessly transition between fractions and decimals is not just a mathematical skill; it's a valuable tool for navigating various aspects of life, from personal finances to professional pursuits. Remember to practice regularly and don't hesitate to utilize calculators for complex calculations. With continued practice, this seemingly simple conversion will become second nature.
Latest Posts
Latest Posts
-
Gcf Of 36 And 45
Sep 10, 2025
-
Equivalent Fractions Of 2 5
Sep 10, 2025
-
109 Degrees Fahrenheit In Celsius
Sep 10, 2025
-
Lcm Of 20 And 24
Sep 10, 2025
-
What Is 2 3 2 3
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 8 3/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.