9 10 X 9 10
saludintensiva
Sep 10, 2025 · 6 min read
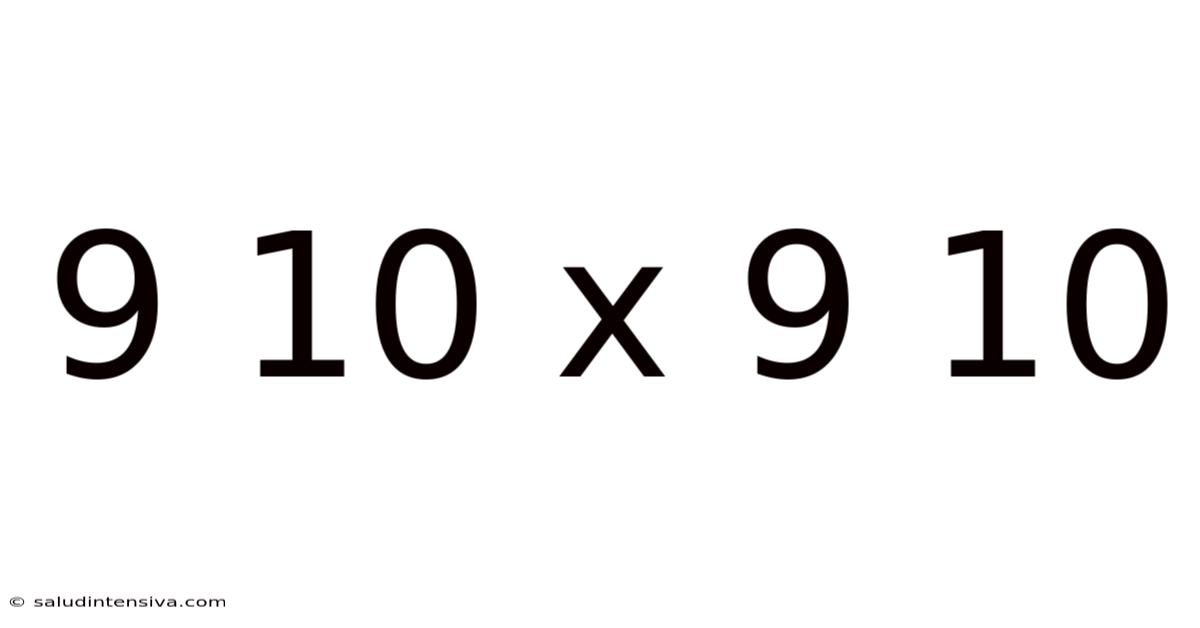
Table of Contents
Decoding 9.10 x 9.10: A Deep Dive into Decimal Multiplication and its Applications
This article explores the seemingly simple calculation of 9.10 x 9.10, but delves far beyond the immediate answer. We'll unpack the underlying principles of decimal multiplication, examine different methods for solving it, explore its applications in various fields, and address common misconceptions. Understanding this seemingly basic calculation provides a strong foundation for more complex mathematical concepts and real-world problem-solving. This comprehensive guide is suitable for students, educators, and anyone interested in improving their numerical literacy.
Understanding Decimal Numbers
Before diving into the multiplication, let's refresh our understanding of decimal numbers. A decimal number is a number that contains a decimal point, separating the whole number part from the fractional part. For instance, in 9.10, '9' represents the whole number part and '.10' represents the fractional part (equivalent to 10/100 or 1/10). The position of each digit relative to the decimal point determines its value. Moving to the right of the decimal point, the place values are tenths, hundredths, thousandths, and so on.
This understanding is crucial for performing operations like multiplication with decimals. We cannot simply ignore the decimal point; its position dictates the precision and magnitude of the result.
Methods for Calculating 9.10 x 9.10
Several methods exist for calculating 9.10 x 9.10. We'll explore three common approaches:
1. Traditional Long Multiplication
This method involves treating the decimal numbers as whole numbers, performing the multiplication, and then adjusting the position of the decimal point in the final answer.
-
Step 1: Ignore the decimal points and multiply 910 by 910.
- 910 x 910 = 828100
-
Step 2: Count the total number of decimal places in the original numbers. In 9.10 x 9.10, there are a total of four decimal places (two in each number).
-
Step 3: Place the decimal point in the product (828100) so that there are four decimal places from the right. This results in 82.8100, which simplifies to 82.81.
Therefore, 9.10 x 9.10 = 82.81
2. Using Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can use this property to break down the multiplication into simpler steps:
-
Rewrite 9.10 as (9 + 0.10)
-
Then, (9 + 0.10) x (9 + 0.10) can be expanded using the distributive property:
- 9 x 9 = 81
- 9 x 0.10 = 0.90
- 0.10 x 9 = 0.90
- 0.10 x 0.10 = 0.01
-
Adding the results together: 81 + 0.90 + 0.90 + 0.01 = 82.81
3. Using a Calculator
The simplest and often fastest method is to use a calculator. Simply input "9.10 x 9.10" and the calculator will provide the answer: 82.81. While this method is convenient, understanding the underlying principles is crucial for problem-solving in situations where a calculator isn't available.
Applications of Decimal Multiplication
Decimal multiplication isn't just a classroom exercise; it has numerous real-world applications across various fields:
-
Finance: Calculating interest, discounts, taxes, and profits all involve decimal multiplication. For example, calculating the total cost of an item after adding a sales tax or determining the final price after applying a discount.
-
Engineering: Engineers frequently use decimal multiplication in calculations involving dimensions, measurements, and material quantities. Precision is paramount, and decimals allow for accurate representation of these values. The design of buildings, bridges, and other structures relies heavily on precise calculations.
-
Science: Many scientific measurements and calculations involve decimal numbers. For example, calculating the volume of a solution, determining the speed of an object, or converting units of measurement.
-
Everyday Life: From calculating the total cost of groceries to determining the amount of paint needed for a project, decimal multiplication is a regular part of everyday life.
-
Computer Science: Decimal numbers and their manipulation are fundamental to computer programming and data representation, influencing everything from graphics rendering to financial modeling within software applications.
Addressing Common Misconceptions
Several misconceptions surround decimal multiplication:
-
Ignoring the decimal point: This leads to incorrect answers. The position of the decimal point is crucial and must be considered throughout the calculation.
-
Rounding errors: When rounding off intermediate results, cumulative errors can accumulate, leading to inaccurate final answers. It's best to avoid premature rounding wherever possible and round only at the final step if necessary.
-
Difficulty with multiple decimal places: While working with numerous decimal places can seem daunting, the fundamental principles remain the same; treat the numbers as whole numbers during multiplication, then adjust the decimal point accordingly.
Scientific Explanation: Understanding the Algorithm
The multiplication of decimal numbers relies on the fundamental principles of multiplication and place value. When we multiply 9.10 by 9.10, we're essentially breaking it down into the sum of several multiplications:
- (9 + 0.1) * (9 + 0.1) = 9 * 9 + 9 * 0.1 + 0.1 * 9 + 0.1 * 0.1
This illustrates the distributive property mentioned earlier. Each term is calculated based on its place value. The algorithm involves aligning the numbers according to their place values, performing individual multiplications, and then summing the results. The final step involves precisely placing the decimal point in the final answer based on the total number of decimal places in the original numbers.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers had a different number of decimal places?
A: The process remains the same. Count the total number of decimal places in both numbers and adjust the decimal point in the final answer accordingly. For example, 9.10 x 2.5 would have a total of three decimal places in the final answer.
Q: How can I check my answer?
A: You can use a calculator to verify your answer. You can also use estimation; round the numbers to the nearest whole number and perform a quick mental calculation. This will provide a rough estimate to help assess the reasonableness of your answer.
Q: Are there any shortcuts for multiplying decimals?
A: While there aren't many specific shortcuts for multiplying all decimals, understanding the properties of numbers (like the distributive property) and practicing different methods can lead to faster calculations. Familiarity with common decimal equivalents (like 0.25 = 1/4) can also streamline the process.
Q: Why is it important to learn decimal multiplication?
A: Decimal multiplication is a fundamental skill applicable across many disciplines and aspects of daily life. It builds a solid foundation for more advanced mathematical concepts and real-world problem-solving. Mastering it improves numerical literacy and enhances problem-solving abilities.
Conclusion
Calculating 9.10 x 9.10, while seemingly simple, serves as a gateway to understanding fundamental mathematical concepts and their real-world relevance. By understanding the various methods, appreciating the underlying principles, and addressing common misconceptions, we can move beyond rote calculation and develop a deeper appreciation for the power and application of decimal multiplication. This knowledge forms a crucial building block for success in numerous academic and professional endeavors. The ability to perform accurate decimal multiplication translates directly into confident and accurate problem-solving across a broad spectrum of applications.
Latest Posts
Latest Posts
-
5 1 4 As A Decimal
Sep 11, 2025
-
What Is 2 3 Of 5
Sep 11, 2025
-
300 000 Minutes To Hours
Sep 11, 2025
-
3 1 2 1 2
Sep 11, 2025
-
Gcf Of 32 And 36
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 9 10 X 9 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.