What Is 2/3 Of 5
saludintensiva
Sep 11, 2025 · 5 min read
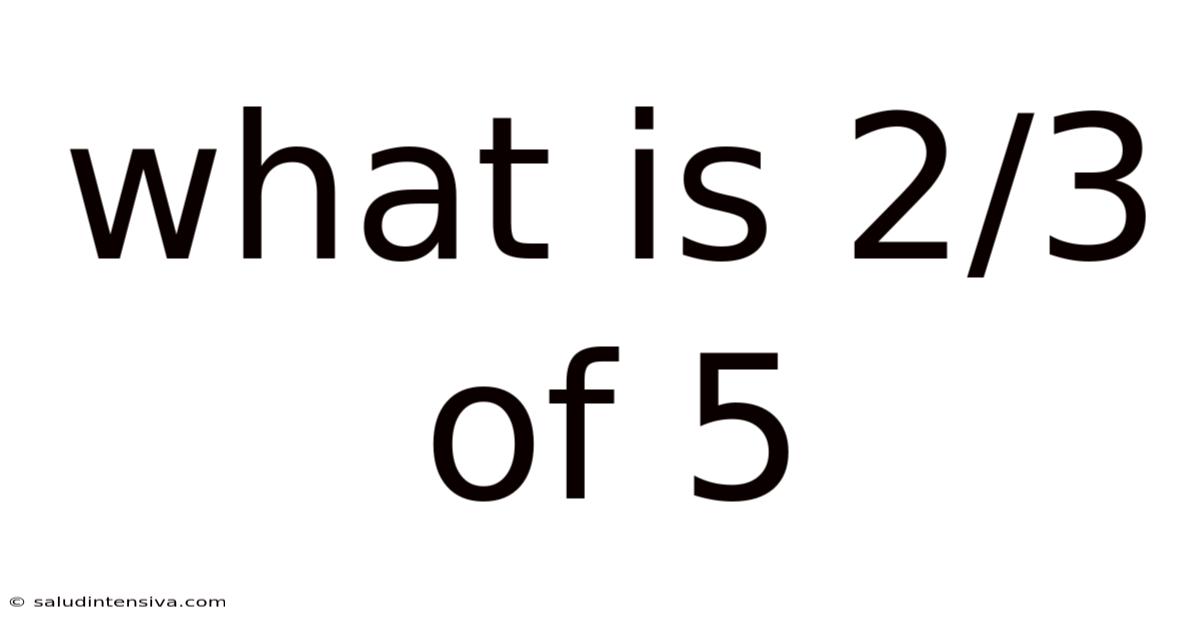
Table of Contents
What is 2/3 of 5? A Deep Dive into Fractions and Multiplication
Finding 2/3 of 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic question unlocks a deeper comprehension of fractions, multiplication, and their real-world applications. This article will not only show you how to calculate 2/3 of 5 but will also explore the underlying concepts, offer various approaches to solving the problem, and delve into the broader mathematical principles involved. This comprehensive guide will equip you with the knowledge to confidently tackle similar problems and appreciate the elegance of fractional arithmetic.
Understanding Fractions: The Building Blocks
Before we dive into calculating 2/3 of 5, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number (in this case, 2) indicates how many parts we're considering.
- Denominator: The bottom number (in this case, 3) indicates the total number of equal parts the whole is divided into.
Therefore, 2/3 means we're dealing with 2 out of 3 equal parts. Visualizing this with a simple pie chart can be very helpful. Imagine a pie cut into three equal slices. 2/3 of the pie represents two of those slices.
Method 1: Converting to Decimal Multiplication
One straightforward method to calculate 2/3 of 5 involves converting the fraction to its decimal equivalent. To do this, we simply divide the numerator by the denominator:
2 ÷ 3 ≈ 0.666666... (this is a recurring decimal)
Now, we can multiply this decimal by 5:
0.666666... × 5 ≈ 3.333333...
Therefore, 2/3 of 5 is approximately 3.333. The ellipsis (...) indicates that the decimal continues infinitely. In practical applications, you'd likely round this to a suitable level of precision, depending on the context. For example, if you're dealing with money, you might round to two decimal places (3.33).
Method 2: Direct Multiplication of Fractions
Another approach avoids decimal conversion altogether. We can directly multiply the fraction 2/3 by the whole number 5. To do this, we first need to represent 5 as a fraction: 5/1. Now, we can multiply the two fractions:
(2/3) × (5/1) = (2 × 5) / (3 × 1) = 10/3
This gives us the improper fraction 10/3. To convert this to a mixed number (a whole number and a fraction), we perform the division:
10 ÷ 3 = 3 with a remainder of 1
This translates to 3 and 1/3. So, 2/3 of 5 is equal to 3 and 1/3. This is the exact answer, unlike the approximate decimal we obtained in Method 1.
Method 3: Finding a Third, Then Doubling
This method offers a more intuitive approach, particularly helpful for those less comfortable with formal fraction manipulation.
-
Find one-third: To find one-third of 5, we divide 5 by 3: 5 ÷ 3 ≈ 1.666666...
-
Double the result: Since we want two-thirds, we double the result from step 1: 1.666666... × 2 ≈ 3.333333...
This method, while seemingly simpler, provides the same approximate decimal answer as Method 1. It highlights that finding a fraction of a number can be broken down into smaller, more manageable steps.
Real-World Applications: Where Fractions Matter
The ability to calculate fractions of numbers isn't just an academic exercise. It finds practical application in numerous everyday situations:
-
Cooking: Recipes often call for fractional amounts of ingredients (e.g., 2/3 cup of sugar).
-
Shopping: Sales discounts are frequently expressed as fractions (e.g., 1/3 off).
-
Construction: Accurate measurements in building and carpentry require a firm grasp of fractions and their manipulation.
-
Finance: Understanding interest rates, loan calculations, and profit margins often involves working with fractions and percentages (which are essentially fractions expressed as hundredths).
Extending the Concept: Working with Different Fractions and Numbers
The methods described above can be extended to calculate any fraction of any number. For example, to find 3/4 of 7:
-
Decimal Method: Convert 3/4 to a decimal (0.75), then multiply by 7 (0.75 × 7 = 5.25).
-
Direct Fraction Multiplication: Multiply (3/4) × (7/1) = 21/4 = 5 and 1/4.
-
Finding a Quarter, Then Tripling: Divide 7 by 4 (1.75), then multiply by 3 (1.75 × 3 = 5.25).
Remember to always choose the method you find most comfortable and efficient. The important takeaway is understanding the underlying principles of fraction multiplication.
Frequently Asked Questions (FAQ)
Q: What if the fraction and the number aren't easily divisible?
A: Even if the division doesn't result in a whole number, you can still use the methods described above. You might end up with a decimal answer or an improper fraction that needs converting to a mixed number.
Q: Are there other ways to solve this problem?
A: While the methods discussed are the most common and straightforward, more advanced mathematical techniques could be employed, especially for more complex fraction problems. These often involve simplifying fractions before multiplication or using algebraic approaches.
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to mathematics and have wide-ranging applications in many fields, making them crucial for problem-solving and critical thinking. Mastering them lays a strong foundation for more advanced mathematical concepts.
Conclusion: Mastering Fractions, Mastering Numbers
Calculating 2/3 of 5, while seemingly trivial, opens a doorway to a deeper understanding of fractional arithmetic. Through various approaches – decimal conversion, direct fraction multiplication, and the intuitive "find a third, then double" method – we've demonstrated several paths to the same solution. Remember that the choice of method depends on individual preference and the complexity of the problem. The real value lies in grasping the underlying principles and appreciating the power and versatility of fractions in solving real-world problems. From recipes to finances, fractions are essential tools that empower us to navigate the quantitative aspects of our daily lives. Continue practicing, explore different methods, and soon you’ll find yourself confidently tackling any fraction problem that comes your way.
Latest Posts
Latest Posts
-
Gcf Of 32 And 40
Sep 11, 2025
-
Equivalent Fractions For 8 12
Sep 11, 2025
-
Fractions Equivalent To 4 12
Sep 11, 2025
-
Gcf Of 15 And 6
Sep 11, 2025
-
Whats 15 Percent Of 25
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.