9 13 As A Decimal
saludintensiva
Sep 13, 2025 · 6 min read
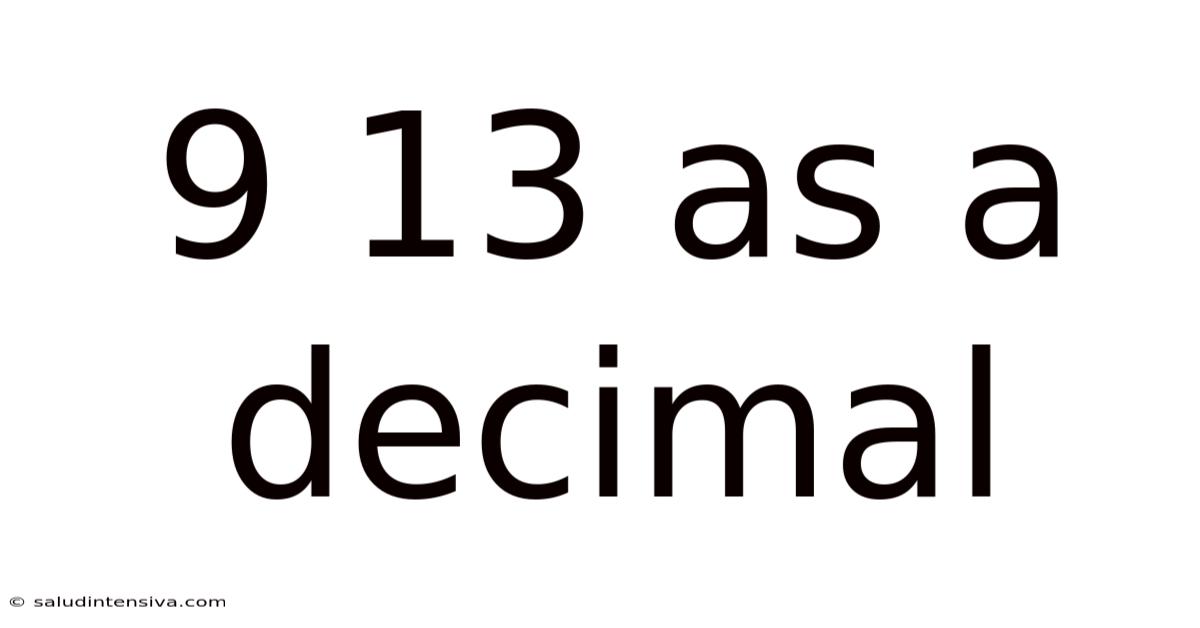
Table of Contents
Decoding 9/13: A Comprehensive Guide to Converting Fractions to Decimals
The seemingly simple task of converting a fraction like 9/13 into a decimal can open a window into the fascinating world of mathematics. Understanding this conversion not only helps with basic arithmetic but also provides a foundation for more advanced concepts in algebra, calculus, and even computer science. This article will provide a comprehensive guide to understanding the decimal representation of 9/13, exploring various methods, explaining the underlying principles, and answering frequently asked questions. We'll delve into the nature of repeating decimals, the concept of long division, and the practical applications of this knowledge. By the end, you'll not only know the decimal equivalent of 9/13 but also possess a deeper understanding of fractional and decimal representation.
Understanding Fractions and Decimals
Before diving into the specifics of 9/13, let's establish a firm grasp of the basic concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, represents a number using a base-10 system. It uses a decimal point to separate the whole number part from the fractional part. Each digit to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, and so on).
Converting a fraction to a decimal essentially means expressing the fractional part of the whole as a decimal representation.
Method 1: Long Division
The most straightforward method for converting 9/13 to a decimal is through long division. This method involves dividing the numerator (9) by the denominator (13).
-
Set up the long division: Write 9 as the dividend (inside the division symbol) and 13 as the divisor (outside the division symbol).
-
Add a decimal point and zeros: Since 9 is smaller than 13, we add a decimal point to the quotient (the result) and append zeros to the dividend. This doesn't change the value of the fraction, allowing us to continue the division.
-
Perform the division: Start dividing 13 into 90. 13 goes into 90 six times (13 x 6 = 78). Subtract 78 from 90, leaving a remainder of 12.
-
Bring down the next zero: Bring down the next zero from the dividend to make 120.
-
Repeat the process: Divide 13 into 120. 13 goes into 120 nine times (13 x 9 = 117). Subtract 117 from 120, leaving a remainder of 3.
-
Continue the pattern: This process will continue indefinitely. You'll notice that the remainders repeat in a cycle. This indicates that the decimal representation of 9/13 is a repeating decimal.
Following this process, you'll find that the decimal representation of 9/13 is approximately 0.692307692307... The sequence "692307" repeats infinitely.
Method 2: Using a Calculator
While long division provides a deep understanding of the process, a calculator offers a quicker way to find the decimal representation. Simply divide 9 by 13 using your calculator. Most calculators will display the decimal representation to a certain number of decimal places, but remember that the true value is a repeating decimal.
Understanding Repeating Decimals
The decimal representation of 9/13 is a repeating decimal, also known as a recurring decimal. This means that the digits after the decimal point repeat in a specific pattern infinitely. In the case of 9/13, the repeating block is "692307". Repeating decimals are often represented using a bar over the repeating block: 0.692307̅. This notation indicates that the sequence "692307" continues without end.
The Significance of Repeating Decimals
The occurrence of repeating decimals highlights an important relationship between fractions and decimal numbers. Not all fractions result in terminating decimals (decimals that end). Fractions with denominators that have prime factors other than 2 and 5 (the prime factors of 10) will always result in repeating decimals. Since 13 is a prime number, it's not surprising that 9/13 yields a repeating decimal.
Practical Applications
Understanding the conversion of fractions to decimals is crucial in various fields:
- Engineering and Science: Precise calculations often require decimal representations.
- Finance: Calculating interest rates, discounts, and other financial calculations frequently involves decimals.
- Computer Science: Representing numbers in binary format (used in computers) often involves converting between fractions and decimals.
- Everyday Life: Many everyday calculations, such as calculating percentages or splitting bills, rely on a sound understanding of decimals.
Beyond 9/13: Generalizing the Conversion
The methods used to convert 9/13 to a decimal apply to any fraction. The process of long division remains the fundamental method. However, for fractions with large denominators, using a calculator becomes more practical. Recognizing when a fraction will produce a terminating or repeating decimal is a valuable skill acquired through understanding the prime factorization of the denominator.
Frequently Asked Questions (FAQ)
Q: Is the decimal representation of 9/13 truly infinite?
A: Yes, the decimal representation of 9/13 is infinite because the remainder never becomes zero during the long division process. The repeating block "692307" continues indefinitely.
Q: How many digits repeat in the decimal representation of 9/13?
A: Six digits (692307) repeat in the decimal representation of 9/13.
Q: Can all fractions be expressed as decimals?
A: Yes, all fractions can be expressed as decimals. However, some fractions result in terminating decimals, while others result in repeating decimals.
Q: How can I round the decimal representation of 9/13?
A: You can round the decimal representation to a desired number of decimal places. For example, rounded to three decimal places, 9/13 is approximately 0.692.
Q: What is the difference between a terminating decimal and a repeating decimal?
A: A terminating decimal has a finite number of digits after the decimal point, while a repeating decimal has an infinite number of digits that repeat in a pattern.
Conclusion
Converting the fraction 9/13 to its decimal equivalent (approximately 0.692307̅) provides a valuable opportunity to reinforce our understanding of fractions, decimals, and the long division process. The seemingly simple task reveals the intricacies of mathematical representation and the fascinating nature of repeating decimals. The ability to perform this conversion is a fundamental skill applicable across numerous disciplines and everyday situations. By mastering this process, you not only gain a practical skill but also a deeper appreciation for the elegance and interconnectedness of mathematical concepts. Remember that while calculators offer convenience, understanding the underlying principles of long division provides a robust foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
1 3 To The 2nd Power
Sep 13, 2025
-
11 30 As A Decimal
Sep 13, 2025
-
80 000 Pounds To Kg
Sep 13, 2025
-
8 10 Is Equal To
Sep 13, 2025
-
11 9 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9 13 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.