9 40 As A Percent
saludintensiva
Sep 19, 2025 · 5 min read
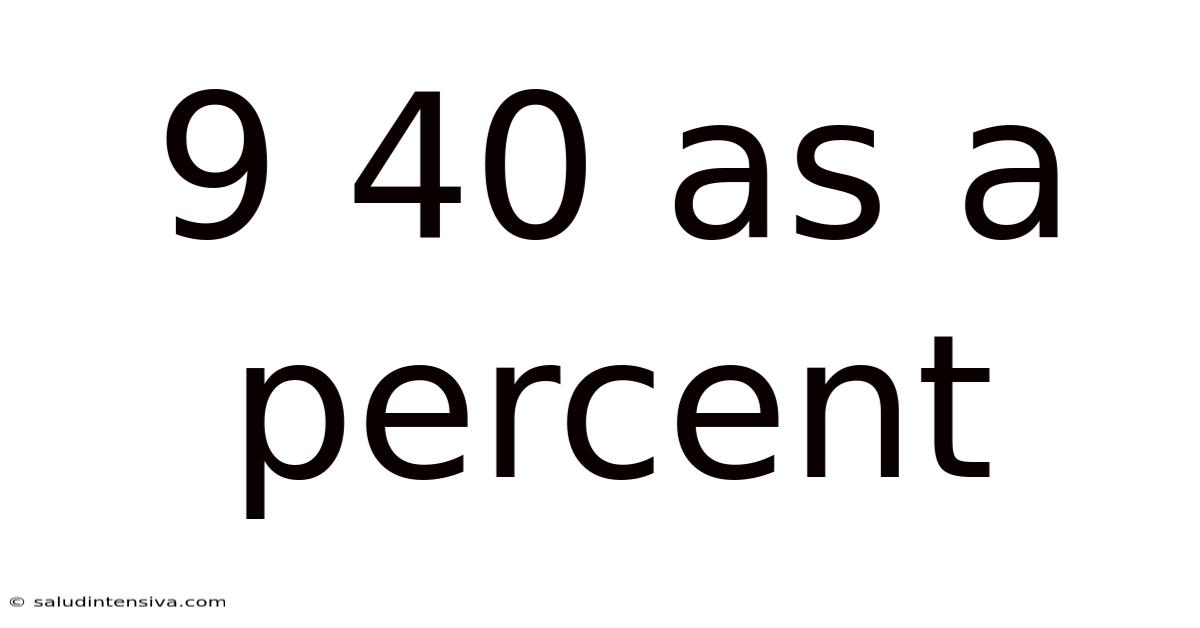
Table of Contents
9/40 as a Percent: A Comprehensive Guide to Converting Fractions to Percentages
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting the fraction 9/40 into a percentage, explaining the steps involved, providing multiple approaches, and exploring the broader concept of fractional percentages. We'll also look at practical examples and frequently asked questions to solidify your understanding.
Introduction: Understanding Fractions and Percentages
Before we dive into converting 9/40 to a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates how many parts are being considered.
A percentage, on the other hand, represents a fraction of 100. It expresses a proportion relative to a whole, indicated by the symbol '%'. Essentially, a percentage is a fraction with a denominator of 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the simplified fraction 1/2.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 9/40 to a percentage involves understanding the fundamental relationship between fractions and percentages. To convert a fraction to a percentage, we need to express the fraction as an equivalent fraction with a denominator of 100.
-
Find an equivalent fraction with a denominator of 100: We need to determine what number we can multiply 40 by to get 100. This is found by dividing 100 by 40: 100 ÷ 40 = 2.5.
-
Multiply both the numerator and the denominator by the same number: To maintain the value of the fraction, we must multiply both the numerator and the denominator by 2.5:
(9 × 2.5) / (40 × 2.5) = 22.5 / 100
-
Express the result as a percentage: Since the denominator is now 100, the numerator directly represents the percentage. Therefore, 22.5/100 is equivalent to 22.5%.
Method 2: Using Decimal Conversion as an Intermediate Step
Another approach involves converting the fraction to a decimal first and then converting the decimal to a percentage.
-
Convert the fraction to a decimal: Divide the numerator (9) by the denominator (40): 9 ÷ 40 = 0.225
-
Convert the decimal to a percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the '%' symbol: 0.225 × 100 = 22.5%
This method is particularly useful when dealing with fractions that don't easily convert to an equivalent fraction with a denominator of 100.
Method 3: Understanding Proportions and Cross-Multiplication
This method utilizes the concept of proportions. We can set up a proportion to solve for the percentage:
9/40 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
9 * 100 = 40 * x
900 = 40x
x = 900 / 40
x = 22.5
Therefore, 9/40 is equal to 22.5%. This method reinforces the underlying mathematical principles and offers a more algebraic approach to the problem.
Practical Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating discounts: If a store offers a 9/40 discount on an item, you can easily determine the percentage discount (22.5%) to calculate the final price.
-
Analyzing statistical data: Representing data as percentages allows for easier comparison and interpretation. For instance, if 9 out of 40 students passed an exam, the pass rate is 22.5%.
-
Understanding financial reports: Financial statements often use percentages to represent proportions of income, expenses, and profits.
-
Calculating tax rates: Tax rates are frequently expressed as percentages, allowing for easy calculation of tax amounts based on income or purchase price.
-
Measuring progress towards a goal: Tracking progress on a project or goal can be simplified by expressing completion as a percentage. For example, completing 9 out of 40 tasks represents 22.5% completion.
Further Exploration: Working with More Complex Fractions
While we focused on 9/40, the methods outlined above can be applied to any fraction. Even more complex fractions, involving larger numbers or mixed numbers (a whole number and a fraction), can be converted to percentages using the same fundamental principles:
-
Convert mixed numbers to improper fractions: A mixed number like 1 1/4 should be converted to the improper fraction 5/4 before proceeding with the conversion to a percentage.
-
Simplify fractions where possible: Simplifying a fraction before converting to a percentage can make the calculation easier. For example, 10/20 simplifies to 1/2, which is easily converted to 50%.
-
Use a calculator for larger numbers: For very large numbers, a calculator can help with the division and multiplication steps involved in the conversion process.
Frequently Asked Questions (FAQ)
-
Q: Can a fraction ever result in a percentage greater than 100%?
- A: Yes, if the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This indicates that the fraction represents a value more than the whole.
-
Q: What if I get a repeating decimal when converting the fraction?
- A: You can either round the decimal to a certain number of decimal places before converting to a percentage, or express the percentage using the repeating decimal (e.g., 33.333...%).
-
Q: Are there other ways to express a proportion besides fractions and percentages?
- A: Yes, proportions can also be expressed as ratios (e.g., 9:40) or decimals (e.g., 0.225).
-
Q: Why is it important to learn how to convert fractions to percentages?
- A: Understanding this conversion is fundamental for interpreting data, making calculations in various fields, and understanding the relationships between different numerical representations.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a core mathematical skill with widespread applicability. By understanding the underlying principles and mastering the various methods described above – direct conversion, decimal conversion, and using proportions – you'll be well-equipped to tackle a range of problems involving fractions and percentages. Remember to practice regularly and apply these techniques to real-world scenarios to build confidence and proficiency. The ability to seamlessly convert between fractions and percentages is a valuable asset in both academic and professional settings, allowing for clearer understanding and more effective problem-solving.
Latest Posts
Latest Posts
-
9 20 To A Decimal
Sep 19, 2025
-
15 32 As A Decimal
Sep 19, 2025
-
What Is Half Of 19
Sep 19, 2025
-
Rounding To The Greatest Place
Sep 19, 2025
-
Is 2 5 Greater Than 3 8
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 9 40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.