9 50 As A Percent
saludintensiva
Sep 15, 2025 · 5 min read
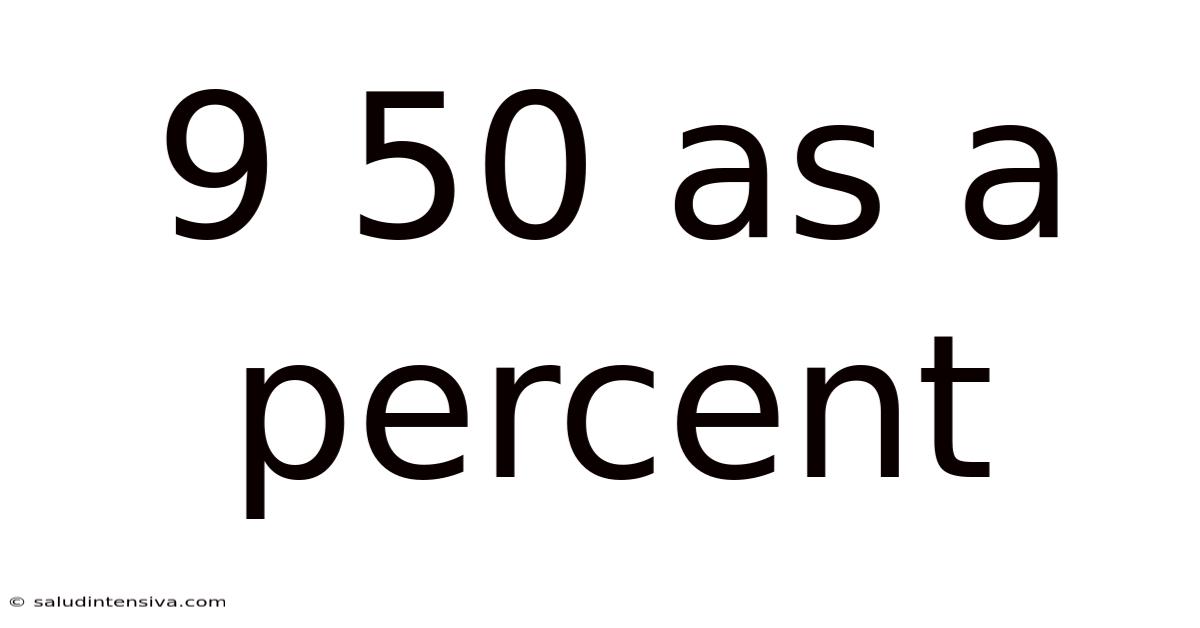
Table of Contents
Understanding 9/50 as a Percentage: A Comprehensive Guide
What is 9/50 as a percentage? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with widespread applications in everyday life, from calculating discounts to understanding financial reports. This article will guide you through the process of converting 9/50 into a percentage, explain the underlying principles, and provide additional examples to solidify your understanding. We'll also explore the practical applications of percentage calculations.
Understanding Fractions, Decimals, and Percentages
Before diving into the conversion, let's review the core concepts. A fraction represents a part of a whole. In the fraction 9/50, 9 is the numerator (the part) and 50 is the denominator (the whole). A decimal is a way of expressing a fraction using a base-ten system, with a decimal point separating the whole number from the fractional part. A percentage is a fraction expressed as a portion of 100, represented by the symbol %.
The relationship between these three is crucial: a fraction can be converted to a decimal by dividing the numerator by the denominator; a decimal can be converted to a percentage by multiplying by 100; and a percentage can be converted to a fraction by dividing by 100 and simplifying.
Converting 9/50 to a Percentage: Step-by-Step
Here's how to convert the fraction 9/50 to a percentage:
Step 1: Divide the numerator by the denominator.
9 ÷ 50 = 0.18
Step 2: Multiply the decimal result by 100.
0.18 x 100 = 18
Step 3: Add the percentage symbol.
18%
Therefore, 9/50 is equal to 18%.
Alternative Method: Finding an Equivalent Fraction
Another approach involves finding an equivalent fraction with a denominator of 100. Since percentages are parts of 100, this method simplifies the conversion.
We need to find a number that, when multiplied by 50, gives us 100. That number is 2 (50 x 2 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number.
(9 x 2) / (50 x 2) = 18/100
Since 18/100 means 18 out of 100, this directly translates to 18%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
-
Financial Literacy: Calculating interest rates, discounts, taxes, tips, and profit margins all involve percentages. For instance, a 10% discount on a $100 item means a savings of $10 (10% of $100).
-
Data Analysis: Percentages are used extensively in presenting statistical data, making it easier to understand and compare different sets of information. For example, expressing survey results as percentages makes it simpler to grasp public opinion.
-
Scientific Calculations: Percentages are used in many scientific fields, such as chemistry (concentration of solutions), biology (population growth rates), and physics (efficiency of machines).
-
Everyday Life: Calculating sale prices, understanding nutritional information (percentage of daily value), or determining the percentage of completion of a project all involve percentage calculations.
Further Examples and Practice
Let's work through a few more examples to reinforce the concept:
-
Convert 15/25 to a percentage:
- 15 ÷ 25 = 0.6
- 0.6 x 100 = 60
- 60%
-
Convert 2/5 to a percentage:
- 2 ÷ 5 = 0.4
- 0.4 x 100 = 40
- 40%
-
Convert 3/4 to a percentage:
- 3 ÷ 4 = 0.75
- 0.75 x 100 = 75
- 75%
These examples demonstrate the consistent application of the steps involved in converting fractions to percentages.
Converting Percentages to Fractions and Decimals
The process can be reversed. Let's convert 18% back to a fraction and a decimal:
-
Percentage to Decimal: Divide the percentage by 100. 18% ÷ 100 = 0.18
-
Percentage to Fraction: Write the percentage as a fraction with a denominator of 100, and then simplify. 18/100 can be simplified by dividing both numerator and denominator by their greatest common divisor, which is 2. This simplifies to 9/50.
Dealing with More Complex Fractions
While the examples above involved relatively straightforward fractions, the principles remain the same even with more complex fractions. For instance, converting a fraction like 27/150 to a percentage involves the same steps:
- Divide the numerator by the denominator: 27 ÷ 150 ≈ 0.18
- Multiply the decimal by 100: 0.18 x 100 = 18
- Add the percentage symbol: 18%
Note that in this case, the result is an approximate percentage due to the decimal approximation in step 1.
Frequently Asked Questions (FAQ)
Q: What if the fraction results in a repeating decimal?
A: Sometimes, dividing the numerator by the denominator results in a repeating decimal (e.g., 1/3 = 0.333...). In such cases, you can either round the decimal to a certain number of decimal places before multiplying by 100 or express the percentage as a fraction.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have functions that allow you to perform these calculations directly. Simply divide the numerator by the denominator and then multiply the result by 100.
Q: What are some common real-world applications of this knowledge?
A: Calculating discounts in stores, understanding interest rates on loans, interpreting statistical data presented as percentages, determining tax rates, and calculating tips in restaurants are all examples of everyday applications.
Q: Is there a quick way to estimate percentages?
A: For quick estimations, you can round the numbers to make the calculations easier. For example, instead of calculating 17/52 as a percentage precisely, you could approximate it as 17/50, which is easier to work with.
Conclusion
Converting 9/50 to a percentage, which equals 18%, is a straightforward process that highlights the fundamental relationship between fractions, decimals, and percentages. Mastering this conversion is crucial for various aspects of life, from managing personal finances to interpreting data and solving real-world problems. Understanding the underlying principles and practicing with different examples will build your confidence and proficiency in working with these essential mathematical concepts. Remember to apply these skills in everyday situations to further strengthen your understanding and make these calculations second nature.
Latest Posts
Latest Posts
-
Lcm For 7 And 11
Sep 15, 2025
-
What Percent Is 5 8
Sep 15, 2025
-
6 To The Fifth Power
Sep 15, 2025
-
Lcm Of 14 And 16
Sep 15, 2025
-
Lcm Of 3 9 15
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 9 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.