90 Percent As A Decimal
saludintensiva
Sep 14, 2025 · 5 min read
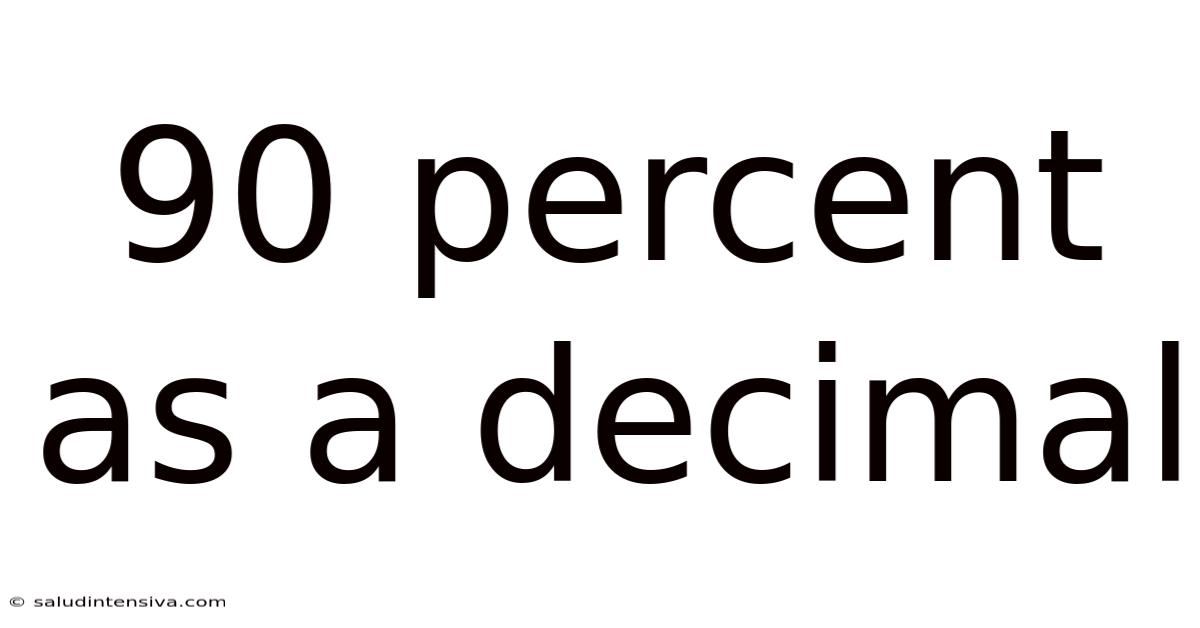
Table of Contents
90 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and has wide-ranging applications in various fields, from finance and statistics to everyday life. This comprehensive guide will explore the conversion of 90 percent to its decimal form, providing a detailed explanation of the process and exploring related concepts. We'll delve into the underlying principles, offer practical examples, and address frequently asked questions to ensure a thorough understanding of this important mathematical concept.
Introduction: Percentages and Decimals
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Decimals, on the other hand, represent numbers as fractions with a denominator that is a power of 10 (e.g., 10, 100, 1000). Converting between percentages and decimals is a crucial skill in many mathematical operations. This article focuses specifically on converting 90 percent to its decimal equivalent and exploring the broader implications of this conversion.
Converting 90 Percent to a Decimal: The Method
The conversion of a percentage to a decimal is a straightforward process. The key is to remember that a percentage is simply a fraction with a denominator of 100. Therefore, to convert a percentage to a decimal, you divide the percentage by 100.
Step-by-step process for converting 90% to a decimal:
-
Write the percentage as a fraction: 90% can be written as 90/100.
-
Divide the numerator by the denominator: 90 ÷ 100 = 0.9
Therefore, 90 percent as a decimal is 0.9.
Understanding the Underlying Principles
The conversion process relies on the fundamental relationship between percentages and decimals. A percentage represents a proportion, and a decimal represents the same proportion expressed as a fraction of 1. Dividing by 100 effectively scales the percentage down to its decimal equivalent. This is because dividing by 100 is the same as moving the decimal point two places to the left.
Consider the number 90. The decimal point is implicitly located at the end (90.), even if it's not shown. When we divide by 100, we move this decimal point two places to the left: 90. becomes 0.90, or simply 0.9. This method works for any percentage conversion.
Practical Applications of 90% as a Decimal (0.9)
The decimal equivalent of 90%, 0.9, has numerous applications in various fields. Here are a few examples:
-
Finance: Calculating interest, discounts, or profit margins often involves using percentages and their decimal equivalents. For example, if a store offers a 90% discount on an item, you can calculate the discount amount by multiplying the original price by 0.9.
-
Statistics: Probabilities are frequently expressed as percentages and then converted to decimals for calculations. A 90% probability of an event occurring translates to a probability of 0.9.
-
Science: In scientific experiments, data is often presented as percentages, and for further calculations, converting them into decimals is necessary. This allows for consistent application of mathematical operations.
-
Everyday Life: Many everyday scenarios involve percentages. For example, if you correctly answered 90% of questions on a test, your score can be represented as 0.9 or 9/10.
These are just a few examples. The ability to seamlessly convert between percentages and decimals enables efficient and accurate calculations in countless situations.
Further Exploration: Working with Percentages and Decimals
Beyond the simple conversion of 90%, understanding how to work with percentages and decimals is crucial. Here are some related concepts and examples:
-
Converting Decimals to Percentages: The reverse process is equally important. To convert a decimal to a percentage, you multiply the decimal by 100 and add a "%" sign. For instance, 0.75 * 100 = 75%, and 0.2 * 100 = 20%.
-
Calculating Percentages of Numbers: To find a percentage of a number, convert the percentage to a decimal and then multiply it by the number. For example, 90% of 50 is calculated as 0.9 * 50 = 45.
-
Finding the Percentage One Number is of Another: To find what percentage one number is of another, divide the first number by the second, and then multiply the result by 100 to express it as a percentage. For example, to find what percentage 45 is of 50, you calculate (45/50) * 100 = 90%.
-
Working with Fractions, Decimals, and Percentages: It's crucial to be comfortable converting between fractions, decimals, and percentages. All three represent proportions, and the ability to switch between them allows for flexibility in solving various problems.
These skills are essential for success in various academic and professional settings.
Addressing Frequently Asked Questions (FAQ)
Q1: Why is it important to understand the conversion between percentages and decimals?
A1: The ability to convert between percentages and decimals is essential for performing mathematical calculations involving proportions. Many real-world problems require this conversion for accurate solutions. It streamlines calculations and enhances understanding.
Q2: Are there any shortcuts for converting percentages to decimals?
A2: Yes, you can simply move the decimal point two places to the left. For example, 90% becomes 0.9. This is a quick and efficient method for this conversion.
Q3: Can I use a calculator to convert percentages to decimals?
A3: Yes, most calculators can perform this conversion directly or indirectly. Simply divide the percentage by 100. Many scientific calculators have a percent key (%) that simplifies this process even further.
Q4: What if I have a percentage with a decimal part (e.g., 90.5%)?
A4: The same principle applies. Divide the percentage by 100. 90.5% divided by 100 equals 0.905.
Q5: How can I improve my understanding of percentages and decimals?
A5: Practice regularly. Solve various problems that involve converting between percentages, decimals, and fractions. Utilize online resources, textbooks, or educational apps that provide exercises and explanations. The more you practice, the more comfortable you'll become.
Conclusion: Mastering the Conversion of 90 Percent to a Decimal
This guide has comprehensively explained the conversion of 90 percent to its decimal equivalent, 0.9. We've explored the underlying principles, provided practical examples, and addressed frequently asked questions. The ability to seamlessly convert between percentages and decimals is a fundamental skill with wide-ranging applications. Mastering this skill will significantly enhance your mathematical proficiency and provide a solid foundation for tackling more complex problems across various fields. Remember, the key is to practice regularly and apply this knowledge in different contexts to reinforce your understanding. The more you use this skill, the more natural and intuitive it will become. By understanding this fundamental mathematical concept, you'll be better equipped to handle numerous real-world situations effectively.
Latest Posts
Latest Posts
-
6 Divided By 1 4
Sep 14, 2025
-
Simplify As Much As Possible
Sep 14, 2025
-
Future Value Of 1 Table
Sep 14, 2025
-
4 To The Fifth Power
Sep 14, 2025
-
Convert 625 Into A Fraction
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 90 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.