Can 5 4 Be Simplified
saludintensiva
Sep 18, 2025 · 6 min read
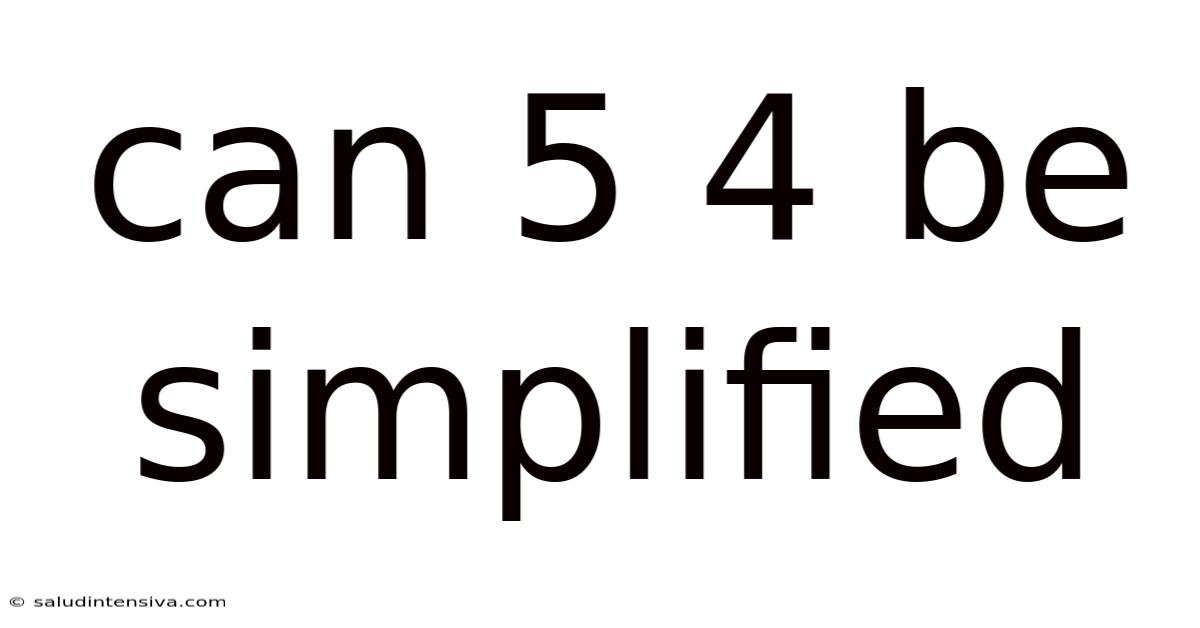
Table of Contents
Can 5/4 Be Simplified? Understanding Fraction Reduction
The question, "Can 5/4 be simplified?" might seem deceptively simple, especially for those comfortable with fractions. However, understanding the intricacies of fraction simplification goes beyond just knowing the rules; it delves into the fundamental concepts of prime factorization, greatest common divisors (GCD), and the very nature of rational numbers. This comprehensive guide will not only answer the initial question but also equip you with a deeper understanding of fraction simplification and its broader mathematical implications.
Introduction: What Does it Mean to Simplify a Fraction?
Simplifying a fraction, also known as reducing a fraction to its simplest form, means expressing the fraction using the smallest possible whole numbers in the numerator and denominator while maintaining the fraction's value. This is achieved by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In essence, we're finding the equivalent fraction with the least common terms.
Can 5/4 Be Simplified? The Answer and the Why
The answer is no, 5/4 cannot be simplified further. Let's explore why.
To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator (5) and the denominator (4). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
- Finding the GCD: The factors of 5 are 1 and 5. The factors of 4 are 1, 2, and 4. The only common factor between 5 and 4 is 1.
Since the GCD of 5 and 4 is 1, dividing both the numerator and the denominator by 1 doesn't change the fraction's value. Therefore, 5/4 is already in its simplest form.
Understanding Prime Factorization and its Role in Simplification
Prime factorization is a crucial tool in simplifying fractions, particularly when dealing with larger numbers. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). Let's illustrate this with an example:
Consider the fraction 12/18.
- Prime Factorize the Numerator (12): 12 = 2 x 2 x 3 = 2² x 3
- Prime Factorize the Denominator (18): 18 = 2 x 3 x 3 = 2 x 3²
Now, we can rewrite the fraction as: (2² x 3) / (2 x 3²)
Notice that both the numerator and the denominator share a common factor: 2 x 3 = 6. Dividing both the numerator and denominator by 6, we get:
(2² x 3) / (2 x 3²) = (2 x 3 x 2) / (2 x 3 x 3) = 2/3
Therefore, 12/18 simplifies to 2/3. This method clearly showcases how prime factorization helps identify the GCD and simplifies the reduction process.
The Concept of Greatest Common Divisor (GCD)
The GCD, as mentioned earlier, is the largest number that divides both the numerator and the denominator without leaving a remainder. Finding the GCD is essential for simplifying fractions efficiently. There are several ways to find the GCD:
-
Listing Factors: This method involves listing all the factors of both the numerator and the denominator and identifying the largest common factor. This works well for smaller numbers but becomes cumbersome for larger ones.
-
Prime Factorization: This is a more efficient method for larger numbers, as described in the previous section. By finding the prime factors, you can easily identify the common factors and their product, which is the GCD.
-
Euclidean Algorithm: This is a more advanced algorithm for finding the GCD, particularly useful for very large numbers. It involves a series of divisions until the remainder is 0. The last non-zero remainder is the GCD.
Improper Fractions and Mixed Numbers: A Deeper Dive
The fraction 5/4 is an improper fraction because the numerator (5) is larger than the denominator (4). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 5/4 to a mixed number:
- Divide the numerator (5) by the denominator (4): 5 ÷ 4 = 1 with a remainder of 1.
- The whole number part of the mixed number is the quotient (1).
- The fractional part of the mixed number is the remainder (1) over the denominator (4): 1/4.
Therefore, 5/4 is equivalent to the mixed number 1 1/4. While converting to a mixed number doesn't simplify the fraction in terms of reducing it to lower terms, it provides a different way to represent the same value.
Practical Applications of Fraction Simplification
Simplifying fractions is not just a theoretical exercise; it has numerous practical applications in various fields:
-
Measurement and Engineering: Simplifying fractions is crucial in precise measurements, calculations in engineering designs, and other fields requiring accuracy.
-
Cooking and Baking: Recipes often use fractions, and simplifying them makes it easier to understand and measure ingredients.
-
Finance and Accounting: Calculations involving percentages, interest rates, and financial ratios often involve fractions that need simplification for clarity and accuracy.
-
Data Analysis and Statistics: Simplifying fractions helps in understanding and interpreting data more efficiently.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, work with, and compare. It also presents the value in the most concise and efficient way.
Q2: Can I simplify a fraction by just dividing the numerator and denominator by any common factor?
A2: Yes, but for the simplest form, you must divide by the greatest common factor (GCD). Dividing by any smaller common factor will result in a simplified fraction, but it won't be in its simplest form.
Q3: What if the GCD of the numerator and denominator is the numerator itself?
A3: In this case, the fraction simplifies to a whole number. For example, 6/3 simplifies to 2 because the GCD of 6 and 3 is 3.
Q4: Are there any shortcuts for simplifying fractions?
A4: While prime factorization is generally recommended, for simple fractions, you can sometimes visually identify common factors and divide accordingly. However, always double-check to ensure you've found the GCD.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics with far-reaching applications. Understanding the concepts of prime factorization, GCD, and the different methods for finding the GCD is crucial for mastering this skill. While 5/4 cannot be simplified because its GCD is 1, understanding the process allows you to tackle more complex fractions with confidence. The ability to simplify fractions efficiently enhances mathematical proficiency and provides a solid foundation for tackling more advanced mathematical concepts. Remember, practice is key; the more you work with fractions, the more intuitive the process of simplification will become.
Latest Posts
Latest Posts
-
Multiples Of 7 And 8
Sep 18, 2025
-
39 7 Degrees Celsius To Fahrenheit
Sep 18, 2025
-
What Is 12 9 Simplified
Sep 18, 2025
-
How Long Is 720 Minutes
Sep 18, 2025
-
Convert 54 F To Celsius
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Can 5 4 Be Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.