Equivalent Fraction Of 7 9
saludintensiva
Sep 10, 2025 · 6 min read
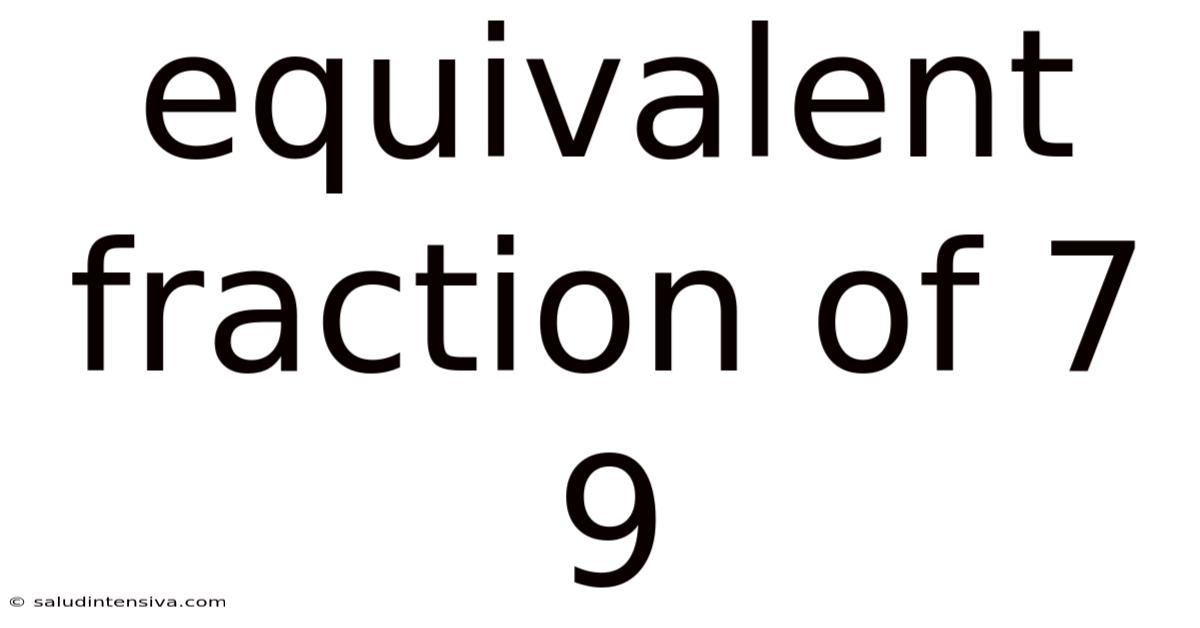
Table of Contents
Unveiling the World of Equivalent Fractions: A Deep Dive into 7/9
Finding equivalent fractions might seem like a simple task, but understanding the underlying principles unlocks a deeper appreciation for fractions and their role in mathematics. This comprehensive guide delves into the concept of equivalent fractions, using 7/9 as a prime example. We'll explore various methods for finding equivalent fractions, explain the underlying mathematical reasoning, and address frequently asked questions. By the end, you'll not only be able to find equivalent fractions for 7/9 but also possess a solid understanding of the broader concept.
Understanding Fractions: A Quick Refresher
Before we dive into equivalent fractions, let's briefly revisit the fundamental concept of a fraction. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 7/9, 7 is the numerator and 9 is the denominator. This means we have 7 parts out of a total of 9 equal parts.
What are Equivalent Fractions?
Equivalent fractions are fractions that represent the same value, even though they look different. They're essentially different ways of expressing the same proportion or part of a whole. Think of it like using different units to measure the same length – centimeters and inches, for instance. Both represent the same length, just in different units. Similarly, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half of a whole.
Our focus here is to find equivalent fractions for 7/9. This means we're looking for fractions that, despite having different numerators and denominators, represent exactly the same proportion as 7/9.
Methods for Finding Equivalent Fractions of 7/9
There are several methods for finding equivalent fractions. The most common and fundamental method involves multiplying or dividing both the numerator and the denominator by the same non-zero number. This is based on the fundamental principle that multiplying or dividing both parts of a fraction by the same number does not change its overall value.
Method 1: Multiplying the Numerator and Denominator
This is the simplest method. We can find an equivalent fraction by multiplying both the numerator (7) and the denominator (9) by the same whole number. Let's try a few examples:
- Multiply by 2: (7 x 2) / (9 x 2) = 14/18
- Multiply by 3: (7 x 3) / (9 x 3) = 21/27
- Multiply by 4: (7 x 4) / (9 x 4) = 28/36
- Multiply by 5: (7 x 5) / (9 x 5) = 35/45
- Multiply by 10: (7 x 10) / (9 x 10) = 70/90
All of these fractions – 14/18, 21/27, 28/36, 35/45, and 70/90 – are equivalent to 7/9. We can continue this process indefinitely, generating an infinite number of equivalent fractions.
Method 2: Dividing the Numerator and Denominator (Simplification)
While the previous method generates larger equivalent fractions, we can also find smaller equivalent fractions by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In the case of 7/9, the GCD of 7 and 9 is 1. This means 7/9 is already in its simplest form – it cannot be simplified further. This is because 7 is a prime number, meaning it's only divisible by 1 and itself.
Method 3: Visual Representation
Visualizing fractions helps solidify the concept of equivalence. Imagine a rectangular shape divided into 9 equal parts. Shading 7 of those parts represents the fraction 7/9. Now imagine dividing the same rectangle into 18 equal parts. Shading 14 of those parts would represent 14/18, which visually demonstrates its equivalence to 7/9. The proportion of shaded area remains the same, even though the number of parts has changed.
The Mathematical Rationale Behind Equivalent Fractions
The reason multiplying or dividing both the numerator and denominator by the same number works is rooted in the properties of fractions and the concept of proportionality. A fraction represents a ratio, and equivalent fractions maintain this ratio. When we multiply both the numerator and denominator by the same number (say, 'x'), we are essentially multiplying the fraction by x/x, which is equal to 1. Multiplying any number by 1 doesn't change its value. Similarly, dividing both parts by the same number is equivalent to dividing the fraction by that number, maintaining the proportionality.
Applications of Equivalent Fractions
Equivalent fractions are essential in various mathematical contexts:
-
Simplifying Fractions: Finding the simplest form of a fraction, as we did with 7/9 (which is already in its simplest form), makes calculations easier and clearer.
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, we need to find a common denominator. This often involves finding equivalent fractions with the same denominator.
-
Comparing Fractions: Determining which fraction is larger or smaller often requires finding equivalent fractions with a common denominator.
-
Solving Equations: Equivalent fractions play a vital role in solving algebraic equations involving fractions.
-
Real-World Applications: Equivalent fractions are used extensively in everyday life – from cooking (halving a recipe) to calculating proportions in construction or finance.
Frequently Asked Questions (FAQ)
Q: Can I find an infinite number of equivalent fractions for 7/9?
A: Yes, absolutely. You can multiply the numerator and denominator by any non-zero whole number to create a new equivalent fraction. This process can be repeated indefinitely, generating an infinite number of equivalent fractions.
Q: Why is 7/9 already in its simplest form?
A: 7 and 9 share only one common factor, which is 1. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. Since 7 is a prime number and doesn't divide 9 evenly (other than by 1), 7/9 is in its simplest form.
Q: What if I divide the numerator and denominator by different numbers?
A: If you divide the numerator and denominator by different numbers, you will change the value of the fraction. The key to finding equivalent fractions is to use the same number for both the numerator and the denominator.
Q: How do I find the greatest common divisor (GCD)?
A: There are several methods for finding the GCD, including listing factors, prime factorization, and the Euclidean algorithm. For smaller numbers like 7 and 9, it's relatively easy to see that their only common factor is 1. For larger numbers, using a prime factorization method or the Euclidean algorithm becomes more efficient.
Conclusion
Understanding equivalent fractions is a cornerstone of mathematical proficiency. This exploration of 7/9, while seemingly focused on a specific fraction, has provided a comprehensive framework for understanding the broader concept. The methods presented – multiplying, dividing, and visual representation – offer diverse approaches to find equivalent fractions. Remember, the key is to maintain the ratio between the numerator and denominator. By mastering the concept of equivalent fractions, you'll build a strong foundation for more advanced mathematical concepts and applications. From simplifying fractions to solving complex equations, equivalent fractions are essential tools in your mathematical arsenal.
Latest Posts
Latest Posts
-
What Time Is 15 29
Sep 10, 2025
-
What Is 15 Of 26
Sep 10, 2025
-
3 Foot By 4 Foot
Sep 10, 2025
-
Convert 1 5 Kg Into Pounds
Sep 10, 2025
-
84 Degrees Fahrenheit To Celsius
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Equivalent Fraction Of 7 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.