What Is 15 Of 26
saludintensiva
Sep 10, 2025 · 6 min read
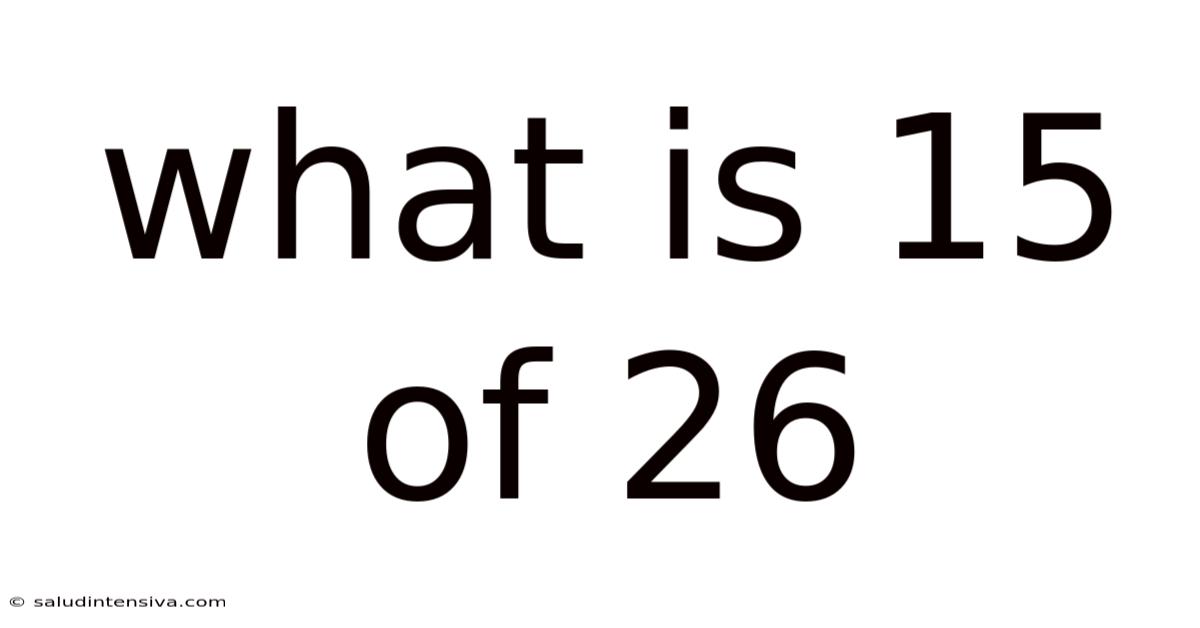
Table of Contents
What is 15 of 26? Deconstructing Fractions, Percentages, and Ratios
This article will delve into the multifaceted meaning of "15 of 26," exploring its representation as a fraction, a percentage, and a ratio. We'll examine how to calculate its value, its practical applications, and how to understand its significance within a broader mathematical context. Understanding this seemingly simple concept opens doors to more complex mathematical operations and problem-solving.
Introduction: Understanding the Fundamentals
At its core, "15 of 26" signifies a part-to-whole relationship. It describes a portion (15) out of a total (26). This can be expressed in several ways, each offering a unique perspective on the relationship between these two numbers. We'll explore these different representations and their respective uses. The key to understanding this is grasping the concepts of fractions, percentages, and ratios.
1. Representing "15 of 26" as a Fraction
The most straightforward representation of "15 of 26" is as a fraction: 15/26. A fraction is a way of expressing a part of a whole. The numerator (top number, 15) represents the part, while the denominator (bottom number, 26) represents the whole. This fraction is in its simplest form because 15 and 26 share no common factors other than 1. This means we cannot simplify it further.
Understanding Fraction Simplification: To simplify a fraction, you find the greatest common divisor (GCD) of the numerator and denominator and divide both by that number. For example, if we had the fraction 10/20, the GCD is 10. Dividing both the numerator and denominator by 10 gives us the simplified fraction 1/2. Since 15 and 26 have no common divisors other than 1, 15/26 is already in its simplest form.
2. Converting "15 of 26" to a Percentage
To express "15 of 26" as a percentage, we need to convert the fraction 15/26 into a decimal and then multiply by 100.
-
Step 1: Convert the fraction to a decimal: Divide the numerator (15) by the denominator (26): 15 ÷ 26 ≈ 0.5769
-
Step 2: Multiply by 100 to express as a percentage: 0.5769 × 100 ≈ 57.69%
Therefore, 15 out of 26 is approximately 57.69%. The percentage representation provides a readily understandable measure of the proportion. It's often used to represent proportions in contexts where comparisons are easily made. For example, if 15 out of 26 students passed an exam, we could say that approximately 57.69% of the students passed.
Understanding Percentage Calculations: Percentages are a fundamental part of many daily calculations. From calculating discounts and tax to understanding financial reports and statistics, percentages offer a standardized way of expressing proportions. Mastering percentage calculations is vital for various aspects of life.
3. Representing "15 of 26" as a Ratio
A ratio is a comparison of two or more quantities. "15 of 26" can be expressed as the ratio 15:26. This ratio reads as "15 to 26" and indicates the relative sizes of the two quantities. Ratios, like fractions, can be simplified if the numbers share common factors. However, as previously stated, 15 and 26 have no common factors other than 1, so the ratio 15:26 is already in its simplest form.
Understanding Ratio Simplification and Applications: Ratio simplification follows the same principle as fraction simplification – finding the greatest common divisor and dividing both parts of the ratio by it. Ratios are extensively used in various fields, including cooking (mixing ingredients), map scales, and comparing different quantities. For example, a map scale of 1:100,000 means that 1 unit on the map represents 100,000 units in reality.
4. Practical Applications of Understanding "15 of 26"
Understanding the different representations of "15 of 26" – as a fraction, percentage, and ratio – allows us to apply this knowledge in various practical scenarios.
-
Statistics and Probability: In statistical analysis, this concept is crucial for calculating probabilities and proportions. For instance, if you have a bag containing 26 marbles, 15 of which are red, the probability of picking a red marble is 15/26, or approximately 57.69%.
-
Surveys and Data Analysis: Survey results are often presented as percentages. If a survey of 26 people shows that 15 prefer a particular product, the result can be expressed as approximately 57.69% preference.
-
Financial Calculations: Financial calculations frequently involve proportions and percentages. For example, determining the portion of a budget allocated to specific expenses uses similar calculations.
-
Everyday Life: Many everyday situations involve proportional reasoning. Sharing items, dividing tasks, or calculating discounts all rely on the principles demonstrated in understanding "15 of 26."
5. Extending the Concept: Working with Larger Numbers and More Complex Problems
While "15 of 26" is a relatively simple example, the underlying principles can be applied to more complex scenarios. Imagine you have a larger sample size, such as 260 items with 150 possessing a specific characteristic. The calculations would remain the same: the fraction would be 150/260, which simplifies to 15/26 (by dividing both numerator and denominator by 10). The percentage and ratio would also be calculated using the same methods.
Consider a scenario involving multiple proportions. Suppose you have 260 items, 150 are red, 70 are blue, and 40 are green. You could calculate the percentage of each color:
- Red: (150/260) * 100 ≈ 57.69%
- Blue: (70/260) * 100 ≈ 26.92%
- Green: (40/260) * 100 ≈ 15.38%
This demonstrates how the understanding of basic proportions, as exemplified by "15 of 26," can be scaled to analyze more complex datasets and solve more challenging problems.
6. Frequently Asked Questions (FAQ)
Q1: What is the simplest form of the fraction 15/26?
A1: 15/26 is already in its simplest form because 15 and 26 share no common factors other than 1.
Q2: How do I convert a fraction to a percentage?
A2: Divide the numerator by the denominator and then multiply the result by 100.
Q3: Can a ratio be expressed as a fraction?
A3: Yes, a ratio can be directly expressed as a fraction. For example, the ratio 15:26 is equivalent to the fraction 15/26.
Q4: Are there any online tools to help with these calculations?
A4: Yes, many online calculators can perform fraction, percentage, and ratio calculations. However, understanding the underlying principles is crucial for problem-solving.
Q5: What if the numbers were larger and harder to calculate manually?
A5: For larger numbers, a calculator is recommended. However, the underlying principles remain the same – understanding the relationship between the numerator, denominator, and the resulting decimal and percentage.
7. Conclusion: Mastering the Fundamentals
Understanding "15 of 26" isn't just about calculating a fraction, percentage, or ratio. It's about grasping the fundamental concepts of proportions and their applications in various fields. Mastering these core concepts forms a solid foundation for more advanced mathematical studies and problem-solving skills across diverse disciplines. The ability to interpret and manipulate these mathematical concepts is valuable for navigating everyday life and succeeding in academic and professional pursuits. By understanding the relationship between fractions, percentages, and ratios, you’ve taken a significant step towards developing a stronger mathematical intuition and a more comprehensive understanding of the world around you.
Latest Posts
Latest Posts
-
Gcd Of 3 And 5
Sep 10, 2025
-
2 8 As A Decimal
Sep 10, 2025
-
How To Figure Square Inch
Sep 10, 2025
-
Gcf For 18 And 45
Sep 10, 2025
-
6 13 As A Percentage
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.