Gcd Of 3 And 5
saludintensiva
Sep 10, 2025 · 6 min read
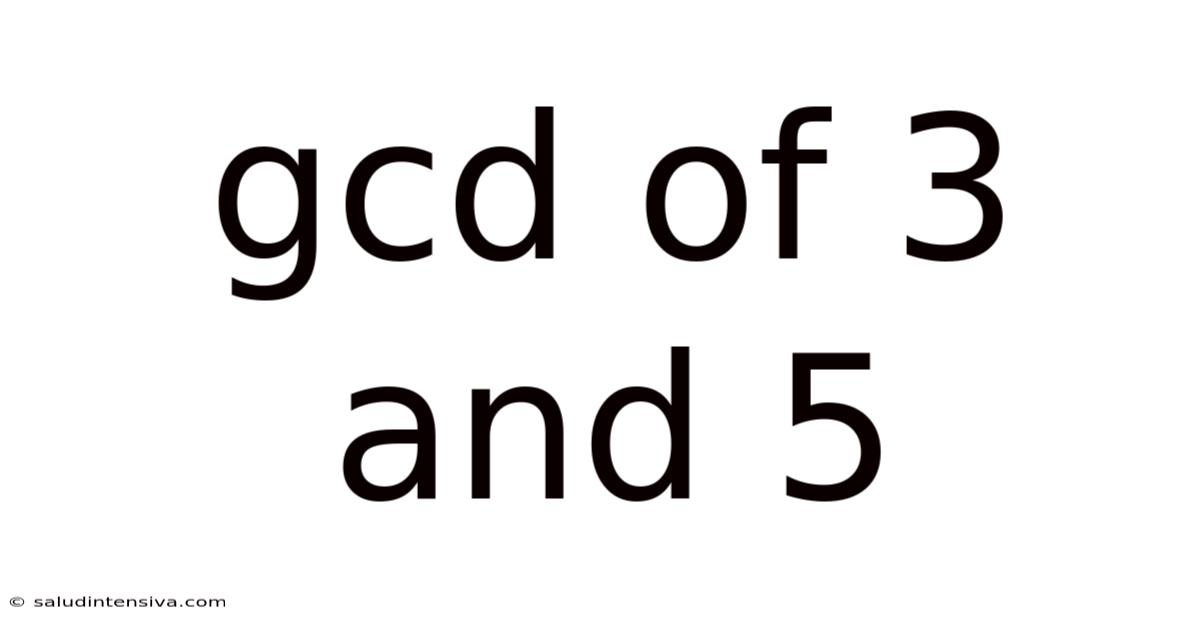
Table of Contents
Unveiling the Greatest Common Divisor: A Deep Dive into gcd(3, 5)
Finding the greatest common divisor (GCD) of two numbers might seem like a simple arithmetic task, especially when dealing with small numbers like 3 and 5. However, understanding the underlying principles behind GCD calculation opens doors to more complex mathematical concepts and applications in various fields, from cryptography to computer science. This article will embark on a comprehensive exploration of the GCD of 3 and 5, delving into different methods of calculation, the theoretical underpinnings, and its broader significance in mathematics.
Introduction to Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the greatest common factor (GCF) or highest common factor (HCF), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the GCD of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Calculating gcd(3, 5): The Easiest Case
Calculating the GCD of 3 and 5 is remarkably straightforward. Let's list the divisors of each number:
- Divisors of 3: 1, 3
- Divisors of 5: 1, 5
The only common divisor of 3 and 5 is 1. Therefore, the greatest common divisor of 3 and 5 is 1. We write this as gcd(3, 5) = 1.
Methods for Finding the GCD: Beyond Simple Inspection
While simple inspection works well for small numbers like 3 and 5, more sophisticated methods are necessary for larger numbers. Let's explore some common techniques:
1. Prime Factorization Method
This method involves finding the prime factorization of each number and identifying the common prime factors raised to the lowest power.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
Since 3 and 5 have no common prime factors, their GCD is 1.
2. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCD of two integers. It's based on the principle that the GCD of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's apply the Euclidean algorithm to 3 and 5:
- Step 1: Since 5 > 3, we subtract 3 from 5: 5 - 3 = 2. Now we find the GCD of 3 and 2.
- Step 2: Now we have 3 > 2. Subtract 2 from 3: 3 - 2 = 1. Now we find the GCD of 2 and 1.
- Step 3: 2 > 1. Subtract 1 from 2: 2 - 1 = 1. Now we find the GCD of 1 and 1.
- Step 4: The numbers are equal (1 and 1). Therefore, the GCD is 1.
The Euclidean algorithm provides a systematic and efficient way to compute the GCD, especially for larger numbers where prime factorization might be computationally intensive.
3. Listing Common Divisors
This method is suitable for smaller numbers. You list all the divisors of each number and then identify the largest number that appears in both lists. As we saw earlier, the only common divisor of 3 and 5 is 1.
Mathematical Properties of GCD
The GCD possesses several important mathematical properties:
- Commutativity: gcd(a, b) = gcd(b, a). The order of the numbers doesn't matter.
- Associativity: gcd(a, gcd(b, c)) = gcd(gcd(a, b), c). This allows us to extend the GCD to more than two numbers.
- Distributivity with Multiplication: gcd(am, bm) = m * gcd(a, b). If we multiply both numbers by the same factor, the GCD is also multiplied by that factor.
- GCD and LCM: The product of the GCD and the least common multiple (LCM) of two numbers is equal to the product of the two numbers: gcd(a, b) * lcm(a, b) = a * b.
Understanding these properties is crucial for solving more advanced mathematical problems involving GCDs.
Applications of GCD
The GCD has far-reaching applications in various fields:
- Cryptography: The GCD plays a fundamental role in public-key cryptography algorithms, such as RSA, which relies on the difficulty of finding the GCD of two very large numbers.
- Computer Science: The GCD is used in algorithms for simplifying fractions, finding least common multiples, and solving Diophantine equations.
- Music Theory: The GCD is used to determine the greatest common divisor of the frequencies of two notes, which helps in understanding musical intervals and harmony.
- Geometry: GCD is used to solve problems related to finding the greatest common measure of lengths.
Relatively Prime Numbers: The Case of 3 and 5
Two numbers are considered relatively prime or coprime if their GCD is 1. Since gcd(3, 5) = 1, 3 and 5 are relatively prime. This means they share no common factors other than 1. This concept is crucial in number theory and has implications in various applications, including cryptography.
Extending the Concept: GCD of More Than Two Numbers
The concept of GCD can be extended to more than two numbers. For example, to find the GCD of 3, 5, and 10, we can use the Euclidean algorithm iteratively or the prime factorization method:
- Prime Factorization Method:
- 3 = 3
- 5 = 5
- 10 = 2 * 5
There are no common prime factors among 3, 5, and 10. Therefore, gcd(3, 5, 10) = 1.
- Euclidean Algorithm (iterative): We can first find the GCD of 3 and 5 (which is 1), and then find the GCD of that result (1) and 10, which is still 1.
Frequently Asked Questions (FAQ)
Q1: What is the significance of a GCD of 1?
A1: A GCD of 1 indicates that the two numbers are relatively prime or coprime, meaning they share no common factors other than 1. This property is crucial in various mathematical and computational applications.
Q2: Can the GCD of two numbers be larger than the smaller number?
A2: No, the GCD of two numbers can never be larger than the smaller of the two numbers. The GCD is, by definition, a divisor of both numbers.
Q3: Is there a limit to the size of numbers for which the Euclidean algorithm can find the GCD?
A3: Theoretically, the Euclidean algorithm can find the GCD of any two integers, regardless of their size. However, the computational time increases with the size of the numbers.
Q4: How is the GCD related to the LCM?
A4: The GCD and LCM of two numbers are inversely related. Their product is equal to the product of the two numbers: gcd(a, b) * lcm(a, b) = a * b.
Conclusion: Beyond the Simple Calculation
While finding the GCD of 3 and 5 might seem trivial, it serves as a foundational stepping stone to a deeper understanding of number theory, algorithms, and their practical applications. The seemingly simple calculation of gcd(3, 5) = 1 unveils the rich tapestry of mathematical relationships and its far-reaching impact across various disciplines. Mastering the concepts of GCD, the various methods for its calculation, and its properties is crucial for anyone interested in pursuing advanced studies in mathematics and computer science. The simplicity of this specific example belies the power and importance of this fundamental concept in mathematics.
Latest Posts
Latest Posts
-
What Is 2 3 Of 5
Sep 11, 2025
-
300 000 Minutes To Hours
Sep 11, 2025
-
3 1 2 1 2
Sep 11, 2025
-
Gcf Of 32 And 36
Sep 11, 2025
-
Km Per Gallon To Mpg
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Gcd Of 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.