Factor X 2 4x 6
saludintensiva
Sep 21, 2025 · 6 min read
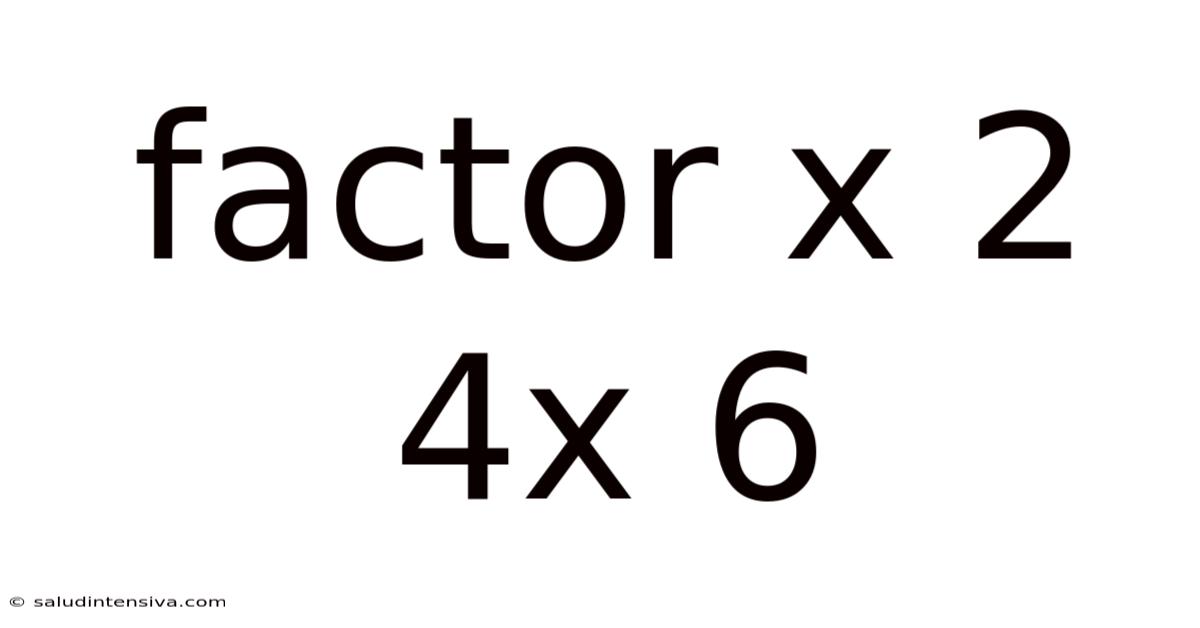
Table of Contents
Unveiling the Mysteries of Factoring: A Deep Dive into x² + 4x + 6
Many students encounter quadratic expressions like x² + 4x + 6 and find themselves stumped. Factoring, the process of breaking down a polynomial into simpler expressions, is a fundamental skill in algebra. While some quadratics factor neatly into (x + a)(x + b), others, like our example, present a greater challenge. This article will explore the nuances of factoring x² + 4x + 6, delving into the methods used, the reasons behind the complexities, and provide a broader understanding of quadratic expressions. We'll tackle the problem head-on, explain why simple factoring fails, and introduce alternative approaches to manipulate and solve equations involving this specific expression.
Understanding Quadratic Expressions
Before we dissect x² + 4x + 6, let's establish a solid foundation. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form is ax² + bx + c, where 'a', 'b', and 'c' are constants. Factoring aims to rewrite this expression as a product of two simpler expressions, often linear binomials. This is incredibly useful for solving quadratic equations (where the expression equals zero), finding roots, and simplifying more complex algebraic manipulations.
Simple Factoring: The simplest form of factoring involves finding two numbers that add up to 'b' and multiply to 'ac'. For example, in the expression x² + 5x + 6, we look for two numbers that add to 5 and multiply to 6 (3 and 2). This allows us to factor it as (x + 3)(x + 2).
Why x² + 4x + 6 Doesn't Factor Simply
The beauty and challenge of algebra lie in its exceptions. While many quadratic expressions yield to simple factoring, x² + 4x + 6 presents a different scenario. Let's try to find two numbers that add up to 4 and multiply to 6. The pairs of factors of 6 are (1, 6), (2, 3), (-1, -6), and (-2, -3). None of these pairs add up to 4. This indicates that x² + 4x + 6 cannot be factored using simple integer coefficients.
This doesn't mean the expression is unworkable. It simply means we need to employ more advanced techniques.
Alternative Approaches: Beyond Simple Factoring
When simple factoring fails, several other avenues can be explored:
1. Completing the Square: This method transforms the quadratic expression into a perfect square trinomial, plus a constant. A perfect square trinomial is an expression that can be factored into the square of a binomial (e.g., (x + a)²).
Let's complete the square for x² + 4x + 6:
-
Step 1: Focus on the x² and 4x terms. We need to find a number that, when added and subtracted, completes the square. Take half of the coefficient of x (which is 4), square it (2² = 4), and add and subtract it: x² + 4x + 4 - 4 + 6
-
Step 2: Rewrite the expression: (x² + 4x + 4) + 2
-
Step 3: Factor the perfect square trinomial: (x + 2)² + 2
This form is valuable for various applications, including finding the vertex of a parabola representing the quadratic function.
2. Quadratic Formula: This is a powerful tool for finding the roots (or zeros) of any quadratic equation, even those that are not easily factorable. The quadratic formula is derived from completing the square and is expressed as:
x = [-b ± √(b² - 4ac)] / 2a
For our expression x² + 4x + 6 = 0 (setting it equal to zero to find the roots), a = 1, b = 4, and c = 6. Plugging these values into the quadratic formula gives:
x = [-4 ± √(4² - 4 * 1 * 6)] / 2 * 1 x = [-4 ± √(16 - 24)] / 2 x = [-4 ± √(-8)] / 2 x = [-4 ± 2i√2] / 2 x = -2 ± i√2
The presence of the imaginary unit 'i' (where i² = -1) indicates that the roots are complex numbers. This reinforces the fact that the quadratic expression doesn't factor neatly into real-number binomials.
3. Graphing the Quadratic: Visualizing the quadratic function y = x² + 4x + 6 can provide valuable insights. The parabola will not intersect the x-axis, confirming that there are no real roots, which aligns with our findings using the quadratic formula. The absence of real roots further explains the difficulty in finding simple real number factors.
The Significance of Complex Roots
The fact that x² + 4x + 6 has complex roots is not a mathematical anomaly; it's a fundamental characteristic of certain quadratic expressions. Complex numbers extend the realm of algebra beyond real numbers, allowing us to solve equations that previously had no solutions within the real number system. Complex numbers are essential in various fields like electrical engineering, quantum mechanics, and signal processing.
Applications and Further Exploration
The inability to factor x² + 4x + 6 using simple methods highlights the importance of understanding diverse algebraic techniques. These methods extend beyond simply finding factors; they provide a deeper understanding of the nature of quadratic equations and their solutions. The expression itself might appear in various contexts:
- Calculus: Finding derivatives and integrals often involves manipulating quadratic expressions.
- Physics: Quadratic equations frequently model projectile motion, oscillations, and other physical phenomena.
- Engineering: Design and analysis in various engineering disciplines rely heavily on solving quadratic equations.
Frequently Asked Questions (FAQs)
-
Q: Can all quadratic expressions be factored?
- A: No. While many can be factored using integers, some, like x² + 4x + 6, require more advanced techniques or have complex roots, preventing simple factorization with real numbers.
-
Q: What if I need to solve an equation containing x² + 4x + 6?
- A: Use the quadratic formula or complete the square to find the roots (solutions) of the equation.
-
Q: Is there a quick way to determine if a quadratic expression is easily factorable?
- A: Examining the discriminant (b² - 4ac) from the quadratic formula helps. If the discriminant is a perfect square and positive, the expression factors nicely with real numbers. If it's negative, the roots are complex. If it's zero, there's one repeated real root.
-
Q: Why is understanding complex numbers important?
- A: Complex numbers are crucial for solving certain types of equations and for representing various phenomena in various fields of science and engineering. They expand the scope of mathematical possibilities.
Conclusion
Factoring x² + 4x + 6 directly using simple integer factors isn't possible. However, this seemingly intractable problem reveals the richness and depth of algebra. By employing methods like completing the square and the quadratic formula, we can fully analyze the expression, uncover its complex roots, and appreciate the broader mathematical landscape it represents. The inability to factor this expression simply underscores the importance of mastering a range of algebraic techniques to tackle various mathematical challenges effectively. The journey to understand this seemingly simple problem opens the door to a more profound understanding of quadratic equations and their applications in diverse fields.
Latest Posts
Latest Posts
-
What Was 100 Days Ago
Sep 21, 2025
-
85 Percent As A Decimal
Sep 21, 2025
-
Acceleration Of Gravity In Feet
Sep 21, 2025
-
Graph Of X 2 9
Sep 21, 2025
-
90 Days From September 6
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 4x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.