Factor X 2 5x 4
saludintensiva
Sep 20, 2025 · 7 min read
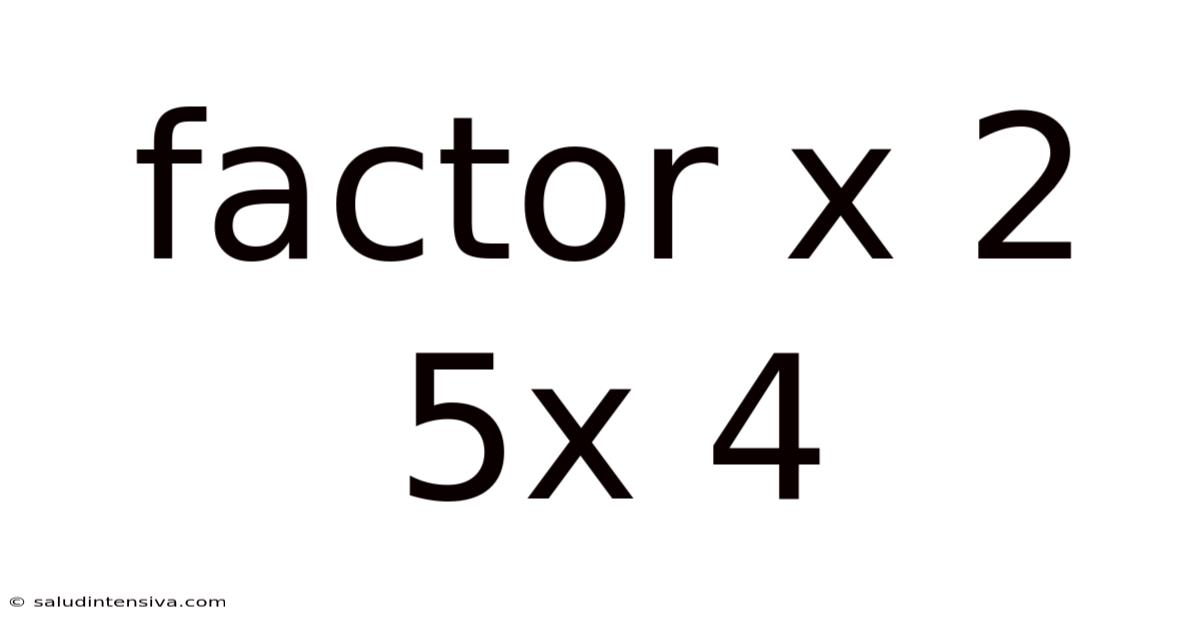
Table of Contents
Unraveling the Mystery: A Deep Dive into the Quadratic Expression x² + 5x + 4
The seemingly simple quadratic expression, x² + 5x + 4, hides a wealth of mathematical concepts within its concise form. Understanding this expression unlocks a gateway to comprehending factoring, solving quadratic equations, graphing parabolas, and appreciating the elegance of algebraic manipulation. This article will explore this expression in detail, from its basic factorization to its graphical representation and practical applications. We'll uncover its secrets step-by-step, making it accessible even to those with a limited mathematical background.
Understanding Quadratic Expressions
Before diving into the specifics of x² + 5x + 4, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants (numbers), and a is not equal to zero. In our case, a = 1, b = 5, and c = 4.
The significance of quadratic expressions lies in their widespread applications across various fields, including physics (projectile motion), engineering (structural design), economics (modeling supply and demand), and computer science (algorithm optimization). Understanding how to manipulate and solve these expressions is crucial for success in these areas.
Factoring the Expression: x² + 5x + 4
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions. This process is essential for solving quadratic equations and simplifying more complex algebraic expressions. The goal is to find two binomials (expressions with two terms) whose product equals the original quadratic.
For x² + 5x + 4, we look for two numbers that add up to 5 (the coefficient of x) and multiply to 4 (the constant term). These numbers are 1 and 4. Therefore, the factored form of x² + 5x + 4 is (x + 1)(x + 4).
Let's verify this:
(x + 1)(x + 4) = x(x + 4) + 1(x + 4) = x² + 4x + x + 4 = x² + 5x + 4
The factorization is correct! This simple factorization unlocks a deeper understanding of the expression's behavior and properties.
Solving the Quadratic Equation: x² + 5x + 4 = 0
Once we've factored the quadratic expression, we can use it to solve the corresponding quadratic equation: x² + 5x + 4 = 0. The solutions to this equation are the values of x that make the equation true. Since the expression is already factored, we can use the zero-product property: if the product of two factors is zero, then at least one of the factors must be zero.
Therefore, we set each factor equal to zero and solve for x:
x + 1 = 0 => x = -1 x + 4 = 0 => x = -4
The solutions to the equation x² + 5x + 4 = 0 are x = -1 and x = -4. These are also known as the roots or zeros of the quadratic equation. These values represent the x-intercepts of the parabola that represents the quadratic function y = x² + 5x + 4.
Graphing the Parabola: y = x² + 5x + 4
The quadratic expression can be represented graphically as a parabola. The parabola's shape is determined by the coefficient of x² (a). Since a = 1 (positive), the parabola opens upwards. The vertex (the lowest point of the parabola) can be found using the formula x = -b/2a. In this case, x = -5/(2*1) = -2.5. Substituting this value back into the equation, we find the y-coordinate of the vertex: y = (-2.5)² + 5(-2.5) + 4 = -2.25. So the vertex is at (-2.5, -2.25).
The x-intercepts are the points where the parabola crosses the x-axis. These are the solutions we found earlier: (-1, 0) and (-4, 0). The y-intercept is the point where the parabola crosses the y-axis, which occurs when x = 0. Substituting x = 0 into the equation gives y = 4. So the y-intercept is (0, 4).
By plotting these points and sketching a smooth curve through them, we obtain the graph of the parabola y = x² + 5x + 4. This visual representation provides further insight into the behavior of the quadratic expression. It shows the range of values the expression can take, its minimum value (at the vertex), and the values of x for which the expression equals zero (the x-intercepts).
The Discriminant and Nature of Roots
The discriminant of a quadratic equation ax² + bx + c = 0 is given by the expression b² - 4ac. The discriminant helps determine the nature of the roots (solutions) of the quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots. This means the parabola intersects the x-axis at two different points.
- b² - 4ac = 0: The equation has one real root (a repeated root). The parabola touches the x-axis at exactly one point (the vertex).
- b² - 4ac < 0: The equation has no real roots. The parabola does not intersect the x-axis.
For our equation, x² + 5x + 4 = 0, the discriminant is 5² - 4(1)(4) = 25 - 16 = 9. Since the discriminant is positive, the equation has two distinct real roots, which we've already found to be -1 and -4.
Applications of Quadratic Expressions
Quadratic expressions are fundamental building blocks in numerous mathematical and real-world applications. Here are a few examples:
- Projectile Motion: The trajectory of a projectile (e.g., a ball thrown in the air) can be modeled using a quadratic equation. The equation describes the height of the projectile as a function of time.
- Area Calculations: Finding the area of certain geometric shapes, such as rectangles with variable dimensions, involves quadratic expressions.
- Optimization Problems: Quadratic equations are used in optimization problems to find maximum or minimum values of a function. For instance, finding the maximum profit given a certain production cost.
- Physics and Engineering: Many physical phenomena, such as the motion of a spring or the deflection of a beam, can be described using quadratic equations.
Further Exploration: Completing the Square
Another method for solving quadratic equations is completing the square. This technique involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
To complete the square for x² + 5x + 4 = 0, we follow these steps:
- Move the constant term to the right side of the equation: x² + 5x = -4
- Take half of the coefficient of x (5/2), square it (25/4), and add it to both sides of the equation: x² + 5x + 25/4 = -4 + 25/4
- Factor the left side as a perfect square: (x + 5/2)² = 9/4
- Take the square root of both sides: x + 5/2 = ±3/2
- Solve for x: x = -5/2 ± 3/2. This gives x = -1 and x = -4, the same solutions we obtained using factoring.
Frequently Asked Questions (FAQ)
Q: What if the coefficient of x² is not 1?
A: If the coefficient of x² is not 1, you can often factor out the greatest common factor (GCF) first, or use more advanced techniques like the quadratic formula.
Q: What is the quadratic formula?
A: The quadratic formula is a general method for solving quadratic equations of the form ax² + bx + c = 0. The formula is: x = (-b ± √(b² - 4ac)) / 2a.
Q: Can all quadratic expressions be factored easily?
A: No, some quadratic expressions cannot be easily factored using integer coefficients. In such cases, the quadratic formula or completing the square are more appropriate methods.
Conclusion
The seemingly simple quadratic expression x² + 5x + 4 offers a rich tapestry of mathematical concepts. From its factorization and the resulting solutions to its graphical representation as a parabola and its numerous real-world applications, this expression provides a solid foundation for understanding more advanced algebraic concepts. This exploration should not only equip you with the skills to manipulate and solve this specific expression but also build a more robust understanding of quadratic equations in general. Remember to practice these techniques to build confidence and mastery in this crucial area of algebra. The journey into deeper mathematical understanding starts with these seemingly small, yet powerfully fundamental building blocks.
Latest Posts
Latest Posts
-
3 3 5 Improper Fraction
Sep 20, 2025
-
Is 6 8 Equal To 9 12
Sep 20, 2025
-
320 Min T O Hours
Sep 20, 2025
-
11 3 As A Mixed Number
Sep 20, 2025
-
Average Internship Pay Per Hour
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 5x 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.