Gcd Of 10 And 20
saludintensiva
Sep 18, 2025 · 6 min read
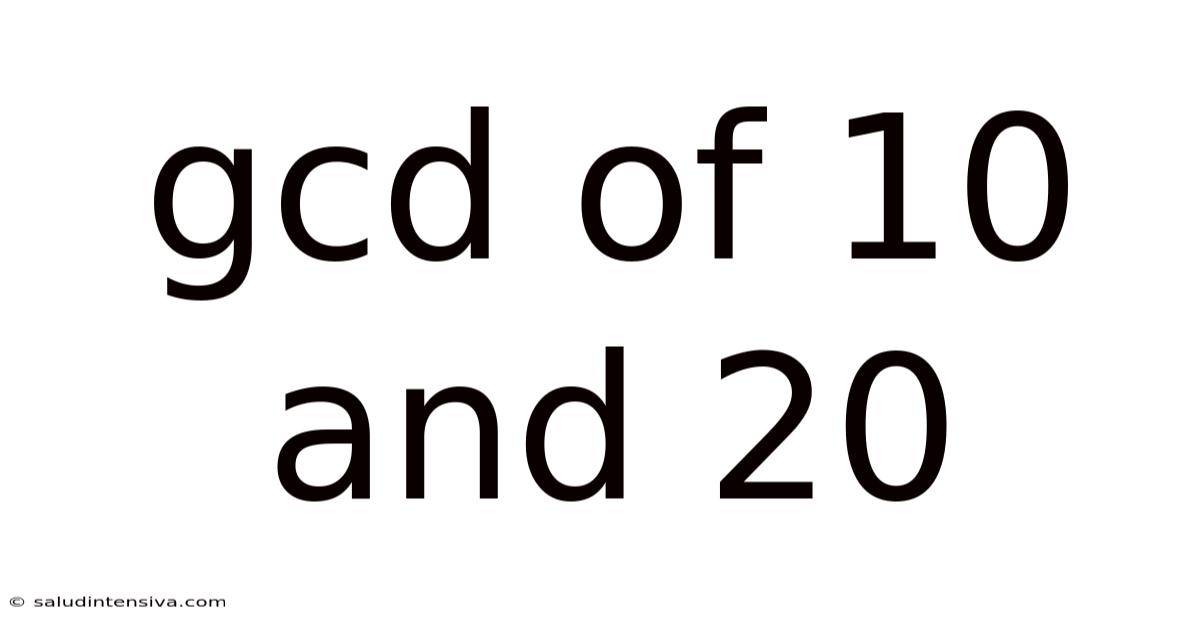
Table of Contents
Unveiling the Greatest Common Divisor: A Deep Dive into gcd(10, 20)
Finding the greatest common divisor (GCD) of two numbers might seem like a simple arithmetic task, especially when dealing with smaller numbers like 10 and 20. However, understanding the underlying principles and exploring different methods for calculating the GCD provides a valuable foundation in number theory and algorithm design. This article will delve into the GCD of 10 and 20, exploring various approaches, explaining the underlying mathematical concepts, and extending the discussion to encompass more complex scenarios. We'll also address frequently asked questions and solidify our understanding with practical examples.
Understanding the Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For instance, the divisors of 10 are 1, 2, 5, and 10, while the divisors of 20 are 1, 2, 4, 5, 10, and 20. The common divisors of 10 and 20 are 1, 2, 5, and 10. The largest among these is 10, making 10 the GCD of 10 and 20. We write this as gcd(10, 20) = 10.
Method 1: Listing the Divisors
The most straightforward method, particularly suitable for smaller numbers, is to list all the divisors of each number and identify the largest common divisor.
Steps:
- Find the divisors of 10: 1, 2, 5, 10
- Find the divisors of 20: 1, 2, 4, 5, 10, 20
- Identify the common divisors: 1, 2, 5, 10
- Determine the greatest common divisor: 10
This method is intuitive but becomes cumbersome for larger numbers as the number of divisors increases significantly.
Method 2: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Steps:
- Find the prime factorization of 10: 2 × 5
- Find the prime factorization of 20: 2² × 5
- Identify common prime factors: 2 and 5
- Raise each common prime factor to the lowest power it appears in the factorizations: 2¹ and 5¹
- Multiply the resulting terms: 2 × 5 = 10
Therefore, the GCD(10, 20) = 10. This method is more efficient than listing divisors for larger numbers, but still can be computationally intensive for extremely large numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCD of two integers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCD. A more efficient version uses the modulo operator (%) which finds the remainder after division.
Steps (using the modulo operator):
- Divide the larger number (20) by the smaller number (10): 20 ÷ 10 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number: 10
The Euclidean algorithm can be expressed recursively:
gcd(a, b) = gcd(b, a % b) where a % b is the remainder when a is divided by b.
Let's illustrate this for slightly larger numbers: Find gcd(48, 18)
- gcd(48, 18) = gcd(18, 48 % 18) = gcd(18, 12)
- gcd(18, 12) = gcd(12, 18 % 12) = gcd(12, 6)
- gcd(12, 6) = gcd(6, 12 % 6) = gcd(6, 0)
- Since the remainder is 0, the GCD is 6.
This recursive approach significantly reduces the computational complexity compared to the previous methods, making it highly suitable for large numbers.
Extending the Concept: GCD and Linear Combinations
A fascinating property of the GCD is its connection to linear combinations. Bézout's identity states that for any two integers a and b, there exist integers x and y such that:
ax + by = gcd(a, b)
For our example, gcd(10, 20) = 10. We can find integers x and y that satisfy the equation:
10x + 20y = 10
One solution is x = 1 and y = 0. (10 * 1 + 20 * 0 = 10) Other solutions exist, demonstrating the flexibility of this relationship. Finding these x and y often involves the extended Euclidean algorithm, a variation of the basic Euclidean algorithm.
Applications of the GCD
The concept of the greatest common divisor has numerous applications across various fields:
-
Fraction Simplification: The GCD is crucial for simplifying fractions to their lowest terms. For example, the fraction 20/10 simplifies to 2/1 (or simply 2) because gcd(20, 10) = 10.
-
Cryptography: GCD plays a vital role in public-key cryptography algorithms like RSA, where finding the GCD of two large numbers is essential for key generation and decryption.
-
Computer Science: The Euclidean algorithm and its variations are fundamental in computer science algorithms related to modular arithmetic, polynomial division, and other number-theoretic computations.
-
Music Theory: GCD can be used to determine the greatest common divisor of two musical intervals, helping to understand harmonic relationships.
-
Geometry: GCD finds application in solving geometric problems related to finding common measures in shapes and patterns.
Frequently Asked Questions (FAQ)
Q1: What is the GCD of two prime numbers?
A1: The GCD of two distinct prime numbers is always 1 because prime numbers are only divisible by 1 and themselves.
Q2: What if one of the numbers is 0?
A2: The GCD of any integer and 0 is the absolute value of that integer. For example, gcd(10, 0) = 10.
Q3: Can the Euclidean algorithm be used for more than two numbers?
A3: Yes, you can extend the Euclidean algorithm to find the GCD of multiple numbers. You would repeatedly apply the algorithm, starting with the first two numbers, then finding the GCD of the result and the next number, and so on. For example, to find gcd(10, 20, 30), you'd first find gcd(10, 20) = 10, then find gcd(10, 30) = 10.
Q4: Are there any limitations to the Euclidean algorithm?
A4: The Euclidean algorithm is remarkably efficient for finding the GCD of integers. However, its direct application to very large numbers might still be computationally expensive, though optimized versions exist to mitigate this. Also, the algorithm is specific to integers and does not directly apply to non-integer numbers or more complex algebraic structures.
Conclusion
Understanding the greatest common divisor is crucial for various mathematical and computational tasks. While simple methods like listing divisors are suitable for smaller numbers, the Euclidean algorithm stands out as a remarkably efficient and elegant method for calculating the GCD of larger integers. Its application extends beyond basic arithmetic, influencing numerous fields from cryptography to music theory. By mastering the different methods and understanding the underlying principles, you gain a powerful tool for tackling a wide array of mathematical challenges. The seemingly simple problem of finding gcd(10, 20) = 10 serves as a gateway to a deeper understanding of number theory and its applications in the broader world.
Latest Posts
Latest Posts
-
Random Number Generator 0 99
Sep 18, 2025
-
60 Days From 1 15
Sep 18, 2025
-
First 6 Multiples Of 5
Sep 18, 2025
-
5 1 4 2 3 4
Sep 18, 2025
-
When Was 29 Weeks Ago
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcd Of 10 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.