Gcd Of 2 And 4
saludintensiva
Sep 17, 2025 · 6 min read
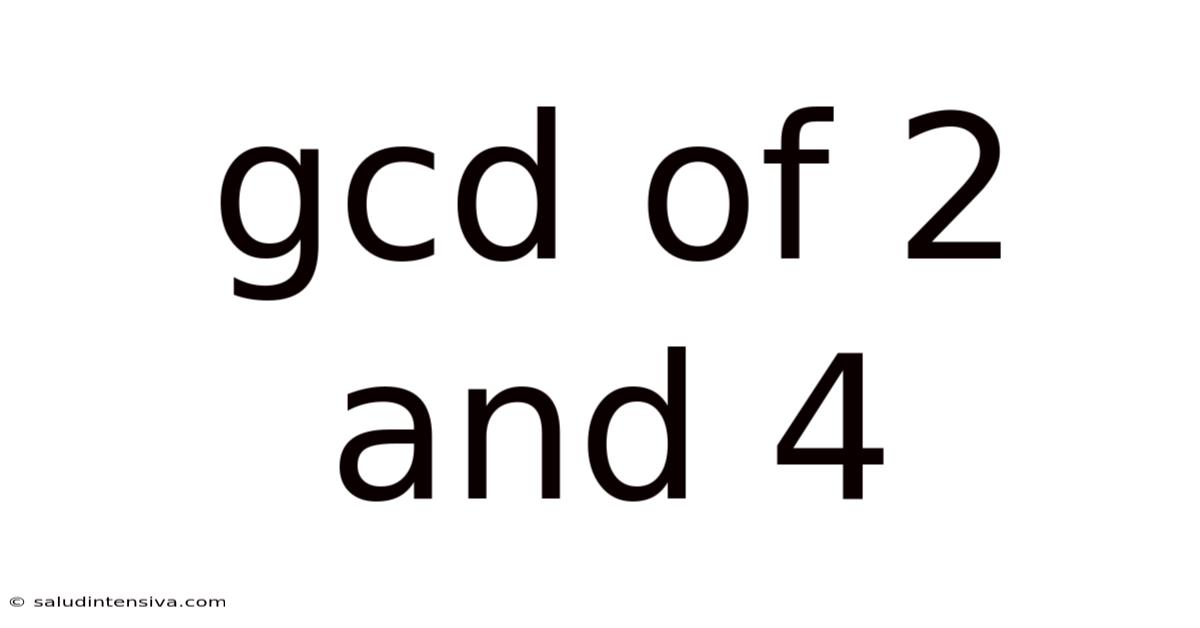
Table of Contents
Unveiling the Greatest Common Divisor: A Deep Dive into gcd(2, 4)
Finding the greatest common divisor (GCD) of two numbers might seem like a trivial task, especially when dealing with small numbers like 2 and 4. However, understanding the concept of GCD and the various methods to calculate it forms the foundation of many advanced mathematical concepts in number theory, cryptography, and computer science. This article will explore the GCD of 2 and 4 in detail, not just providing the answer but also delving into the underlying principles, different calculation methods, and its broader significance in mathematics.
Introduction: What is a Greatest Common Divisor?
The greatest common divisor (GCD), also known as the highest common factor (HCF), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the divisors of 12 are 1, 2, 3, 4, 6, and 12. The divisors of 18 are 1, 2, 3, 6, 9, and 18. The common divisors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common divisors is 6, therefore, the GCD(12, 18) = 6.
Understanding the GCD is crucial in various mathematical operations, including simplifying fractions, solving Diophantine equations, and in more advanced areas like abstract algebra and cryptography. This seemingly simple concept lays the groundwork for much more complex mathematical theories.
Calculating the GCD(2, 4): Simple Observation
Let's start with the simplest approach for finding the GCD of 2 and 4. By listing the divisors of each number, we can easily identify the greatest common divisor.
- Divisors of 2: 1, 2
- Divisors of 4: 1, 2, 4
The common divisors of 2 and 4 are 1 and 2. The greatest of these is 2. Therefore, the GCD(2, 4) = 2.
This method works well for small numbers, but becomes cumbersome and inefficient for larger numbers. Let's explore more efficient methods.
Euclidean Algorithm: A Systematic Approach
The Euclidean algorithm is a highly efficient method for calculating the GCD of two integers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's apply the Euclidean algorithm to find the GCD(2, 4):
- Start with the two numbers: 2 and 4.
- Subtract the smaller number from the larger number: 4 - 2 = 2.
- Replace the larger number with the result: Now we have 2 and 2.
- Since the numbers are equal, the GCD is 2.
The Euclidean algorithm offers a systematic and efficient way to find the GCD, particularly useful for larger numbers where listing divisors becomes impractical. It's based on the property that gcd(a, b) = gcd(a, b-a) = gcd(a, b-ka) where 'k' is any integer. This iterative subtraction can be optimized further using modulo operation.
Euclidean Algorithm using Modulo Operation:
The modulo operation (%) gives the remainder after division. The Euclidean algorithm can be expressed more efficiently using the modulo operation:
- Start with the two numbers: a and b (where b > a).
- Calculate the remainder: r = b % a.
- If r = 0, then a is the GCD.
- Otherwise, replace b with a and a with r, and repeat steps 2 and 3.
Let's apply this to GCD(2, 4):
- a = 2, b = 4
- r = 4 % 2 = 0
- Since r = 0, the GCD is a = 2.
This modulo-based version of the Euclidean algorithm is even more efficient for computational purposes, especially when dealing with very large numbers.
Prime Factorization Method:
Another method for finding the GCD involves finding the prime factorization of each number. The GCD is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 2: 2¹
- Prime factorization of 4: 2²
The only common prime factor is 2. The lowest power of 2 is 2¹. Therefore, the GCD(2, 4) = 2.
While this method is conceptually straightforward, finding the prime factorization of large numbers can be computationally expensive, making the Euclidean algorithm a more practical choice for larger numbers.
Visualizing the GCD: Geometric Interpretation
The GCD can be visualized geometrically. Imagine you have a rectangle with dimensions 2 units and 4 units. The GCD represents the size of the largest square tiles that can perfectly cover this rectangle without any gaps or overlaps. In this case, 2x2 squares would perfectly tile the 2x4 rectangle, demonstrating that the GCD(2, 4) = 2. This geometric interpretation provides an intuitive understanding of the concept.
Applications of GCD:
The seemingly simple concept of GCD has far-reaching applications across various fields:
-
Simplifying Fractions: Finding the GCD of the numerator and denominator allows you to simplify fractions to their lowest terms. For example, the fraction 4/6 can be simplified to 2/3 by dividing both numerator and denominator by their GCD, which is 2.
-
Cryptography: The GCD plays a crucial role in various cryptographic algorithms, such as the RSA algorithm, which relies on the difficulty of finding the GCD of two very large numbers.
-
Computer Science: The GCD is used in various computer science algorithms, including those related to graph theory, data structures, and scheduling.
-
Music Theory: The GCD is used to determine the greatest common divisor of the frequencies of two notes, which helps in understanding musical intervals and harmony.
Frequently Asked Questions (FAQ):
-
Q: What if the GCD of two numbers is 1?
- A: If the GCD of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the GCD of two numbers be zero?
- A: No, the GCD is always a positive integer. The GCD is only defined for positive integers.
-
Q: How do I find the GCD of more than two numbers?
- A: You can find the GCD of more than two numbers by repeatedly applying the Euclidean algorithm. Find the GCD of the first two numbers, then find the GCD of that result and the third number, and so on.
-
Q: Is there a formula for calculating the GCD?
- A: There isn't a single, simple formula for calculating the GCD for all cases. The Euclidean algorithm and prime factorization methods provide algorithmic approaches.
Conclusion: Beyond the Simple Answer
While the GCD of 2 and 4 is simply 2, this seemingly simple calculation opens a door to a vast and fascinating world of mathematical concepts and applications. Understanding the different methods for calculating the GCD, their underlying principles, and their practical uses is crucial for anyone pursuing further studies in mathematics, computer science, or related fields. The Euclidean algorithm, in particular, showcases the elegance and efficiency of mathematical techniques, highlighting how a simple concept can have profound implications in diverse areas. The exploration of GCD serves as a perfect example of how fundamental mathematical concepts form the building blocks of complex systems and advanced technologies.
Latest Posts
Latest Posts
-
Gcf Of 27 And 72
Sep 17, 2025
-
What Is 3 Times 1 2
Sep 17, 2025
-
What Time Is 15 26
Sep 17, 2025
-
Gcf Of 54 And 90
Sep 17, 2025
-
Lcm For 12 And 9
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcd Of 2 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.