Gcf Of 12 And 32
saludintensiva
Sep 15, 2025 · 7 min read
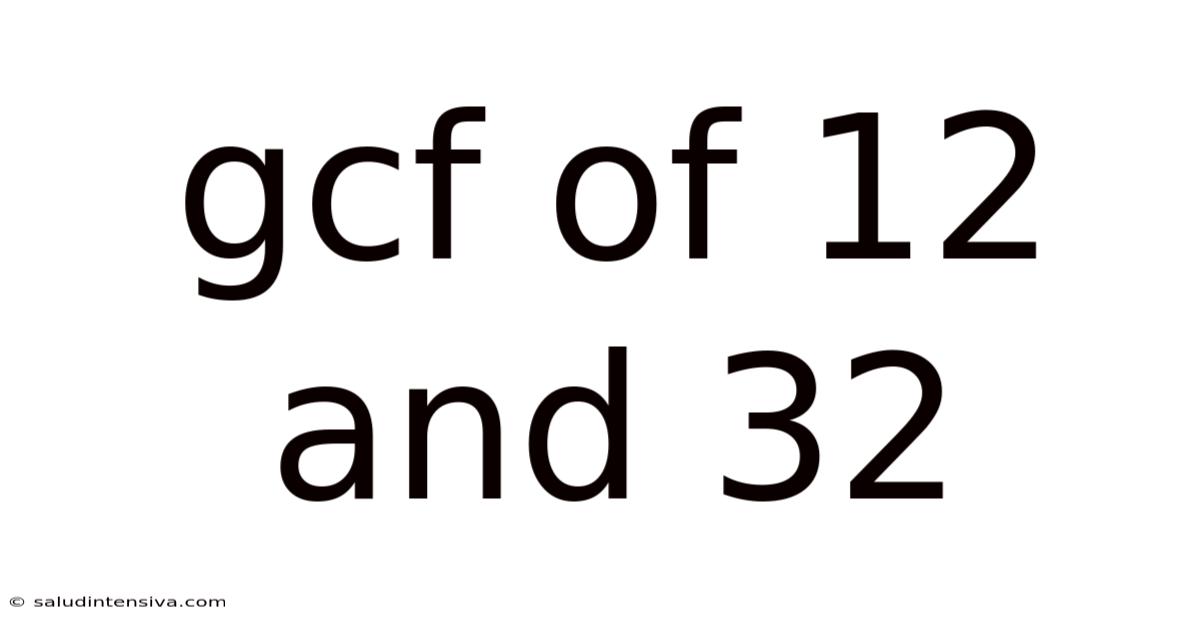
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 12 and 32: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and different methods for calculating the GCF offers a deeper understanding of number theory and its practical applications. This comprehensive guide delves into the intricacies of finding the GCF of 12 and 32, exploring various techniques and illustrating their application with clear examples. We'll move beyond a simple answer and explore the "why" behind the calculations, making this concept accessible to everyone, from elementary school students to those brushing up on their math skills.
Understanding the Concept of Greatest Common Factor (GCF)
The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 32 are 1, 2, 4, 8, 16, and 32. The common factors of 12 and 32 are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 12 and 32 is 4.
This concept is crucial in various mathematical operations, including simplifying fractions, solving algebraic equations, and even in more advanced areas like cryptography. Mastering the techniques to find the GCF lays a strong foundation for future mathematical endeavors.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 12 and 32, is to list all the factors of each number and then identify the largest common factor.
Steps:
- List the factors of 12: 1, 2, 3, 4, 6, 12
- List the factors of 32: 1, 2, 4, 8, 16, 32
- Identify the common factors: 1, 2, 4
- Determine the greatest common factor: The largest common factor is 4.
Therefore, the GCF(12, 32) = 4. This method is simple and intuitive, making it ideal for beginners. However, for larger numbers, this approach can become cumbersome and time-consuming.
Method 2: Prime Factorization
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. Prime factorization involves breaking down each number into its prime factors.
Steps:
- Find the prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Find the prime factorization of 32: 32 = 2 x 2 x 2 x 2 x 2 = 2⁵
- Identify common prime factors: Both 12 and 32 share the prime factor 2.
- Determine the lowest power of the common prime factors: The lowest power of 2 that appears in both factorizations is 2².
- Calculate the GCF: The GCF is the product of the common prime factors raised to their lowest powers. In this case, GCF(12, 32) = 2² = 4.
This method is more efficient than listing factors, especially when dealing with larger numbers. It provides a structured approach that is less prone to errors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where prime factorization becomes more complex. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
- Start with the two numbers: 12 and 32.
- Divide the larger number by the smaller number and find the remainder: 32 ÷ 12 = 2 with a remainder of 8.
- Replace the larger number with the smaller number and the smaller number with the remainder: The new pair is 12 and 8.
- Repeat the process: 12 ÷ 8 = 1 with a remainder of 4.
- Repeat again: 8 ÷ 4 = 2 with a remainder of 0.
- The GCF is the last non-zero remainder: The last non-zero remainder is 4. Therefore, GCF(12, 32) = 4.
The Euclidean algorithm is remarkably efficient and avoids the need for prime factorization, making it a powerful tool for finding the GCF of even very large numbers.
Illustrative Examples: Expanding the Concept
Let's expand our understanding by applying these methods to different pairs of numbers.
Example 1: Finding the GCF of 18 and 27
- Listing Factors: Factors of 18: 1, 2, 3, 6, 9, 18; Factors of 27: 1, 3, 9, 27; Common factors: 1, 3, 9; GCF: 9
- Prime Factorization: 18 = 2 x 3²; 27 = 3³; Common prime factor: 3; Lowest power: 3²; GCF: 9
- Euclidean Algorithm: 27 ÷ 18 = 1 remainder 9; 18 ÷ 9 = 2 remainder 0; GCF: 9
Example 2: Finding the GCF of 48 and 72
- Listing Factors: This becomes cumbersome for larger numbers.
- Prime Factorization: 48 = 2⁴ x 3; 72 = 2³ x 3²; Common prime factors: 2 and 3; Lowest powers: 2³ and 3; GCF: 2³ x 3 = 24
- Euclidean Algorithm: 72 ÷ 48 = 1 remainder 24; 48 ÷ 24 = 2 remainder 0; GCF: 24
The Significance of GCF in Real-World Applications
Beyond the realm of theoretical mathematics, the GCF finds practical applications in various fields:
- Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 12/32 can be simplified to 3/8 by dividing both the numerator and denominator by their GCF (4).
- Dividing Objects Equally: When dividing a collection of objects into smaller groups of equal size, the GCF determines the largest possible group size.
- Geometry and Measurement: The GCF plays a role in solving problems related to area, perimeter, and volume, allowing for the efficient division of shapes into smaller, congruent parts.
- Music Theory: The GCF is used in music theory to determine the greatest common divisor of two musical intervals, facilitating the understanding of harmonic relationships.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means that the numbers are relatively prime or coprime. They share no common factors other than 1.
Q2: Can the GCF of two numbers be larger than either number?
A2: No, the GCF of two numbers can never be larger than either of the numbers. It is always less than or equal to the smaller of the two numbers.
Q3: Is there a limit to the size of numbers for which the Euclidean Algorithm works?
A3: The Euclidean Algorithm works for any two integers, regardless of their size. It's a remarkably efficient algorithm that scales well to very large numbers.
Q4: Which method is best for finding the GCF?
A4: For smaller numbers, listing factors is a simple and intuitive method. For larger numbers, the Euclidean Algorithm is the most efficient method, while prime factorization provides a strong theoretical understanding.
Conclusion
Finding the greatest common factor of two numbers is a fundamental concept in mathematics with far-reaching applications. This guide explored three different methods for calculating the GCF, highlighting their strengths and weaknesses. Understanding these methods and their underlying principles empowers us to tackle more complex mathematical problems and appreciate the elegance and utility of number theory. Remember that choosing the right method depends on the numbers involved and your comfort level with different mathematical techniques. The goal is not only to find the answer but also to grasp the underlying concepts, which will serve as a solid foundation for future mathematical exploration. Through consistent practice and exploration, you can master the art of finding the GCF and unlock a deeper appreciation for the beauty and practicality of mathematics.
Latest Posts
Latest Posts
-
Centimeter To Square Feet Converter
Sep 15, 2025
-
1 14 As A Percent
Sep 15, 2025
-
18 Cm To Inches Conversion
Sep 15, 2025
-
43560 Square Feet To Miles
Sep 15, 2025
-
Converting Decimals Into Mixed Numbers
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.