Gcf Of 20 And 12
saludintensiva
Sep 13, 2025 · 6 min read
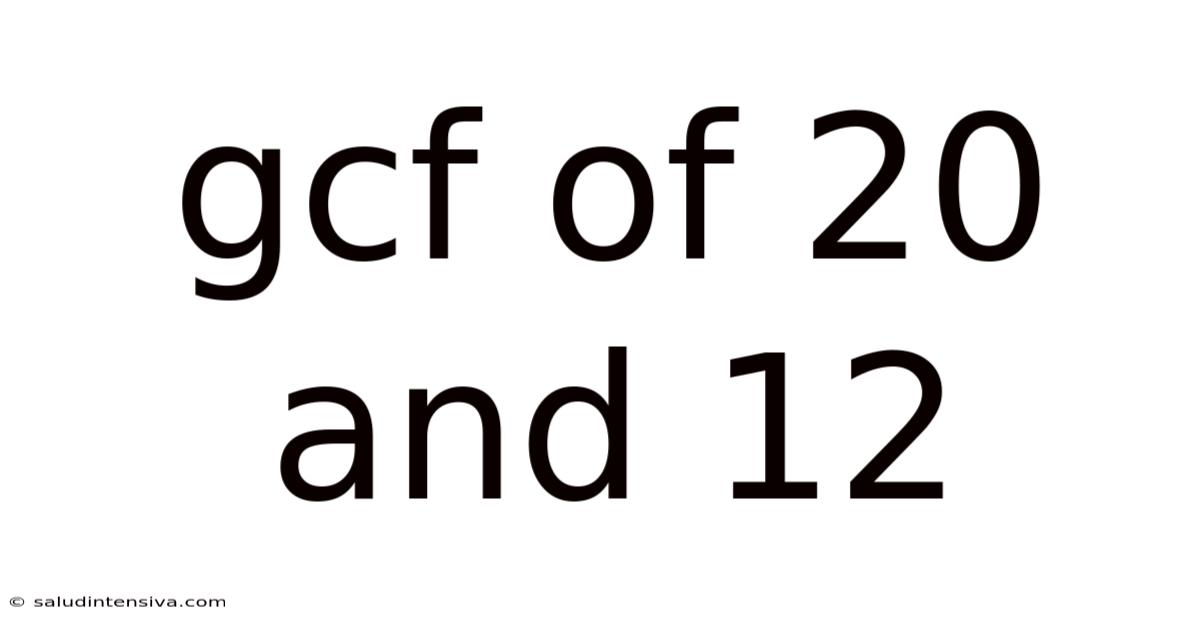
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 20 and 12: A Deep Dive
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the GCF reveals a deeper appreciation for number theory and its practical applications. This article will explore the GCF of 20 and 12, explaining multiple approaches, delving into the mathematical concepts involved, and addressing frequently asked questions. We'll move beyond simply stating the answer to provide a robust understanding of the GCF and its significance.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 20 are 1, 2, 4, 5, 10, and 20. The common factors of 12 and 20 are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 12 and 20 is 4.
Method 1: Listing Factors
This method, while straightforward, can become cumbersome for larger numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Steps:
- List the factors of 20: 1, 2, 4, 5, 10, 20
- List the factors of 12: 1, 2, 3, 4, 6, 12
- Identify the common factors: 1, 2, 4
- Determine the greatest common factor: 4
Therefore, the GCF of 20 and 12 is 4.
Method 2: Prime Factorization
This method is more efficient, particularly for larger numbers. It involves expressing each number as a product of its prime factors. The prime factorization of a number is its representation as a product of prime numbers.
Steps:
- Find the prime factorization of 20: 20 = 2 x 2 x 5 = 2² x 5
- Find the prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Identify common prime factors: Both 20 and 12 share two factors of 2 (2²).
- Multiply the common prime factors: 2 x 2 = 4
Therefore, the GCF of 20 and 12 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Steps:
- Start with the larger number (20) and the smaller number (12).
- Divide the larger number by the smaller number and find the remainder: 20 ÷ 12 = 1 with a remainder of 8.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (8).
- Repeat the division: 12 ÷ 8 = 1 with a remainder of 4.
- Repeat the process: 8 ÷ 4 = 2 with a remainder of 0.
- The last non-zero remainder is the GCF: 4
Therefore, the GCF of 20 and 12 is 4.
The Mathematical Significance of the GCF
The GCF is a fundamental concept in number theory with applications in various areas of mathematics and beyond:
- Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 20/12 can be simplified by dividing both the numerator and the denominator by their GCF (4), resulting in the equivalent fraction 5/3.
- Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a vital role in determining the solvability and finding solutions to these equations.
- Modular Arithmetic: The GCF is essential in modular arithmetic, which deals with remainders after division. It's used to determine the existence and uniqueness of solutions in modular congruences.
- Cryptography: The concept of GCF and its related concepts like least common multiple (LCM) are fundamental to modern cryptography. Algorithms like RSA rely on the difficulty of finding the GCF of very large numbers.
Applications of GCF in Real-World Scenarios
While the mathematical applications of GCF might seem abstract, it has practical applications in everyday life:
- Dividing Objects: If you have 20 apples and 12 oranges and want to divide them into equal groups, you can find the largest number of groups you can make (4 groups) with equal numbers of both fruits in each group.
- Measurement and Construction: In construction or carpentry, the GCF is useful for determining the largest common unit for cutting materials to avoid wastage.
- Scheduling: When scheduling events or tasks that occur at different intervals, the GCF can help determine the next time they coincide.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF be negative?
A: While technically, -4 also divides both 20 and 12, we typically only consider the positive greatest common factor. The GCF is always a positive integer.
Q: How do I find the GCF of more than two numbers?
A: You can extend any of the methods described above to find the GCF of more than two numbers. For instance, using prime factorization, find the prime factorization of each number and then multiply the common prime factors raised to the lowest power. The Euclidean algorithm can also be extended to handle more than two numbers.
Q: Is there a formula for calculating the GCF?
A: There isn't a single, universally applicable formula for calculating the GCF directly. However, the methods described above (listing factors, prime factorization, and the Euclidean algorithm) provide systematic ways to compute it.
Conclusion: More Than Just a Simple Calculation
Finding the greatest common factor of 20 and 12, while seemingly straightforward, opens a door to a deeper understanding of fundamental mathematical concepts. The various methods presented, from the simple listing of factors to the more sophisticated Euclidean algorithm, offer different approaches based on the numbers involved and the desired level of efficiency. The GCF's significance extends far beyond simple arithmetic, playing a vital role in various areas of mathematics and having practical applications in diverse real-world situations. This comprehensive exploration highlights its importance and its enduring relevance in the world of numbers. Understanding the GCF is not merely about finding an answer; it's about grasping the fundamental principles that underpin much of mathematics and its applications.
Latest Posts
Latest Posts
-
Boat Fuel Tank Size Calculator
Sep 13, 2025
-
70 Degrees Farenheit To Celcius
Sep 13, 2025
-
How Many Pounds 15 Kg
Sep 13, 2025
-
How Much Is Mcdonalds Tax
Sep 13, 2025
-
1 Divided By 1 2
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 20 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.