Gcf Of 32 And 20
saludintensiva
Sep 14, 2025 · 6 min read
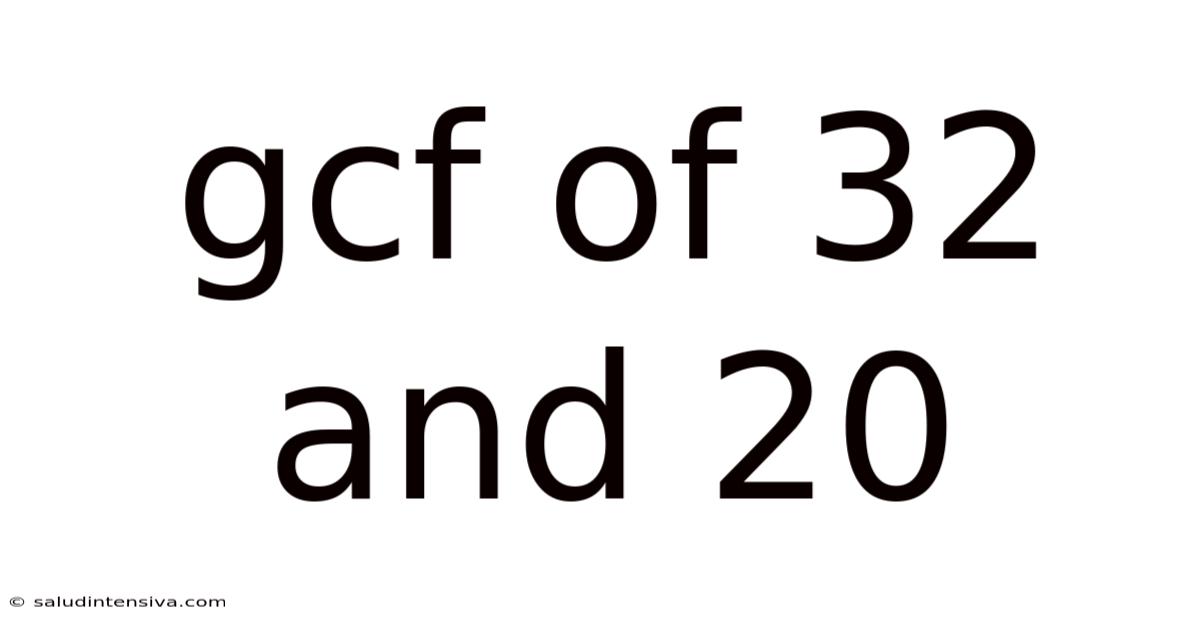
Table of Contents
Finding the Greatest Common Factor (GCF) of 32 and 20: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical problems. This comprehensive guide will explore various methods to determine the GCF of 32 and 20, explaining the underlying principles and providing practical examples to solidify your understanding. We'll delve into prime factorization, the Euclidean algorithm, and even explore the visual representation of GCF using Venn diagrams.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. This concept is important in various mathematical operations, especially when simplifying fractions or working with algebraic expressions.
Method 1: Prime Factorization
Prime factorization is a powerful method for finding the GCF of any two numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this method to find the GCF of 32 and 20:
1. Prime Factorization of 32:
32 can be broken down as follows:
- 32 = 2 x 16
- 16 = 2 x 8
- 8 = 2 x 4
- 4 = 2 x 2
Therefore, the prime factorization of 32 is 2 x 2 x 2 x 2 x 2 = 2⁵
2. Prime Factorization of 20:
20 can be broken down as follows:
- 20 = 2 x 10
- 10 = 2 x 5
Therefore, the prime factorization of 20 is 2 x 2 x 5 = 2² x 5
3. Identifying Common Factors:
Now, we compare the prime factorizations of 32 and 20:
32 = 2⁵ 20 = 2² x 5
The common factors are two 2's (2²).
4. Calculating the GCF:
The GCF is the product of the common prime factors raised to the lowest power. In this case, the common prime factor is 2, and the lowest power is 2².
Therefore, the GCF of 32 and 20 is 2² = 4.
Method 2: Listing Factors
This method is simpler for smaller numbers. We list all the factors of each number and then identify the largest common factor.
1. Factors of 32: 1, 2, 4, 8, 16, 32
2. Factors of 20: 1, 2, 4, 5, 10, 20
3. Common Factors: 1, 2, 4
4. Greatest Common Factor: The largest common factor is 4. Therefore, the GCF of 32 and 20 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
1. Start with the two numbers: 32 and 20
2. Divide the larger number (32) by the smaller number (20) and find the remainder:
32 ÷ 20 = 1 with a remainder of 12
3. Replace the larger number with the remainder: Now we work with 20 and 12.
4. Repeat the process:
20 ÷ 12 = 1 with a remainder of 8
5. Continue the process:
12 ÷ 8 = 1 with a remainder of 4
6. Final Step:
8 ÷ 4 = 2 with a remainder of 0
When the remainder is 0, the last non-zero remainder is the GCF. Therefore, the GCF of 32 and 20 is 4.
Visual Representation: Venn Diagram
A Venn diagram can visually represent the factors of two numbers and help identify the GCF. Let's create a Venn diagram for 32 and 20:
- Circle 1 (Factors of 32): 1, 2, 4, 8, 16, 32
- Circle 2 (Factors of 20): 1, 2, 4, 5, 10, 20
The overlapping section of the two circles represents the common factors: 1, 2, and 4. The largest number in the overlapping section is 4, which is the GCF.
Applications of GCF
The GCF has several practical applications in mathematics and beyond:
-
Simplifying Fractions: The GCF helps simplify fractions to their lowest terms. For example, the fraction 20/32 can be simplified by dividing both the numerator and the denominator by their GCF, which is 4: 20/32 = (20÷4) / (32÷4) = 5/8
-
Solving Algebraic Equations: GCF is used to factor algebraic expressions, making them easier to solve.
-
Measurement and Division Problems: Determining the largest possible equal sized pieces or groups. For example, if you have 32 red marbles and 20 blue marbles, and you want to divide them into equal groups of the same color, the largest number of groups you can make is 4 (the GCF of 32 and 20). Each group will contain 8 red marbles and 5 blue marbles.
-
Geometry and Area Calculations: Finding the largest square tile that can perfectly cover a rectangular area.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means they are relatively prime or coprime. This indicates that they don't share any common factors other than 1.
Q2: Can the GCF of two numbers be negative?
A2: No, the GCF is always a positive integer. We only consider the magnitude of the common factors.
Q3: Is there a difference between GCF and LCM?
A3: Yes, the least common multiple (LCM) is the smallest number that is a multiple of both numbers. The GCF and LCM are related by the formula: (GCF x LCM) = (Number 1 x Number 2). For 32 and 20, the LCM is 160. (4 x 160) = (32 x 20) = 640
Q4: Which method is best for finding the GCF?
A4: The best method depends on the numbers involved. For smaller numbers, listing factors is often easiest. For larger numbers, the Euclidean algorithm is more efficient. Prime factorization is a conceptually important method that provides insight into the structure of numbers.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with diverse applications. This guide has explored three primary methods – prime factorization, listing factors, and the Euclidean algorithm – providing a comprehensive understanding of how to determine the GCF of any two numbers, specifically highlighting the GCF of 32 and 20 which is 4. Understanding these methods empowers you to tackle more complex mathematical problems and strengthens your foundational knowledge in number theory. Remember to choose the method best suited to the numbers at hand, and don't hesitate to visualize the process using Venn diagrams for a clearer understanding. The ability to efficiently calculate the GCF is a valuable tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
60 Minutes In 1 Hour
Sep 14, 2025
-
1 2 3 Or 4
Sep 14, 2025
-
How Many Inches Is 18cm
Sep 14, 2025
-
Is 2 3 Larger Than 3 4
Sep 14, 2025
-
4 Out Of 5 Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 32 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.