Gcf Of 32 And 28
saludintensiva
Sep 14, 2025 · 6 min read
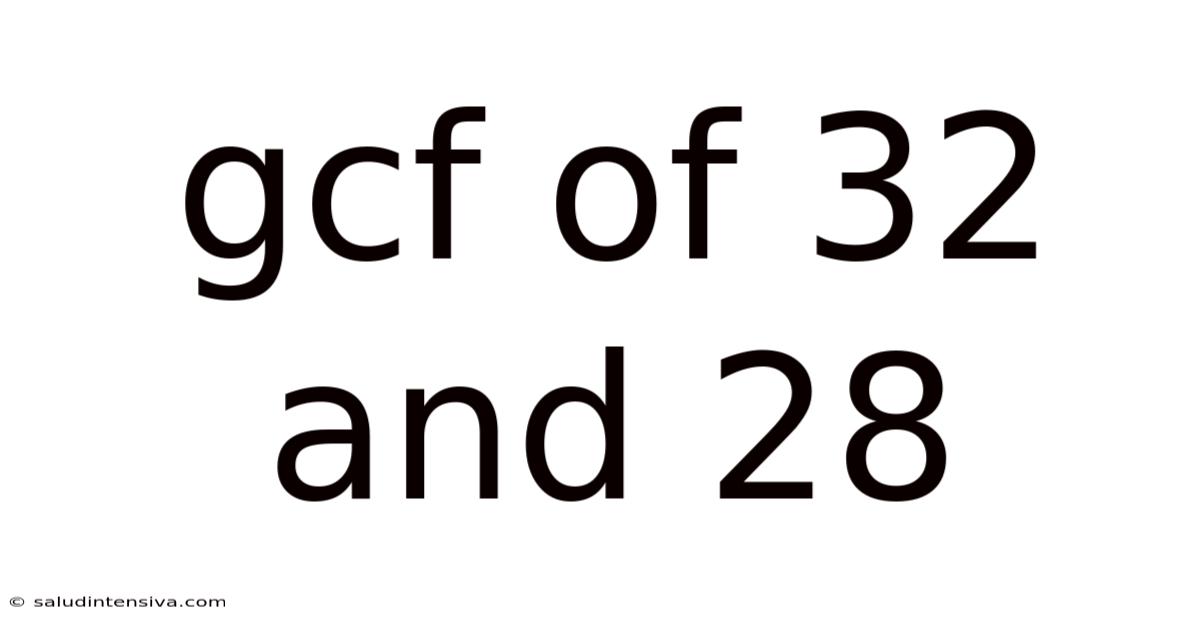
Table of Contents
Finding the Greatest Common Factor (GCF) of 32 and 28: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will explore various methods to determine the GCF of 32 and 28, delving into the underlying mathematical principles and providing a step-by-step guide suitable for learners of all levels. We'll go beyond a simple answer, exploring the broader implications and applications of finding the GCF, making this a valuable resource for anyone seeking a deeper understanding of this crucial mathematical concept.
Understanding the Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 32 and 28, let's establish a clear understanding of what the GCF represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. Understanding this definition is crucial to grasping the various methods used to find the GCF.
Method 1: Listing Factors
The most straightforward method for finding the GCF, especially for smaller numbers like 32 and 28, involves listing all the factors of each number and identifying the largest common factor.
Factors of 32: 1, 2, 4, 8, 16, 32 Factors of 28: 1, 2, 4, 7, 14, 28
By comparing the two lists, we can see that the common factors are 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 32 and 28 is 4.
This method is simple and intuitive, making it ideal for introductory learning. However, it becomes less efficient when dealing with larger numbers, as listing all factors can be time-consuming and prone to error.
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method for finding the GCF, particularly when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 32:
32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
Prime Factorization of 28:
28 = 2 x 14 = 2 x 2 x 7 = 2<sup>2</sup> x 7
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. In this case, the only common prime factor is 2, and its lowest power is 2<sup>2</sup> (or 4). Therefore, the GCF of 32 and 28 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 32 and 28:
- Step 1: Subtract the smaller number (28) from the larger number (32): 32 - 28 = 4
- Step 2: Now we find the GCF of 28 and 4. Subtract 4 repeatedly from 28 until we reach a number less than 4: 28 - 4 - 4 - 4 - 4 - 4 - 4 = 0. We subtracted 4 seven times.
- Since we reached 0 after subtracting 4 seven times from 28, the GCF is 4.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers. Its efficiency makes it a preferred method in computer programming for GCF calculations.
Applications of Finding the Greatest Common Factor
The concept of the GCF has far-reaching applications in various areas of mathematics and beyond. Here are a few examples:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For instance, the fraction 32/28 can be simplified by dividing both the numerator and denominator by their GCF (4), resulting in the simplified fraction 8/7.
-
Solving Word Problems: Many word problems involving quantities that need to be divided into equal groups rely on the GCF to find the largest possible size of the groups.
-
Algebra and Number Theory: GCF plays a vital role in more advanced mathematical concepts such as modular arithmetic, Diophantine equations, and abstract algebra.
-
Computer Science: The Euclidean algorithm, used for finding the GCF, is frequently used in computer science algorithms for tasks such as cryptography and data compression.
Further Exploration: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. There's a simple relationship between the GCF and LCM of two numbers (a and b):
LCM(a, b) * GCF(a, b) = a * b
Using this relationship, we can easily calculate the LCM of 32 and 28 once we know their GCF (which is 4):
LCM(32, 28) = (32 * 28) / 4 = 896 / 4 = 224
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be larger than either number?
A: No, the GCF of two numbers can never be larger than either of the numbers.
Q: Are there other methods for finding the GCF besides the ones mentioned?
A: Yes, there are other less commonly used methods such as the ladder method or using Venn diagrams for prime factorization visualization. However, the methods discussed above (listing factors, prime factorization, and the Euclidean algorithm) are the most efficient and widely used.
Q: Why is the Euclidean algorithm considered efficient?
A: The Euclidean algorithm's efficiency stems from its iterative nature; it reduces the problem to smaller equivalent subproblems until a solution is readily apparent. This makes it significantly faster than other methods for large numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill with widespread applications in mathematics and beyond. Understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – allows you to choose the most appropriate approach based on the numbers involved and your familiarity with each method. This article has aimed to provide a comprehensive understanding not only of how to find the GCF of 32 and 28 but also the broader significance of this concept within the realm of mathematics. By mastering the GCF, you're building a strong foundation for more advanced mathematical concepts and problem-solving skills. Remember that practice is key; the more you work with these methods, the more confident and efficient you will become.
Latest Posts
Latest Posts
-
What Is 80 Of 5
Sep 14, 2025
-
What Percent Is 15 20
Sep 14, 2025
-
What Percentage Is 1 4
Sep 14, 2025
-
3 To The 6th Power
Sep 14, 2025
-
11 Out Of 15 Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 32 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.