Gcf Of 60 And 90
saludintensiva
Sep 16, 2025 · 6 min read
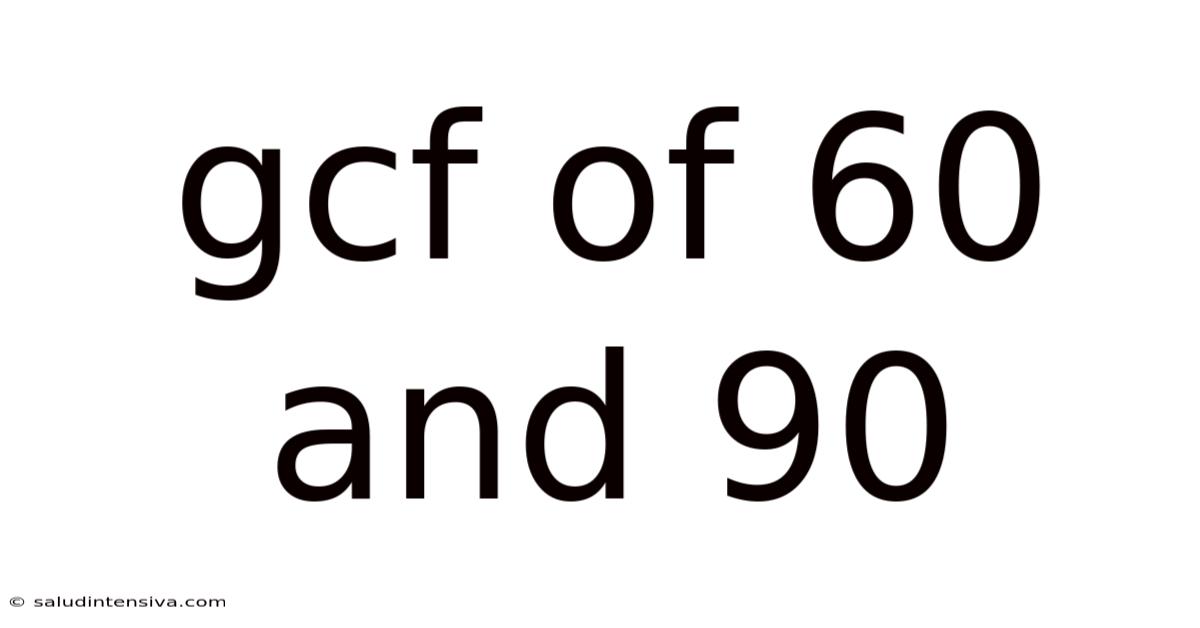
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 60 and 90: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring various methods for calculating the GCF opens a fascinating window into the world of number theory. This article delves into the process of finding the GCF of 60 and 90, exploring multiple approaches, their theoretical underpinnings, and practical applications. We will also address frequently asked questions and explore the broader significance of GCF in mathematics and beyond.
Introduction: Understanding the GCF
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial in various mathematical concepts, including simplification of fractions, solving equations, and understanding modular arithmetic. This article focuses on determining the GCF of 60 and 90 using several methods.
Method 1: Prime Factorization
This is arguably the most fundamental and conceptually clear method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 60
60 can be broken down as follows:
60 = 2 x 30 = 2 x 2 x 15 = 2 x 2 x 3 x 5 = 2² x 3 x 5
Step 2: Prime Factorization of 90
Similarly, let's find the prime factorization of 90:
90 = 2 x 45 = 2 x 3 x 15 = 2 x 3 x 3 x 5 = 2 x 3² x 5
Step 3: Identifying Common Factors
Now, compare the prime factorizations of 60 and 90:
60 = 2² x 3 x 5 90 = 2 x 3² x 5
The common prime factors are 2, 3, and 5.
Step 4: Calculating the GCF
To find the GCF, we take the lowest power of each common prime factor and multiply them together:
GCF(60, 90) = 2¹ x 3¹ x 5¹ = 30
Therefore, the greatest common factor of 60 and 90 is 30.
Method 2: Listing Factors
This method is straightforward but can be less efficient for larger numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Step 1: Factors of 60
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Step 2: Factors of 90
The factors of 90 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Step 3: Identifying Common Factors
Comparing the two lists, we find the common factors: 1, 2, 3, 5, 6, 10, 15, 30
Step 4: Determining the GCF
The largest common factor is 30. Therefore, the GCF(60, 90) = 30.
This method is simple to understand, but it becomes cumbersome when dealing with larger numbers with many factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Step 1: Initial Values
Let's start with a = 90 and b = 60.
Step 2: Repeated Subtraction (or Division with Remainder)
- Iteration 1: 90 = 1 * 60 + 30. The remainder is 30.
- Iteration 2: 60 = 2 * 30 + 0. The remainder is 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 30.
Therefore, GCF(60, 90) = 30.
The Euclidean algorithm is remarkably efficient, especially for larger numbers, because it significantly reduces the number of steps required compared to the listing factors method. The iterative nature of the algorithm makes it suitable for computer implementation.
Mathematical Explanation and Significance of the GCF
The GCF has profound implications in various areas of mathematics. Its calculation forms the basis for simplifying fractions. For example, the fraction 60/90 can be simplified to 2/3 by dividing both numerator and denominator by their GCF, which is 30. This simplification makes fractions easier to work with and understand.
The GCF also plays a significant role in modular arithmetic, which deals with remainders after division. Understanding the GCF helps in solving congruence equations and other problems related to modular arithmetic. Furthermore, the GCF is instrumental in determining the least common multiple (LCM) of two numbers. The LCM is the smallest positive integer that is a multiple of both numbers. The relationship between GCF and LCM is given by the formula:
GCF(a, b) * LCM(a, b) = a * b
In our case, GCF(60, 90) = 30. Therefore, LCM(60, 90) = (60 * 90) / 30 = 180.
Applications of the GCF Beyond the Classroom
The GCF is not merely a theoretical concept; it has practical applications in various fields:
- Geometry: The GCF is used to determine the dimensions of the largest possible square tiles that can be used to cover a rectangular area without any gaps or overlaps.
- Music: The GCF is used in music theory to find the greatest common divisor of note frequencies, aiding in the understanding of musical intervals and harmony.
- Computer Science: The GCF is applied in cryptography and computer algorithms for tasks like data compression and efficient computations.
- Engineering: In engineering design, the GCF can be used to find the optimal dimensions for components, ensuring efficient use of materials and minimizing waste.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they share no common factors other than 1.
Q2: Can the Euclidean Algorithm be used for more than two numbers?
A2: Yes, the Euclidean algorithm can be extended to find the GCF of more than two numbers. You would first find the GCF of two numbers, and then find the GCF of the result and the next number, and so on.
Q3: Is there a way to visually represent the GCF?
A3: Yes, Venn diagrams can effectively illustrate the concept of GCF. Each circle represents the prime factorization of a number, and the overlapping region represents the common factors.
Q4: How does the GCF relate to the Least Common Multiple (LCM)?
A4: The GCF and LCM are inversely related. A higher GCF implies a lower LCM, and vice versa. Their product always equals the product of the two original numbers.
Conclusion
Determining the GCF of 60 and 90, as explored through prime factorization, listing factors, and the Euclidean algorithm, is more than just a simple arithmetic exercise. It provides a gateway to understanding fundamental concepts in number theory, with applications extending far beyond the classroom. The methods described offer different approaches, each with its own strengths and weaknesses, making it crucial to understand the underlying principles to select the most efficient method based on the context. The GCF’s significance in various mathematical domains, and its surprising practical applications in diverse fields, underline its importance as a cornerstone of mathematical knowledge. By mastering the concept of the GCF, you not only enhance your mathematical skills but also gain a deeper appreciation for the interconnectedness of mathematical ideas and their relevance to the real world.
Latest Posts
Latest Posts
-
1 2 As A Mixed Number
Sep 16, 2025
-
Lcm Of 22 And 33
Sep 16, 2025
-
2 3 Acres To Square Feet
Sep 16, 2025
-
How Long Is 16 Hours
Sep 16, 2025
-
4 1 8 Improper Fraction
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 60 And 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.