Gcf Of 8 And 56
saludintensiva
Sep 13, 2025 · 6 min read
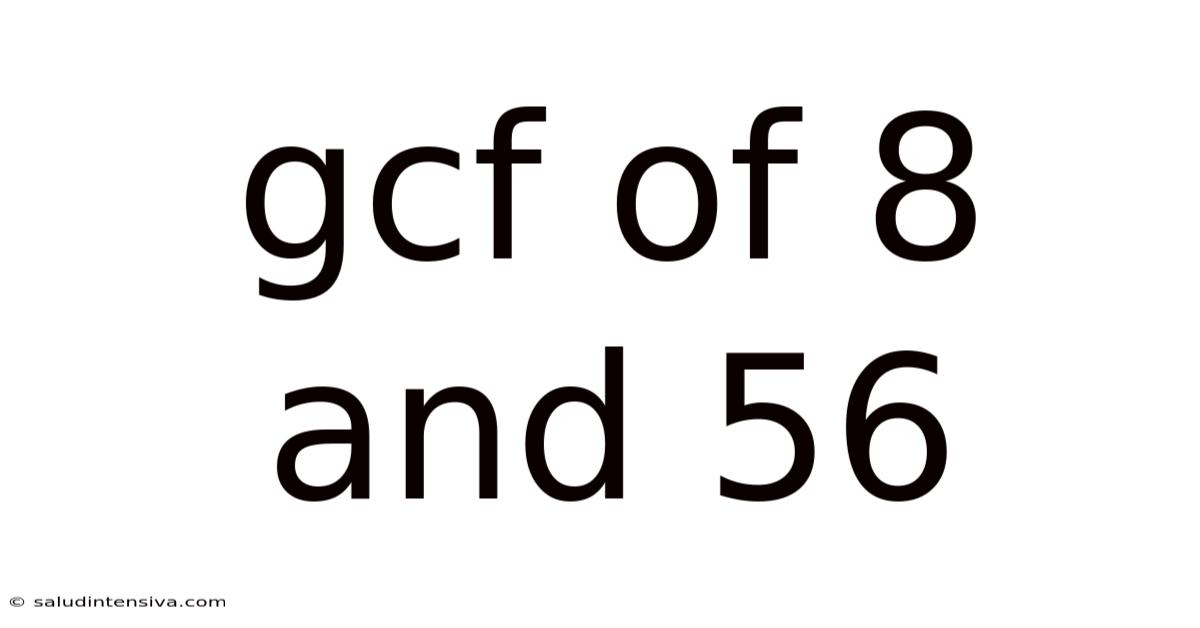
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 8 and 56: A Comprehensive Guide
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts provides a solid foundation for more advanced mathematical concepts. This comprehensive guide will delve into finding the GCF of 8 and 56, exploring various methods and explaining the underlying mathematical principles. We'll go beyond a simple answer and explore why this concept is crucial in mathematics and beyond. This will equip you with a thorough understanding, perfect for students, educators, and anyone curious about number theory.
Introduction: Understanding Greatest Common Factors
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The largest of these is 6, making 6 the GCF of 12 and 18. This seemingly simple concept forms the bedrock of many important mathematical operations.
This article focuses on finding the GCF of 8 and 56. While this may seem straightforward, understanding the different approaches will enhance your mathematical problem-solving skills. We'll explore several methods, from listing factors to using prime factorization and the Euclidean algorithm.
Method 1: Listing Factors
The most basic method for finding the GCF involves listing all the factors of each number and then identifying the largest common factor.
Factors of 8: 1, 2, 4, 8
Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
By comparing the two lists, we can see that the common factors of 8 and 56 are 1, 2, 4, and 8. The largest of these common factors is 8. Therefore, the GCF of 8 and 56 is 8.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger. Imagine trying to list all factors of 144 and 288 – it would be a time-consuming process! This highlights the need for more efficient methods for larger numbers.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). This method provides a more systematic approach, especially useful for larger numbers.
Let's find the prime factorization of 8 and 56:
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 56: 2 x 2 x 2 x 7 = 2³ x 7
Now, identify the common prime factors and their lowest powers. Both 8 and 56 share three factors of 2 (2³). Therefore, the GCF is 2³ = 8.
This method is significantly more efficient than listing factors, particularly when dealing with larger numbers. The prime factorization clearly shows the common building blocks of the numbers, making it easy to identify the GCF.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 8 and 56:
- Divide the larger number (56) by the smaller number (8): 56 ÷ 8 = 7 with a remainder of 0.
Since the remainder is 0, the smaller number (8) is the GCF. Therefore, the GCF of 8 and 56 is 8.
If the remainder wasn't 0, we would continue the process by replacing the larger number with the remainder and repeating the division until we reach a remainder of 0. This method is highly efficient and avoids the need for lengthy factorization or factor listing.
Mathematical Explanation and Significance of GCF
The concept of the GCF is deeply rooted in number theory and has numerous applications in various fields. Understanding the GCF helps us simplify fractions, solve problems involving divisibility, and work with modular arithmetic.
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, the fraction 56/8 can be simplified by dividing both the numerator and the denominator by their GCF, which is 8: 56/8 = (56÷8) / (8÷8) = 7/1 = 7.
-
Solving Divisibility Problems: The GCF helps determine if a number is divisible by another. If the GCF of two numbers is greater than 1, then they share a common divisor other than 1, meaning they are not relatively prime.
-
Modular Arithmetic: The GCF plays a crucial role in modular arithmetic, which deals with remainders after division. Understanding the GCF helps solve congruences and other problems in this area of mathematics.
-
Real-world Applications: While seemingly abstract, the concept of the GCF finds applications in various practical scenarios. For instance, in tiling a floor or arranging objects in rows and columns, understanding the GCF helps optimize the arrangement and minimize waste.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This signifies that they share no common factors other than 1.
Q2: Can the GCF of two numbers be larger than the smaller number?
A2: No, the GCF of two numbers can never be larger than the smaller of the two numbers. This is because the GCF must be a divisor of both numbers.
Q3: Which method is the most efficient for finding the GCF?
A3: For smaller numbers, listing factors can be efficient. However, for larger numbers, the Euclidean algorithm is generally the most efficient and reliable method. Prime factorization is a good compromise, offering a balance between efficiency and conceptual understanding.
Q4: Are there any online calculators or tools to find the GCF?
A4: While this article doesn't include links, many online calculators and tools are readily available to find the GCF of two or more numbers. These tools can be particularly helpful for larger numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill in mathematics, with applications extending far beyond simple arithmetic. Through understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – you gain a deeper appreciation for number theory and its practical implications. Remember to choose the method best suited to the numbers involved, prioritizing efficiency and understanding. Mastering the GCF opens doors to more advanced mathematical concepts and strengthens your problem-solving abilities across numerous disciplines. From simplifying fractions to understanding divisibility and modular arithmetic, the seemingly simple GCF holds a significant place in the broader mathematical landscape. So, next time you encounter a problem involving the GCF, you’ll be well-equipped to tackle it with confidence and understanding.
Latest Posts
Latest Posts
-
Lcm Of 24 And 21
Sep 13, 2025
-
2 To The 3 Power
Sep 13, 2025
-
What Time Is 21 40
Sep 13, 2025
-
27 Out Of 30 Percentage
Sep 13, 2025
-
1 3 Divided By 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 8 And 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.