Half Of 16 1 2
saludintensiva
Sep 18, 2025 · 6 min read
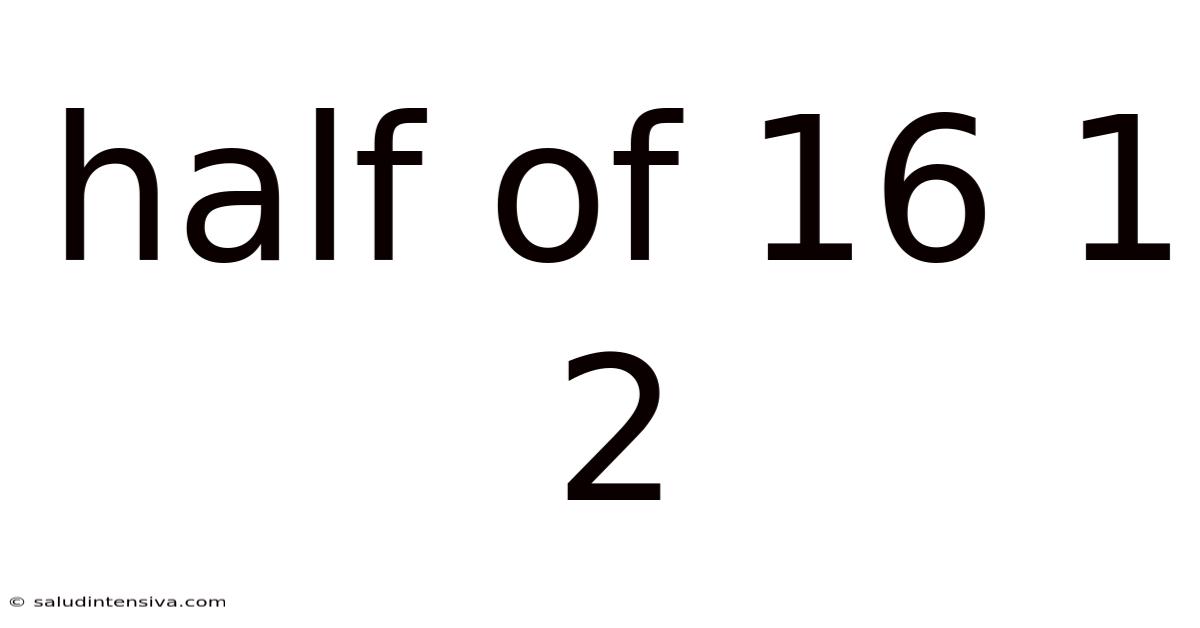
Table of Contents
Decoding "Half of 16 1/2": A Deep Dive into Fractions, Decimals, and Problem-Solving
This article explores the seemingly simple question, "What is half of 16 1/2?", but goes far beyond a simple answer. We'll delve into the fundamental mathematical concepts involved, providing a comprehensive understanding of fractions, decimals, and various problem-solving approaches. This exploration will equip you with skills applicable to more complex mathematical scenarios. Understanding this seemingly basic calculation opens doors to mastering more advanced concepts in arithmetic and beyond.
Introduction: Understanding the Problem
The question, "What is half of 16 1/2?" requires understanding fractions and how to perform operations involving them. At its core, it's a division problem: we need to divide 16 1/2 by 2. This seemingly straightforward problem offers a fantastic opportunity to explore several methods, highlighting different mathematical principles and solidifying your understanding of fractional arithmetic. We'll cover methods suitable for various levels of mathematical understanding, from elementary school to more advanced approaches.
Method 1: Converting to an Improper Fraction
This method is a cornerstone of fractional arithmetic. It involves converting the mixed number (16 1/2) into an improper fraction before performing the division.
-
Step 1: Convert the mixed number to an improper fraction. A mixed number consists of a whole number and a fraction (e.g., 16 1/2). To convert it to an improper fraction, we multiply the whole number by the denominator of the fraction and add the numerator. The result becomes the new numerator, while the denominator remains the same.
16 1/2 = (16 * 2 + 1) / 2 = 33/2
-
Step 2: Divide the improper fraction by 2. Dividing a fraction by a whole number is equivalent to multiplying the fraction by the reciprocal of the whole number. The reciprocal of 2 is 1/2.
(33/2) / 2 = (33/2) * (1/2) = 33/4
-
Step 3: Simplify the resulting fraction (if necessary). In this case, 33/4 is already in its simplest form.
-
Step 4: Convert back to a mixed number (optional). While 33/4 is a perfectly acceptable answer, we can convert it back to a mixed number for easier interpretation. To do this, divide the numerator (33) by the denominator (4):
33 ÷ 4 = 8 with a remainder of 1.
Therefore, 33/4 = 8 1/4
Therefore, half of 16 1/2 is 8 1/4.
Method 2: Working with the Whole Number and Fraction Separately
This method involves splitting the problem into two simpler calculations. We find half of the whole number and half of the fraction separately, then add the results.
-
Step 1: Find half of the whole number. Half of 16 is simply 16 / 2 = 8.
-
Step 2: Find half of the fraction. Half of 1/2 is (1/2) / 2 = 1/4. Alternatively, think of it as multiplying 1/2 by 1/2: (1/2) * (1/2) = 1/4.
-
Step 3: Add the results. Combine the results from steps 1 and 2: 8 + 1/4 = 8 1/4.
This method yields the same result: half of 16 1/2 is 8 1/4.
Method 3: Converting to Decimals
This approach utilizes decimal representation for easier calculation, especially for those more comfortable working with decimals.
-
Step 1: Convert the mixed number to a decimal. 16 1/2 is equivalent to 16.5 (since 1/2 = 0.5).
-
Step 2: Divide the decimal by 2. 16.5 / 2 = 8.25
-
Step 3: Convert the decimal back to a fraction (optional). 8.25 can be converted back to a fraction: 8.25 = 8 and 25/100 = 8 and 1/4 = 8 1/4.
Again, the answer remains 8 1/4.
The Importance of Understanding Different Methods
While all three methods produce the same correct answer, understanding each approach is crucial for developing strong mathematical skills. Method 1, using improper fractions, reinforces the fundamentals of fraction manipulation. Method 2 highlights the ability to break down complex problems into smaller, manageable parts. Method 3 showcases the flexibility of using decimals, which is essential in many real-world applications.
Expanding on the Concepts: Fractions and Decimals
This problem serves as an excellent foundation for understanding more complex fractional and decimal manipulations. Let's briefly review these concepts:
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Decimals: Decimals are another way to represent fractions, where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part.
Converting between Fractions and Decimals: Converting between fractions and decimals is a crucial skill. To convert a fraction to a decimal, simply divide the numerator by the denominator. To convert a decimal to a fraction, express the decimal as a fraction with a power of 10 as the denominator, and then simplify the fraction.
Practical Applications and Real-World Examples
The ability to calculate half of a mixed number, as demonstrated here, has countless practical applications. Consider these examples:
-
Cooking and Baking: Recipes often require halving or doubling ingredients. Understanding fraction manipulation is vital for accurate measurements.
-
Construction and Engineering: Precise measurements and calculations are critical in these fields. Working with fractions and decimals is essential for accuracy.
-
Finance and Budgeting: Understanding percentages and fractions is fundamental to managing personal finances, calculating interest, and understanding financial reports.
-
Data Analysis: Many data sets involve fractions and percentages. Being able to manipulate these effectively is crucial for interpreting data correctly.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this problem? A: Yes, a calculator can be used, but understanding the underlying mathematical principles is more important than simply getting the right answer. Using a calculator without comprehending the process limits your mathematical growth.
-
Q: What if the fraction wasn't 1/2? How would the process change? A: The process remains the same. You would simply use the appropriate fraction in your calculations, converting to an improper fraction or working with the whole number and fraction separately as needed.
-
Q: Are there other ways to solve this problem? A: While the methods outlined are the most common and efficient, other approaches exist depending on your mathematical background and preferred style. The key is to choose a method you understand and can apply consistently.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand and work with. It also ensures that your answer is in its most concise and accurate form.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is half of 16 1/2?", has opened a window into the world of fractions, decimals, and problem-solving strategies. By understanding different methods and their underlying principles, you've not just solved a single problem but have equipped yourself with valuable skills applicable to a wide range of mathematical challenges. Remember that mastering the fundamentals is key to tackling more complex problems with confidence and accuracy. The ability to confidently manipulate fractions and decimals is an invaluable asset in various aspects of life, extending far beyond the classroom. Continue practicing these skills, and you'll find your mathematical abilities growing exponentially.
Latest Posts
Latest Posts
-
Cubic Yard To Cubic Meter
Sep 18, 2025
-
2 5 8 In Decimal
Sep 18, 2025
-
How To Multiply Significant Figures
Sep 18, 2025
-
Hcf Of 9 And 12
Sep 18, 2025
-
23 4 As A Mixed Number
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Half Of 16 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.