How Many 1/4 Makes 1/3
saludintensiva
Sep 21, 2025 · 6 min read
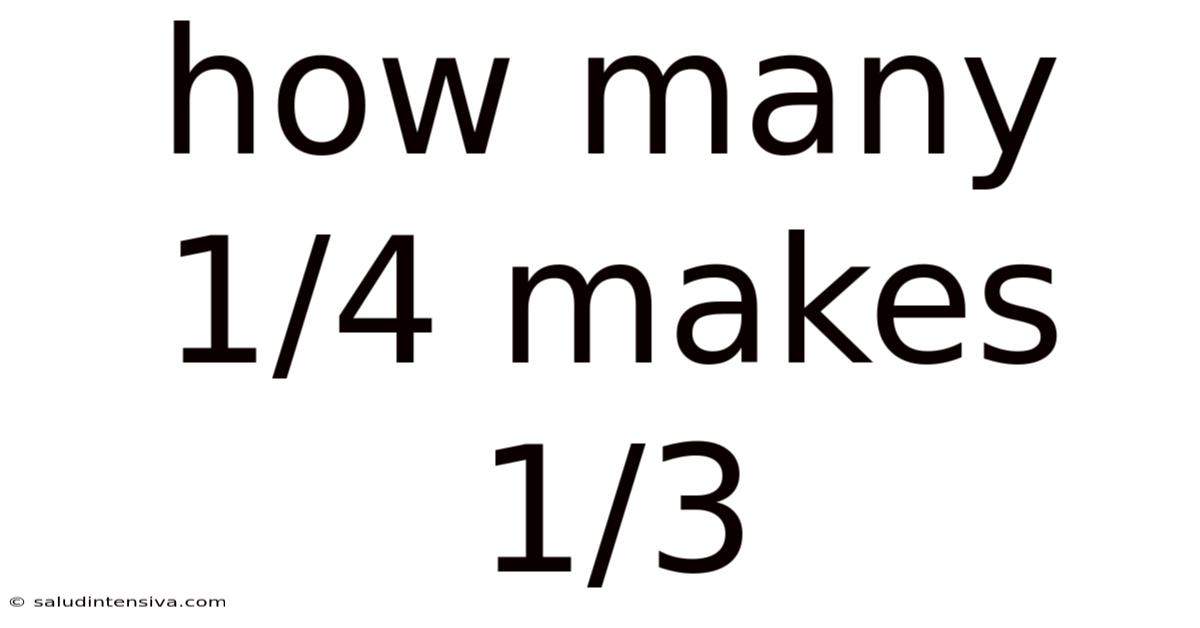
Table of Contents
How Many 1/4s Make 1/3? Unraveling Fractions and Their Relationships
Understanding fractions is a fundamental aspect of mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article delves into the seemingly simple question: "How many 1/4s make 1/3?" We'll not only solve this problem but also explore the underlying concepts of fractions, providing you with a deeper understanding of how they work and interact. This will equip you with the skills to tackle similar fraction problems with confidence.
Introduction: Understanding Fractions
Before diving into the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, 1/4 represents one part out of four equal parts.
This seemingly simple concept forms the basis for many mathematical operations. Adding, subtracting, multiplying, and dividing fractions all require a solid grasp of their fundamental nature. Our problem involves determining how many 1/4s are needed to equal 1/3. This requires understanding the relationship between these two fractions, which are expressed using different denominators.
Method 1: Using Division
The most straightforward approach to solving "how many 1/4s make 1/3?" is through division. We want to find out how many times 1/4 goes into 1/3. In mathematical terms, this translates to dividing 1/3 by 1/4:
(1/3) ÷ (1/4)
Dividing by a fraction is the same as multiplying by its reciprocal (flipping the fraction). The reciprocal of 1/4 is 4/1 or simply 4. Therefore, our calculation becomes:
(1/3) x (4/1) = 4/3
The result, 4/3, means that there are four-thirds of 1/4 in 1/3. This is an improper fraction, where the numerator is larger than the denominator. To make it easier to understand, we can convert it into a mixed number.
4/3 is equal to 1 and 1/3.
Therefore, one and one-third 1/4s make 1/3.
Method 2: Finding a Common Denominator
Another way to solve this problem is by finding a common denominator for both fractions. This involves converting both 1/3 and 1/4 into fractions with the same denominator. The least common multiple (LCM) of 3 and 4 is 12. Let's convert both fractions:
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 1/4 = (1 x 3) / (4 x 3) = 3/12
Now we can compare the two fractions. We can see that 4/12 is larger than 3/12. To find out how many 3/12s (1/4s) are in 4/12 (1/3), we divide 4/12 by 3/12:
(4/12) ÷ (3/12) = 4/3
This again gives us 4/3, confirming the result from Method 1. This method highlights the importance of equivalent fractions in solving problems involving different denominators.
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for those who find abstract mathematical concepts challenging. Imagine a pizza cut into 12 slices.
- 1/3 of the pizza represents 4 slices (12 slices / 3 = 4 slices).
- 1/4 of the pizza represents 3 slices (12 slices / 4 = 3 slices).
To figure out how many 1/4s (3 slices) are in 1/3 (4 slices), we can simply divide the number of slices representing 1/3 by the number of slices representing 1/4:
4 slices ÷ 3 slices = 4/3 slices
This visual method again confirms that 1/3 contains 4/3 or 1 and 1/3 of 1/4.
A Deeper Dive: Understanding Improper Fractions and Mixed Numbers
The solution to our problem, 4/3, is an improper fraction. An improper fraction is one where the numerator is greater than or equal to the denominator. These fractions represent values greater than or equal to 1. It's often more intuitive to express improper fractions as mixed numbers.
A mixed number consists of a whole number and a proper fraction (where the numerator is less than the denominator). Converting 4/3 to a mixed number involves dividing the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1.
This means 4/3 can be written as 1 and 1/3. This clearly shows that 1/3 contains one whole 1/4 and an additional 1/3 of a 1/4.
Practical Applications: Real-World Examples
Understanding fraction relationships has numerous practical applications. Here are a few examples:
- Cooking and Baking: Recipes often require precise measurements. If a recipe calls for 1/3 of a cup of flour, and you only have a 1/4 cup measuring cup, you'll need to use a little more than one 1/4 cup measurement.
- Construction and Engineering: Precision is paramount in construction and engineering. Calculations often involve fractions to ensure accurate measurements and building plans.
- Finance: Working with percentages and proportions in finance relies heavily on the understanding of fractions.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this using decimals? A: Yes, you can convert the fractions to decimals. 1/3 ≈ 0.333 and 1/4 = 0.25. Dividing 0.333 by 0.25 will give you approximately 1.333, which is close to 4/3 or 1 and 1/3. However, this method introduces rounding errors.
-
Q: What if the problem involved different fractions? A: The same principles apply. You can use division, find a common denominator, or use a visual method. The key is to understand the underlying concepts of fractions and their manipulation.
-
Q: Why is it important to understand this concept? A: Mastering fractions is essential for further mathematical studies, including algebra, geometry, and calculus. It also enhances problem-solving skills applicable in numerous real-world situations.
Conclusion: Mastering Fractions – A Building Block for Success
This article has explored the seemingly simple yet insightful question of how many 1/4s make 1/3. We’ve demonstrated three different methods to solve this problem, emphasizing the importance of understanding fundamental fraction concepts. Through division, finding a common denominator, and visual representation, we confirmed that 1/3 contains 1 and 1/3 of 1/4. This understanding extends beyond simple fraction problems, forming a solid foundation for more complex mathematical concepts and their practical applications in everyday life. Remember, consistent practice and a clear grasp of fundamental principles are key to mastering fractions and unlocking their potential in various fields.
Latest Posts
Latest Posts
-
One Thousand And Four Hundred
Sep 21, 2025
-
Expanded Form And Standard Form
Sep 21, 2025
-
Formula For Gravitational Kinetic Energy
Sep 21, 2025
-
Place Value Chart To Trillions
Sep 21, 2025
-
X 2 8x 12 Factor
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 Makes 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.