Is 1/2 Bigger Than 2/3
saludintensiva
Sep 14, 2025 · 5 min read
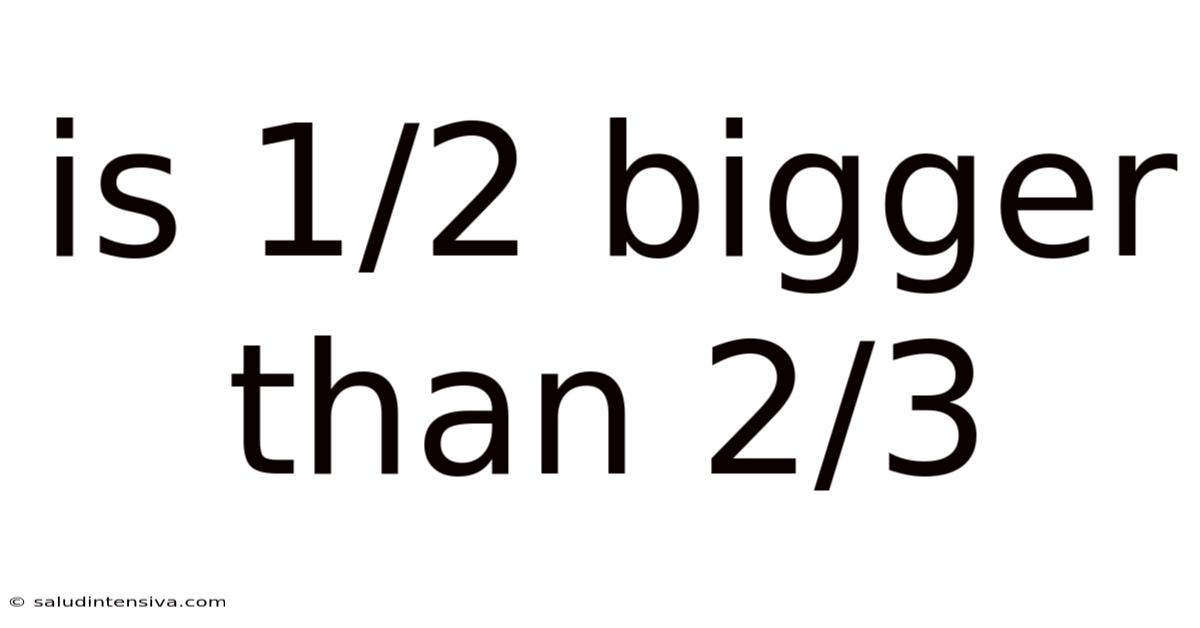
Table of Contents
Is 1/2 Bigger Than 2/3? Understanding Fractions and Comparisons
Understanding fractions is a fundamental skill in mathematics, crucial for navigating everyday tasks and more complex calculations. This article delves into the question, "Is 1/2 bigger than 2/3?", providing a comprehensive explanation that goes beyond a simple yes or no answer. We'll explore various methods for comparing fractions, solidify your understanding of fractional concepts, and even delve into the practical applications of these comparisons. This will equip you with the tools to confidently compare any two fractions.
Introduction: The Basics of Fractions
Before diving into the comparison of 1/2 and 2/3, let's refresh our understanding of what fractions represent. A fraction is a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we have.
For example, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts, and the numerator (1) indicates we have one of those parts. Similarly, in the fraction 2/3, the whole is divided into three equal parts, and we have two of them.
Method 1: Finding a Common Denominator
The most straightforward way to compare fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's compare 1/2 and 2/3:
-
Find the least common multiple (LCM) of the denominators 2 and 3. The LCM of 2 and 3 is 6.
-
Convert both fractions to have a denominator of 6:
-
To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
-
-
Compare the numerators: Now that both fractions have the same denominator, we can compare their numerators. We have 3/6 and 4/6. Since 3 < 4, we conclude that 3/6 < 4/6.
-
Therefore, 1/2 < 2/3. 1/2 is not bigger than 2/3.
Method 2: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. Imagine a circle or a rectangle representing the whole.
-
1/2: Divide the shape into two equal parts and shade one part.
-
2/3: Divide a separate, identical shape into three equal parts and shade two parts.
By visually comparing the shaded areas, it becomes apparent that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual confirmation reinforces the mathematical conclusion.
Method 3: Converting to Decimals
Another approach is to convert the fractions into decimals. This allows for a direct numerical comparison.
-
Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
-
Convert 2/3 to a decimal: 2 ÷ 3 = 0.666... (a repeating decimal)
Comparing 0.5 and 0.666..., it's clear that 0.666... is larger than 0.5. Therefore, 2/3 is greater than 1/2.
Method 4: Using Cross-Multiplication
Cross-multiplication is a quick method for comparing two fractions. This involves multiplying the numerator of one fraction by the denominator of the other, and vice versa.
-
Cross-multiply 1/2 and 2/3:
-
Multiply 1 (numerator of 1/2) by 3 (denominator of 2/3): 1 x 3 = 3
-
Multiply 2 (numerator of 2/3) by 2 (denominator of 1/2): 2 x 2 = 4
-
-
Compare the results: Since 3 < 4, the fraction with the smaller result (1/2) is the smaller fraction. Therefore, 1/2 < 2/3.
The Importance of Understanding Fraction Comparisons
The ability to compare fractions isn't just an academic exercise; it has practical applications in various aspects of life:
-
Cooking and Baking: Recipes often require precise measurements, and comparing fractions is essential for accurate ingredient proportions.
-
Construction and Engineering: In fields like construction and engineering, precise measurements and calculations are crucial for safety and functionality. Comparing fractions helps ensure accuracy in these areas.
-
Finance and Budgeting: Understanding fractions is vital for managing finances, calculating percentages, and understanding proportions in budgets and investments.
-
Data Analysis: In data analysis and statistics, fractions and their comparisons are fundamental for interpreting and presenting data effectively.
Frequently Asked Questions (FAQ)
Q: Why is finding a common denominator important?
A: Finding a common denominator allows us to directly compare the numerators of two fractions. This is because when fractions have the same denominator, they represent parts of the same sized whole. Comparing numerators then directly reflects the size of the fractional parts.
Q: Are there other ways to compare fractions besides the ones mentioned?
A: Yes, there are other methods, though less commonly used. These include using a number line or converting fractions to percentages.
Q: What if the fractions are mixed numbers (e.g., 1 1/2)?
A: To compare mixed numbers, you can either convert them to improper fractions (where the numerator is larger than the denominator) and then use any of the methods described above, or you can compare the whole number parts first and then compare the fractional parts if the whole numbers are equal.
Q: What if the fractions are negative?
A: When comparing negative fractions, remember that the further a number is from zero on the negative side, the smaller it is. For example, -1/2 is greater than -2/3 because -1/2 is closer to zero.
Q: Can I use a calculator to compare fractions?
A: Yes, many calculators can handle fraction calculations and comparisons. However, understanding the underlying principles is crucial for a deeper grasp of the concept.
Conclusion: Mastering Fraction Comparisons
Comparing fractions is a vital skill in mathematics with far-reaching practical applications. Whether you use the common denominator method, visual representation, decimal conversion, or cross-multiplication, understanding the underlying principles is key. This article has provided you with multiple methods to confidently compare fractions and a deeper understanding of what fractions represent. Practice these methods, and you'll soon be able to compare any two fractions with ease and accuracy. Remember that 1/2 is indeed smaller than 2/3 – a seemingly simple comparison that reveals fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Gcf Of 75 And 90
Sep 14, 2025
-
Hcf Of 15 And 18
Sep 14, 2025
-
Write 2 As A Decimal
Sep 14, 2025
-
Birth Calculator By Death Date
Sep 14, 2025
-
35 Degrees F To C
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Bigger Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.