Is 1/2 Equal To 2/3
saludintensiva
Sep 19, 2025 · 5 min read
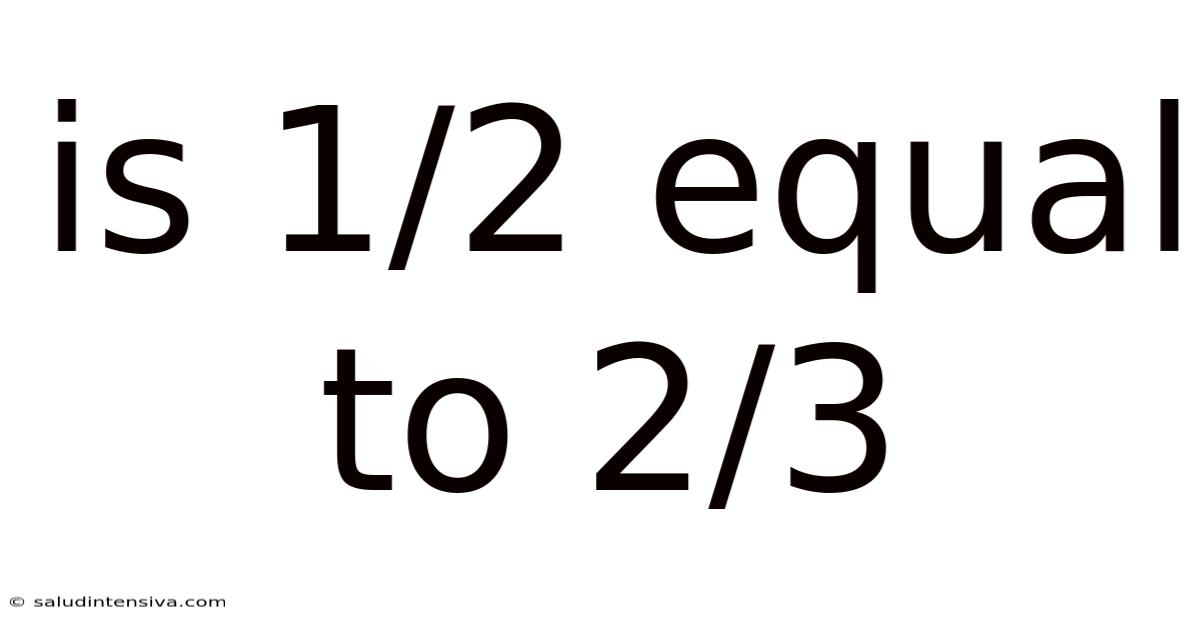
Table of Contents
Is 1/2 Equal to 2/3? Understanding Fractions and Equivalence
The question, "Is 1/2 equal to 2/3?" is a fundamental one in understanding fractions. At first glance, the answer might seem obvious: no. However, a deeper dive into the concept of fractions reveals a richer understanding of their representation and equivalence. This article will explore why 1/2 is not equal to 2/3, explain the concept of fraction equivalence, demonstrate methods for comparing fractions, and address common misconceptions.
Understanding Fractions: A Quick Refresher
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2, signifying one out of two equal parts.
Why 1/2 is Not Equal to 2/3
The simplest way to understand why 1/2 ≠ 2/3 is through visualization. Imagine a pizza cut into two equal slices. 1/2 represents one of those slices. Now, imagine a different pizza cut into three equal slices. 2/3 represents two of those three slices. Visually, it's clear that one slice of a two-slice pizza is not the same size as two slices of a three-slice pizza.
Numerically, we can compare fractions by finding a common denominator. This involves converting both fractions to equivalent fractions with the same denominator. The least common denominator (LCD) of 2 and 3 is 6. Therefore:
- 1/2 can be converted to 3/6 (multiply both numerator and denominator by 3).
- 2/3 can be converted to 4/6 (multiply both numerator and denominator by 2).
Since 3/6 is clearly less than 4/6, we can definitively say that 1/2 is not equal to 2/3.
The Concept of Fraction Equivalence
While 1/2 and 2/3 are not equal, the concept of equivalent fractions is crucial in understanding fractions. Equivalent fractions represent the same portion of a whole, even though they have different numerators and denominators. You can create equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example:
- 1/2 = 2/4 = 3/6 = 4/8 = 5/10 and so on. All these fractions represent half of a whole.
This principle is based on the property of ratios. Multiplying or dividing both parts of a ratio by the same number doesn't change the ratio's value.
Methods for Comparing Fractions
Several methods exist for comparing fractions to determine which is larger or smaller:
-
Finding a Common Denominator: As demonstrated earlier, this is a reliable method. Convert both fractions to equivalent fractions with the same denominator and then compare the numerators. The fraction with the larger numerator is the larger fraction.
-
Cross-Multiplication: This method is a shortcut for comparing two fractions. Cross-multiply the numerator of one fraction by the denominator of the other, and vice versa. The fraction whose cross-product is larger is the larger fraction. For example, comparing 1/2 and 2/3:
- 1 x 3 = 3
- 2 x 2 = 4
Since 4 > 3, 2/3 is larger than 1/2.
-
Converting to Decimals: Convert both fractions to decimals by dividing the numerator by the denominator. Then compare the decimal values. For example:
- 1/2 = 0.5
- 2/3 ≈ 0.667
Since 0.667 > 0.5, 2/3 is larger than 1/2.
Visual Representations: Helping to Understand Fractions
Visual aids are incredibly helpful, especially for beginners. Using diagrams like circles, rectangles, or number lines can make abstract concepts more concrete. Dividing a shape into equal parts and shading the appropriate number of parts helps visualize the fraction's value. This visual approach clarifies the difference between 1/2 and 2/3, demonstrating that they represent different portions of a whole.
Addressing Common Misconceptions
Several common misconceptions surround fractions:
-
Focusing solely on the numerator or denominator: Students might incorrectly assume that the larger numerator always indicates the larger fraction, ignoring the denominator.
-
Difficulty finding a common denominator: Finding the least common denominator can be challenging. Practicing finding the least common multiple (LCM) of numbers helps overcome this hurdle.
-
Misunderstanding equivalent fractions: Some students struggle to grasp the concept that equivalent fractions represent the same value. Repeated practice with creating equivalent fractions is essential.
Further Exploration: Beyond Basic Comparisons
The principles discussed here are foundational. Once you master comparing simple fractions, you can progress to more complex concepts:
-
Comparing mixed numbers: Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). Converting mixed numbers to improper fractions (where the numerator is larger than the denominator) simplifies comparison.
-
Comparing fractions with different denominators and numerators: Mastering the techniques mentioned above will help in tackling more challenging fraction comparisons.
-
Ordering fractions: Arrange a set of fractions in ascending or descending order using the comparison techniques discussed.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be compared using these methods? A: Yes, these methods are applicable to all fractions, including those with larger numerators and denominators.
-
Q: Is there a quickest method for comparing fractions? A: The "quickest" method depends on individual preference and the specific fractions involved. Cross-multiplication is often efficient for simple comparisons, while converting to decimals might be faster for complex fractions.
-
Q: Why is understanding fraction equivalence important? A: Understanding fraction equivalence is crucial for performing arithmetic operations (addition, subtraction, multiplication, and division) with fractions. It allows for simplification and finding common denominators.
-
Q: How can I improve my understanding of fractions? A: Consistent practice with various exercises, using visual aids, and seeking help when needed are key. Working through problems of increasing complexity builds a strong foundation.
Conclusion: Mastering the Fundamentals of Fractions
In conclusion, 1/2 is definitively not equal to 2/3. This article has explained the reasons behind this inequality and provided a thorough exploration of the fundamental concepts related to fractions. Understanding fractions, including equivalence and comparison methods, is crucial for mathematical proficiency. By mastering these concepts, students can build a solid foundation for more advanced mathematical topics. Remember that consistent practice and a clear understanding of the underlying principles are essential to developing fluency and confidence in working with fractions. Through visualization, numerical methods, and a persistent approach to learning, anyone can overcome the challenges posed by fractions and unlock their mathematical potential.
Latest Posts
Latest Posts
-
Amortization Calculator With Quarterly Payments
Sep 19, 2025
-
2 Out Of 3 Percentage
Sep 19, 2025
-
Square Root Of 1 9
Sep 19, 2025
-
Row 20 Of Pascals Triangle
Sep 19, 2025
-
Gcf Of 64 And 56
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Equal To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.