Square Root Of 1 9
saludintensiva
Sep 19, 2025 · 5 min read
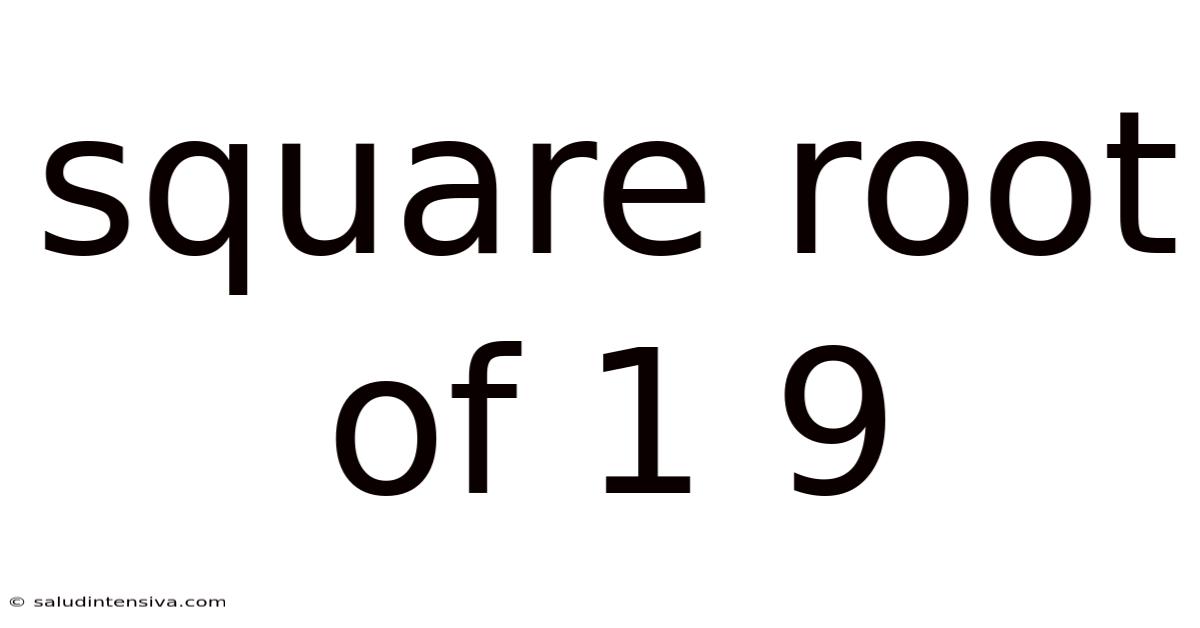
Table of Contents
Delving Deep into the Square Root of 19: A Comprehensive Exploration
The square root of 19, denoted as √19, is an irrational number, meaning it cannot be expressed as a simple fraction. This seemingly simple concept opens up a fascinating world of mathematical exploration, encompassing various methods of approximation, its practical applications, and its deeper theoretical significance within the broader field of number theory. This article aims to provide a comprehensive understanding of √19, suitable for readers with varying mathematical backgrounds, from beginners to those with a stronger grasp of numerical concepts. We will explore different approaches to calculating its value, examine its properties, and discuss its relevance in diverse areas.
Understanding Square Roots: A Foundational Overview
Before we delve into the specifics of √19, let's establish a firm understanding of what a square root represents. The square root of a number x is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. However, things become more complex when dealing with numbers that aren't perfect squares – numbers that cannot be obtained by squaring an integer. 19 falls into this category.
This is where the concept of irrational numbers comes into play. Irrational numbers are numbers that cannot be expressed as a fraction of two integers (a/b, where 'a' and 'b' are integers and b≠0). Their decimal representations are non-terminating and non-repeating. √19 is an irrational number, meaning its decimal expansion continues infinitely without any repeating pattern.
Methods for Approximating √19
Since √19 is irrational, we cannot obtain its exact value. Instead, we rely on approximation techniques. Several methods can be employed, each with its own level of accuracy and complexity:
1. The Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an iterative algorithm that refines an initial guess to progressively closer approximations of the square root. The formula is:
x<sub>n+1</sub> = ½ (x<sub>n</sub> + a/x<sub>n</sub>)
where:
- x<sub>n</sub> is the nth approximation
- a is the number whose square root we're seeking (in our case, 19)
- x<sub>n+1</sub> is the next, improved approximation
Let's illustrate this with an initial guess of 4 (since 4² = 16, it's close to 19):
- Iteration 1: x<sub>1</sub> = ½ (4 + 19/4) = 4.25
- Iteration 2: x<sub>2</sub> = ½ (4.25 + 19/4.25) ≈ 4.35889
- Iteration 3: x<sub>3</sub> = ½ (4.35889 + 19/4.35889) ≈ 4.3588989
As you can see, the approximation rapidly converges to a value close to the actual square root of 19. With each iteration, the precision increases significantly. This method is computationally efficient and converges quickly, making it suitable for computer algorithms.
2. Using a Calculator or Computer Software: The Easiest Approach
The simplest and most practical method for approximating √19 is to use a calculator or computer software. These tools employ sophisticated algorithms, often variations of the Babylonian method or other advanced techniques, to calculate square roots to a high degree of accuracy. Most calculators will provide an approximation of √19 to several decimal places (approximately 4.3589).
3. Linear Interpolation: A Simpler, Less Accurate Method
A simpler, albeit less accurate, method is linear interpolation. This involves finding the square root of the nearest perfect squares and using a proportion to estimate the value. Since 19 lies between 16 (4²) and 25 (5²), we can approximate as follows:
√19 is approximately 4 + (19-16)/(25-16) * (5-4) = 4 + 3/9 ≈ 4.33
While this method is less precise than the Babylonian method or calculator approximation, it provides a quick, rough estimate.
The Significance of √19 in Mathematics and Beyond
While √19 might seem like a relatively insignificant number, its presence within mathematical frameworks is far-reaching:
-
Irrational Numbers and Number Theory: √19 serves as a prime example of an irrational number, illustrating the vastness of the real number system and the complexities of number theory. Its irrationality underscores the inherent limits of representing all numbers as fractions.
-
Algebra and Quadratic Equations: √19 appears frequently in solutions to quadratic equations. For instance, the equation x² - 19 = 0 has solutions x = ±√19. These equations are fundamental tools in numerous fields, including physics and engineering.
-
Geometry and Trigonometry: Square roots, including √19, frequently show up in geometrical calculations, particularly when dealing with lengths, areas, and volumes involving non-right angled triangles. Trigonometric functions also incorporate square roots in their formulations.
-
Calculus and Analysis: The concept of limits and derivatives in calculus often involves working with irrational numbers like √19. These principles underpin the study of continuous change and are essential tools in various scientific disciplines.
Frequently Asked Questions (FAQs)
Q: Is √19 a rational or irrational number?
A: √19 is an irrational number. It cannot be expressed as a fraction of two integers and has a non-terminating, non-repeating decimal representation.
Q: How can I calculate √19 without a calculator?
A: You can use approximation methods like the Babylonian method (Heron's method) to estimate √19. However, these methods are iterative and require multiple calculations. Linear interpolation offers a simpler, but less accurate, alternative.
Q: What are the practical applications of √19?
A: √19, like other irrational numbers, finds applications in various fields, including physics (e.g., calculating distances or velocities), engineering (e.g., solving structural problems), and computer graphics (e.g., generating realistic curves). Its role is often indirect, embedded within broader mathematical models and equations.
Q: Can √19 be simplified further?
A: No, √19 cannot be simplified further because 19 is a prime number. It does not have any perfect square factors other than 1.
Conclusion: A Number Beyond Simple Representation
The square root of 19, while seemingly a simple mathematical concept, encapsulates a wealth of mathematical ideas and practical implications. Its irrationality underscores the complexities of the number system, highlighting the limitations of representing all numbers as simple fractions. While we cannot express its exact value, the various approximation methods available showcase the ingenuity of mathematical thought. From the iterative precision of the Babylonian method to the readily available accuracy of calculators, the quest for understanding √19 provides a fascinating glimpse into the world of numerical analysis and its widespread relevance across diverse fields. The exploration of √19 serves not only as a calculation exercise but also as a testament to the beauty and depth inherent within the seemingly simple world of numbers.
Latest Posts
Latest Posts
-
Gcf For 6 And 8
Sep 19, 2025
-
2 3 Divided By 15
Sep 19, 2025
-
1 Divided By 1 4
Sep 19, 2025
-
6 1 4 3 5 8
Sep 19, 2025
-
4 To The Power 5
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.