Is 1/2 Greater Than 2/3
saludintensiva
Sep 17, 2025 · 5 min read
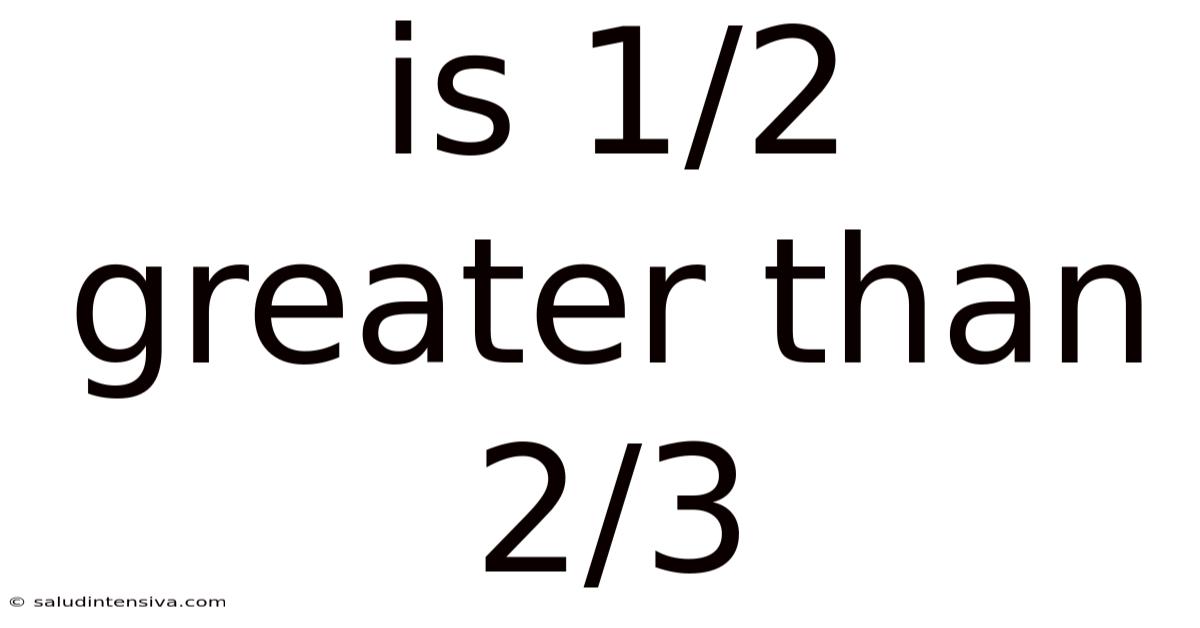
Table of Contents
Is 1/2 Greater Than 2/3? Understanding Fractions and Comparisons
This article delves into the seemingly simple question: Is 1/2 greater than 2/3? While the answer might seem obvious to some, understanding the underlying principles of fraction comparison is crucial for developing a strong foundation in mathematics. We will explore various methods for comparing fractions, providing a clear and comprehensive explanation suitable for learners of all levels. This includes visual representations, numerical comparisons, and a deeper look at the concepts of numerators and denominators. By the end, you'll not only know the answer but also possess the tools to confidently compare any two fractions.
Understanding Fractions: A Quick Recap
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2. This means we have 1 out of 2 equal parts.
Visualizing Fractions: The Power of Pictures
One of the most effective ways to compare fractions is to visualize them. Imagine a circle divided into equal parts. For 1/2, we divide the circle into two equal halves and shade one of them. For 2/3, we divide the circle into three equal parts and shade two of them. By visually comparing the shaded areas, it becomes immediately apparent that 2/3 represents a larger portion of the circle than 1/2.
[Here, ideally, we would insert two images. One showing a circle divided into two halves with one half shaded (representing 1/2) and another showing a circle divided into three parts with two parts shaded (representing 2/3). Since I cannot insert images directly, please imagine these visuals.]
Comparing Fractions: Three Key Methods
There are several ways to compare fractions numerically, even without resorting to visualizations:
1. Finding a Common Denominator: This is the most common and reliable method. To compare 1/2 and 2/3, we need to find a common denominator, which is a number that both 2 and 3 divide into evenly. The least common multiple of 2 and 3 is 6. We then rewrite each fraction with a denominator of 6:
- 1/2 = (1 x 3) / (2 x 3) = 3/6
- 2/3 = (2 x 2) / (3 x 2) = 4/6
Now, comparing 3/6 and 4/6 is straightforward. Since 4 > 3, we conclude that 2/3 > 1/2.
2. Converting to Decimals: Another approach is to convert each fraction into its decimal equivalent. This involves dividing the numerator by the denominator:
- 1/2 = 1 ÷ 2 = 0.5
- 2/3 = 2 ÷ 3 ≈ 0.667
Since 0.667 > 0.5, we again confirm that 2/3 > 1/2.
3. Cross-Multiplication: This method is particularly useful for quick comparisons. We cross-multiply the numerators and denominators of the two fractions:
- (1 x 3) = 3
- (2 x 2) = 4
Since 4 > 3, we conclude that 2/3 > 1/2. The larger product corresponds to the larger fraction.
A Deeper Dive into Numerators and Denominators
The relationship between the numerator and denominator is crucial in understanding the value of a fraction. A larger numerator with the same denominator means a larger fraction (e.g., 3/4 > 1/4). Conversely, a smaller denominator with the same numerator means a larger fraction (e.g., 1/2 > 1/4). When comparing fractions with different numerators and denominators, finding a common denominator or using cross-multiplication allows us to make a direct comparison.
Addressing Common Misconceptions
A common mistake is to assume that because the numerator of 2/3 is larger than the numerator of 1/2, 2/3 is automatically the larger fraction. This is incorrect without considering the denominators. The denominator plays a crucial role in determining the size of each fraction.
Real-World Applications of Fraction Comparison
Comparing fractions isn't just an abstract mathematical exercise; it has practical applications in many real-world situations. Imagine you're choosing between two cakes: one is 1/2 eaten, and the other is 2/3 eaten. Knowing how to compare fractions helps you quickly determine which cake has more left. This skill extends to various fields, including cooking, construction, and even financial calculations.
Extending the Concept: Comparing More Than Two Fractions
The methods discussed above can be extended to compare more than two fractions. For example, to compare 1/2, 2/3, and 3/5, we can find a common denominator (30 in this case) and rewrite each fraction with that denominator:
- 1/2 = 15/30
- 2/3 = 20/30
- 3/5 = 18/30
By comparing the numerators, we find that 2/3 > 3/5 > 1/2.
Frequently Asked Questions (FAQ)
Q: What if the fractions are already in their simplest form? Do I still need to find a common denominator?
A: While it’s not strictly necessary if one fraction is clearly larger or smaller, finding a common denominator remains the most reliable method for ensuring accuracy, especially when the difference between fractions is small.
Q: Is there a quick way to estimate which fraction is larger without performing calculations?
A: Sometimes, you can make a reasonable estimation by looking at the fractions. For example, 1/2 is easily recognized as 0.5. If the other fraction is clearly above or below 0.5, that can provide a quick estimate. However, this method is not always accurate.
Q: Are there any online tools or calculators that can help me compare fractions?
A: While I cannot provide links to external websites, many online resources and calculators are readily available to assist with fraction comparison and other mathematical calculations. A simple internet search should yield numerous options.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. By understanding the concepts of numerators and denominators and employing the methods described in this article – finding a common denominator, converting to decimals, or cross-multiplication – you can confidently compare any two fractions. This skill is not only essential for academic success but also has widespread practical applications in everyday life. Remember to visualize the fractions when possible; it can greatly aid your understanding and make the comparison process more intuitive. Practice regularly to build your confidence and proficiency in comparing fractions.
Latest Posts
Latest Posts
-
260 Billion In Scientific Notation
Sep 17, 2025
-
Answer To A Multiplication Problem
Sep 17, 2025
-
2 3 Plus 1 6
Sep 17, 2025
-
What Is 200db Depreciation Method
Sep 17, 2025
-
4 To Power Of 8
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.