Is 1/3 Greater Than 1/2
saludintensiva
Sep 14, 2025 · 5 min read
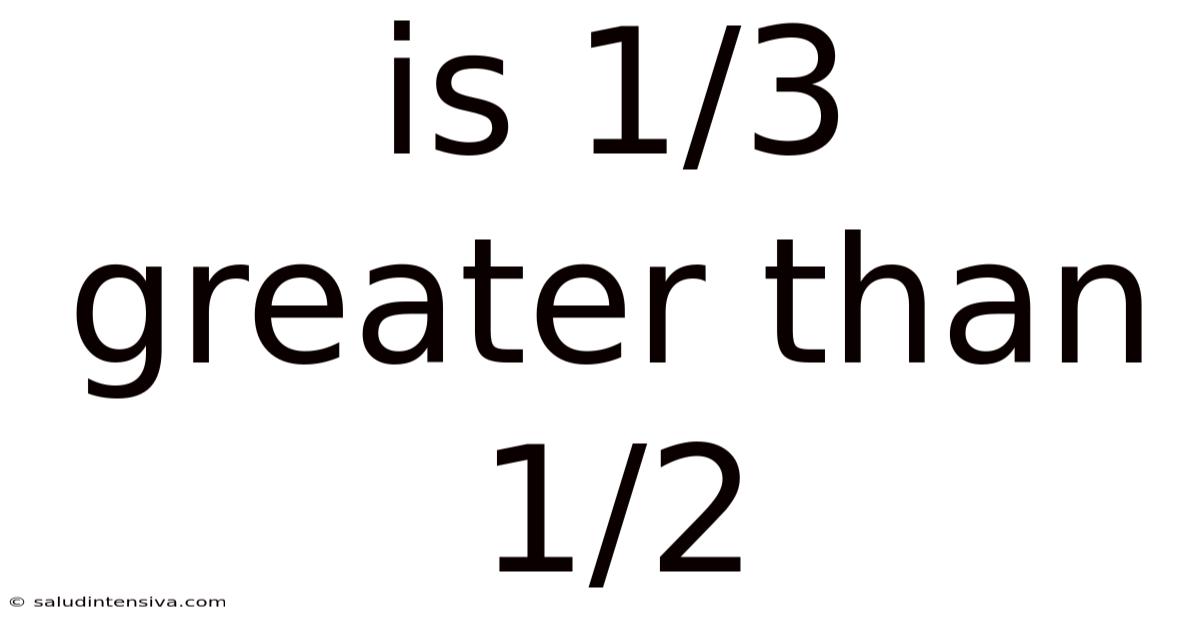
Table of Contents
Is 1/3 Greater Than 1/2? Understanding Fractions and Comparisons
Many people find fractions challenging, and comparing them can seem even more daunting. A common question that often arises is: is 1/3 greater than 1/2? This article will not only answer that question definitively but also provide a thorough understanding of fractions, offering various methods to compare them, and addressing common misconceptions. We'll delve into the underlying mathematical principles and provide practical examples to solidify your comprehension.
Understanding Fractions: A Quick Refresher
Before we dive into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where:
- 'a' is the numerator: This represents the number of parts we have.
- 'b' is the denominator: This represents the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) indicates we have one part, and the denominator (2) indicates the whole is divided into two equal parts. This means we have half of the whole.
Comparing 1/3 and 1/2: Visual Representation
One of the easiest ways to compare fractions is through visual representation. Imagine two identical circles.
- Circle 1: Divide this circle into two equal halves. Shade one half. This represents 1/2.
- Circle 2: Divide this circle into three equal thirds. Shade one third. This represents 1/3.
By visually comparing the shaded areas, it's immediately clear that the shaded area in Circle 1 (1/2) is larger than the shaded area in Circle 2 (1/3). Therefore, 1/3 is not greater than 1/2; 1/2 is greater than 1/3.
Comparing Fractions: Numerical Methods
While visual representation is helpful for understanding, numerical methods are crucial for more complex fraction comparisons. Here are three primary methods:
1. Finding a Common Denominator
This is a fundamental method for comparing fractions. To compare 1/3 and 1/2, we need to find a common denominator – a number that both 3 and 2 divide into evenly. The least common multiple (LCM) of 3 and 2 is 6.
- We convert 1/2 to an equivalent fraction with a denominator of 6: (1 x 3) / (2 x 3) = 3/6
- We convert 1/3 to an equivalent fraction with a denominator of 6: (1 x 2) / (3 x 2) = 2/6
Now we can easily compare: 3/6 > 2/6. Therefore, 1/2 > 1/3.
2. Converting to Decimals
Converting fractions to decimals allows for a direct numerical comparison.
- 1/2 = 0.5
- 1/3 = 0.333... (a repeating decimal)
Clearly, 0.5 > 0.333..., confirming that 1/2 > 1/3.
3. Using Cross-Multiplication
This method is particularly useful when comparing fractions with different numerators and denominators. We cross-multiply the numerators and denominators:
- 1/3 and 1/2
- (1 x 2) and (3 x 1) which gives us 2 and 3 respectively.
Since 2 < 3, we conclude that 1/3 < 1/2. The fraction with the smaller result from cross-multiplication is the smaller fraction.
Further Exploration: Understanding Fraction Magnitude
Understanding the relationship between the numerator and denominator is key to grasping fraction magnitude. With a fixed numerator (like in our example where both fractions have a numerator of 1), the larger the denominator, the smaller the fraction. This is because the whole is divided into more parts, making each individual part smaller.
Addressing Common Misconceptions
- Larger Numerator = Larger Fraction: This is only true if the denominators are the same. If the denominators differ, comparing numerators alone is misleading.
- Ignoring Denominators: The denominator is just as important as the numerator in determining the value of a fraction. Ignoring it leads to incorrect comparisons.
- Intuitive Guessing: Relying on intuition without employing proper comparison methods can easily lead to incorrect conclusions. Always use a methodical approach.
Practical Applications: Real-World Examples
The ability to compare fractions is essential in many everyday situations:
- Baking: Following recipes accurately often requires comparing fractions (e.g., determining if 1/2 cup of sugar is more or less than 1/3 cup).
- Measurement: In construction or engineering, precise measurements necessitate comparing fractions of units (e.g., inches, meters).
- Finance: Calculating portions of budgets, shares, or investments frequently involves fraction comparisons.
- Data Analysis: Understanding proportions and percentages often involves converting fractions for comparison.
Frequently Asked Questions (FAQ)
-
Q: Can I always use the common denominator method? A: Yes, the common denominator method works for comparing any two or more fractions. It’s a reliable and universally applicable technique.
-
Q: Is cross-multiplication always accurate? A: Yes, cross-multiplication provides a quick and accurate way to compare two fractions. However, it's less intuitive for comparing more than two fractions.
-
Q: What if the fractions have different numerators and denominators? A: You can use any of the methods described above – common denominator, decimal conversion, or cross-multiplication – to compare fractions with different numerators and denominators.
-
Q: Are there other ways to compare fractions besides these three? A: While these three methods are the most common and widely used, you could also use visual aids such as number lines or area models to compare fractions.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics with broad applications in daily life. This article has demonstrated definitively that 1/3 is not greater than 1/2; in fact, 1/2 is greater than 1/3. We've explored various methods for comparing fractions, highlighting the importance of understanding the relationship between numerators and denominators. By mastering these techniques, you'll develop a stronger grasp of fractions and improve your ability to solve various mathematical problems and real-world challenges involving fractions. Remember to choose the method most comfortable and efficient for you, and always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
Convert Excel Time To Minutes
Sep 14, 2025
-
Fish Tank Water Volume Calculator
Sep 14, 2025
-
Can 5 15 Be Simplified
Sep 14, 2025
-
8 10 In Simplest Form
Sep 14, 2025
-
What Percentage Is 3 15
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1/3 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.