Is 1/8 Smaller Than 1/4
saludintensiva
Sep 23, 2025 · 5 min read
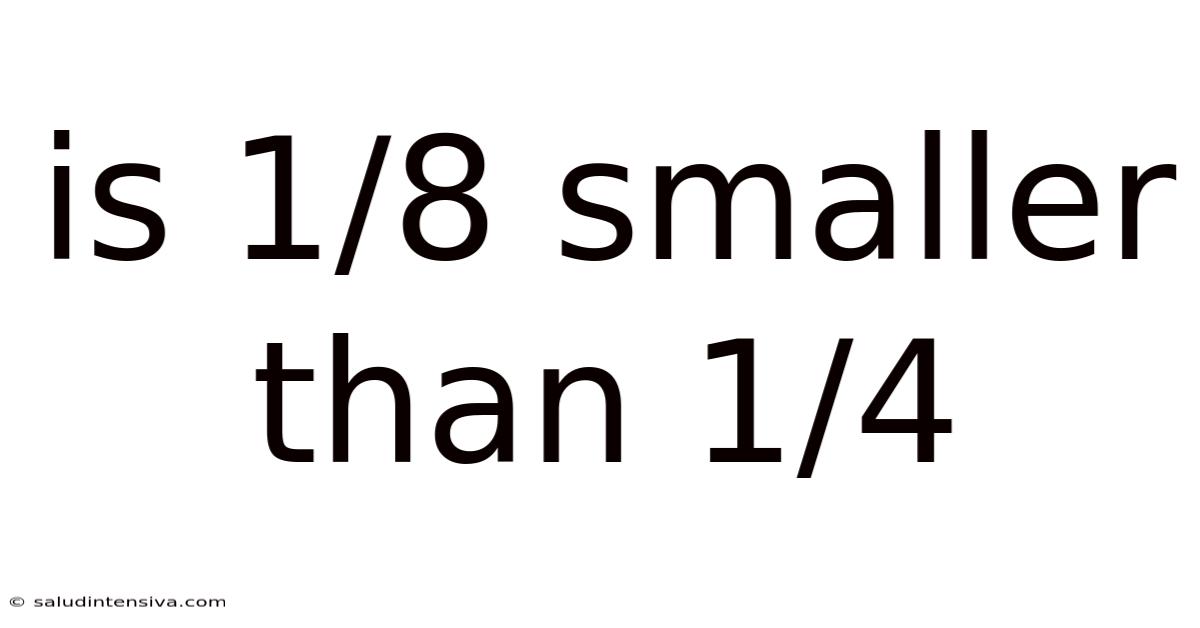
Table of Contents
Is 1/8 Smaller Than 1/4? A Deep Dive into Fractions
Understanding fractions is a fundamental skill in mathematics, essential for everyday life and further academic pursuits. This article will comprehensively address the question, "Is 1/8 smaller than 1/4?", exploring the concept of fractions, comparing different fractions, and providing practical examples to solidify your understanding. We'll delve into various methods of comparing fractions, including visual representations, decimal conversions, and finding common denominators. By the end, you'll not only know the answer to the initial question but also possess a robust understanding of fraction comparison.
Understanding Fractions: The Building Blocks
Before jumping into the comparison, let's establish a firm understanding of what fractions represent. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/4 (one-fourth), the numerator (1) signifies that we have one part, and the denominator (4) indicates that the whole has been divided into four equal parts. Similarly, 1/8 (one-eighth) represents one part out of eight equal parts.
Visualizing Fractions: A Picture is Worth a Thousand Words
A powerful way to grasp the concept of fractions is through visual representation. Imagine a pizza cut into four equal slices. Each slice represents 1/4 of the pizza. Now, imagine the same pizza cut into eight equal slices. Each slice now represents 1/8 of the pizza.
By visualizing these scenarios, it becomes immediately apparent that a single slice from a pizza cut into four pieces (1/4) is larger than a single slice from a pizza cut into eight pieces (1/8). This simple visual analogy provides a concrete understanding of the relative sizes of 1/4 and 1/8.
Comparing Fractions: Different Methods
There are several methods to compare fractions, each with its advantages:
1. Visual Comparison:
As we demonstrated with the pizza example, visualizing fractions can be intuitive and helpful, especially for smaller fractions. However, this method becomes less practical when dealing with larger or more complex fractions.
2. Decimal Conversion:
Converting fractions to decimals provides a straightforward comparison method. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 1/4 = 1 ÷ 4 = 0.25
- 1/8 = 1 ÷ 8 = 0.125
Comparing the decimal values, 0.25 is clearly larger than 0.125. Therefore, 1/4 is larger than 1/8.
3. Finding a Common Denominator:
This method is particularly useful when comparing fractions with different denominators. The goal is to rewrite both fractions with the same denominator, making direct comparison possible.
To find a common denominator for 1/4 and 1/8, we look for the least common multiple (LCM) of 4 and 8. The LCM of 4 and 8 is 8.
- We can rewrite 1/4 as an equivalent fraction with a denominator of 8 by multiplying both the numerator and denominator by 2: (1 x 2) / (4 x 2) = 2/8
Now we can compare 2/8 and 1/8 directly. Since 2/8 > 1/8, we confirm that 1/4 > 1/8.
The Answer: Yes, 1/8 is Smaller Than 1/4
Using any of the methods described above – visual representation, decimal conversion, or finding a common denominator – we definitively conclude that yes, 1/8 is smaller than 1/4.
Expanding Our Understanding: Working with More Complex Fractions
The principles discussed above apply to comparing any two fractions. Let's consider a few more examples to solidify our understanding:
-
Comparing 3/5 and 2/3: Finding a common denominator (15), we get 9/15 and 10/15. Therefore, 2/3 > 3/5.
-
Comparing 7/12 and 5/8: The common denominator is 24. We get 14/24 and 15/24. Therefore, 5/8 > 7/12.
-
Comparing 1/3 and 1/6: Visually, we can imagine a cake cut into 3 slices vs. 6 slices. A third of the cake is larger than a sixth. Alternatively, using a common denominator (6), we have 2/6 and 1/6, confirming 1/3 > 1/6.
Practical Applications: Real-World Examples of Fraction Comparison
Understanding fraction comparison is crucial in various real-world scenarios:
-
Cooking and Baking: Following recipes often requires understanding and comparing fractions of ingredients.
-
Measurement: Many projects, from carpentry to sewing, involve measuring and comparing fractional units (e.g., inches, centimeters).
-
Finance: Calculating percentages, interest rates, and discounts often involves working with fractions.
-
Data Analysis: Understanding proportions and ratios in data requires a solid grasp of fractions.
Frequently Asked Questions (FAQ)
Q: Why is the denominator important in comparing fractions?
A: The denominator indicates the size of the parts the whole is divided into. A smaller denominator signifies larger parts, while a larger denominator signifies smaller parts.
Q: What if the numerators are different, and the denominators are the same?
A: If the denominators are the same, the fraction with the larger numerator is the larger fraction. For example, 3/8 > 2/8.
Q: Is there a shortcut for comparing fractions?
A: For some simple fractions, visual comparison or a quick decimal conversion might suffice. However, finding a common denominator remains a reliable and generally applicable method.
Q: How can I improve my skills in working with fractions?
A: Practice is key! Work through numerous examples, utilize visual aids, and seek out online resources or tutoring if needed.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is a cornerstone of mathematical literacy. This article aimed to provide a comprehensive explanation of comparing fractions, particularly addressing the question of whether 1/8 is smaller than 1/4. We explored different methods for comparing fractions, highlighting their strengths and weaknesses. By mastering these concepts, you’ll not only answer simple fraction comparisons but also gain the foundational knowledge necessary to tackle more complex mathematical problems in various fields. Remember, the more you practice, the more confident and proficient you'll become in working with fractions.
Latest Posts
Latest Posts
-
6700 Sq Ft To Acres
Sep 23, 2025
-
X 2 8x 16 Factored
Sep 23, 2025
-
55 Acres To Sq Ft
Sep 23, 2025
-
How Long Is 25 Feet
Sep 23, 2025
-
Cubic Foot Of Concrete Weight
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Is 1/8 Smaller Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.