X 2 8x 16 Factored
saludintensiva
Sep 23, 2025 · 6 min read
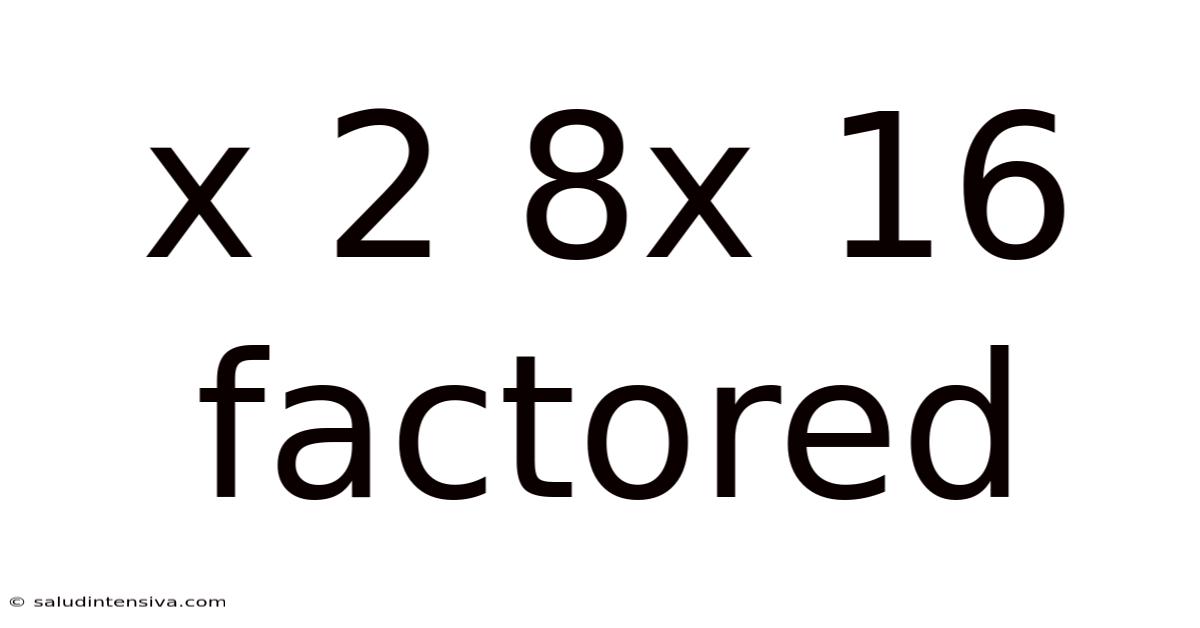
Table of Contents
Factoring Expressions: A Deep Dive into x² + 8x + 16
Understanding how to factor algebraic expressions is a fundamental skill in algebra. This article will provide a comprehensive guide to factoring the expression x² + 8x + 16, exploring various methods, explaining the underlying principles, and extending the concept to similar problems. We'll move beyond simply finding the answer to develop a deep understanding of the process and its applications.
Introduction: What is Factoring?
Factoring, in the context of algebra, is the process of breaking down a polynomial expression into simpler expressions that, when multiplied together, give the original polynomial. Think of it like reverse multiplication. Instead of multiplying factors together to get a product, we're starting with the product and finding the factors. This skill is crucial for simplifying expressions, solving equations, and tackling more advanced algebraic concepts. Our focus will be on factoring quadratic trinomials, which are expressions of the form ax² + bx + c, where a, b, and c are constants. The expression x² + 8x + 16 is a prime example of such a trinomial.
Method 1: The Factoring by Inspection Method
This method relies on observation and understanding the relationship between the coefficients and the factors. We're looking for two numbers that add up to the coefficient of the x term (8 in this case) and multiply to the constant term (16).
Let's break it down:
- Find the factors of 16: The pairs of factors of 16 are (1, 16), (2, 8), and (4, 4).
- Identify the pair that adds up to 8: The pair (4, 4) adds up to 8.
Therefore, we can write the factored form as (x + 4)(x + 4), or more concisely as (x + 4)². This is a perfect square trinomial.
Method 2: The FOIL Method in Reverse
The FOIL method (First, Outer, Inner, Last) is typically used for expanding factored expressions. We can reverse this process to factor. Remember that (a + b)(c + d) = ac + ad + bc + bd.
Let's apply this to our expression:
We're looking for two binomials (x + a)(x + b) that when multiplied using the FOIL method yield x² + 8x + 16.
- First: x * x = x² (This matches our expression)
- Outer: x * b = bx
- Inner: a * x = ax
- Last: a * b = 16
Combining the outer and inner terms, we have (a + b)x. We need this to equal 8x, so a + b = 8. Since a * b = 16, and we know the pair (4, 4) satisfies both conditions, our factors are (x + 4) and (x + 4).
Therefore, the factored form is again (x + 4)².
Method 3: Completing the Square
Completing the square is a more general method that can be used to factor any quadratic expression, even those that don't factor easily by inspection.
- Identify the coefficient of x: The coefficient of x is 8.
- Take half of the coefficient and square it: (8/2)² = 16. Note that this is our constant term.
- Rewrite the expression: x² + 8x + 16 can be rewritten as (x² + 8x + 16). This is a perfect square trinomial.
- Factor the perfect square trinomial: This factors as (x + 4)².
This method highlights the special structure of a perfect square trinomial, demonstrating that x² + 8x + 16 is indeed a perfect square.
Explanation: Perfect Square Trinomials
The expression x² + 8x + 16 is a perfect square trinomial because it can be factored into the square of a binomial. The general form of a perfect square trinomial is a² + 2ab + b² = (a + b)². In our case, a = x and b = 4, so we have x² + 2(x)(4) + 4² = (x + 4)². Recognizing this pattern can significantly speed up the factoring process.
Applications of Factoring
Factoring isn't just an abstract algebraic exercise; it has numerous applications:
- Solving Quadratic Equations: Factoring is a key technique for solving quadratic equations of the form ax² + bx + c = 0. Once factored, the equation can be easily solved by setting each factor equal to zero. For example, (x + 4)² = 0 implies x + 4 = 0, so x = -4.
- Simplifying Expressions: Factoring simplifies complex algebraic expressions, making them easier to manipulate and understand.
- Calculus: Factoring is fundamental in calculus, particularly in finding derivatives and integrals.
- Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts of its corresponding parabola, making it easier to graph the function.
Extending the Concept: Similar Factoring Problems
Let's explore some variations to solidify your understanding:
- x² + 10x + 25: This is another perfect square trinomial, which factors to (x + 5)². Can you find the factors using the methods described above?
- x² - 6x + 9: This is also a perfect square trinomial, but note the negative sign in the middle term. This will result in (x - 3)². The process remains the same; just be mindful of signs.
- x² + 7x + 12: This trinomial is not a perfect square but can still be factored using the methods we've discussed. Think about the pairs of factors of 12 that add up to 7. This factors into (x + 3)(x + 4).
- x² - 5x + 6: Again, be mindful of the negative signs. This factors into (x - 2)(x - 3).
Frequently Asked Questions (FAQ)
- What if the expression can't be factored? Not all quadratic expressions can be factored using integer coefficients. In these cases, you might need to use the quadratic formula to find the roots.
- Why is factoring important? Factoring is a fundamental algebraic skill that simplifies expressions, allows you to solve equations, and is crucial for more advanced mathematical concepts.
- What are some common mistakes to avoid when factoring? Common mistakes include incorrect signs, overlooking factors, and not checking your work by expanding the factored form to verify that it matches the original expression.
Conclusion: Mastering Factoring
Mastering factoring is a crucial step in your algebraic journey. By understanding the different methods – inspection, the FOIL method in reverse, and completing the square – and by practicing with various examples, you'll develop a strong foundation for more advanced mathematical concepts. Remember to always check your work by expanding the factored form to ensure it matches the original expression. Through consistent practice and a deep understanding of the underlying principles, you can confidently tackle any factoring problem that comes your way. The journey might seem challenging at first, but with perseverance, factoring will become second nature. Remember to break down complex problems into smaller, manageable steps, and don't hesitate to review the different methods to find the approach that suits you best. This comprehensive understanding will not only help you solve immediate problems but also equip you with a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
Cost Of Formula Per Month
Sep 23, 2025
-
Air Tank Fill Near Me
Sep 23, 2025
-
45 Days From 12 31
Sep 23, 2025
-
Adding Same Base Different Exponents
Sep 23, 2025
-
15 3 4 Divided By 2
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 8x 16 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.