Is 2/3 Equal To 6/9
saludintensiva
Sep 15, 2025 · 5 min read
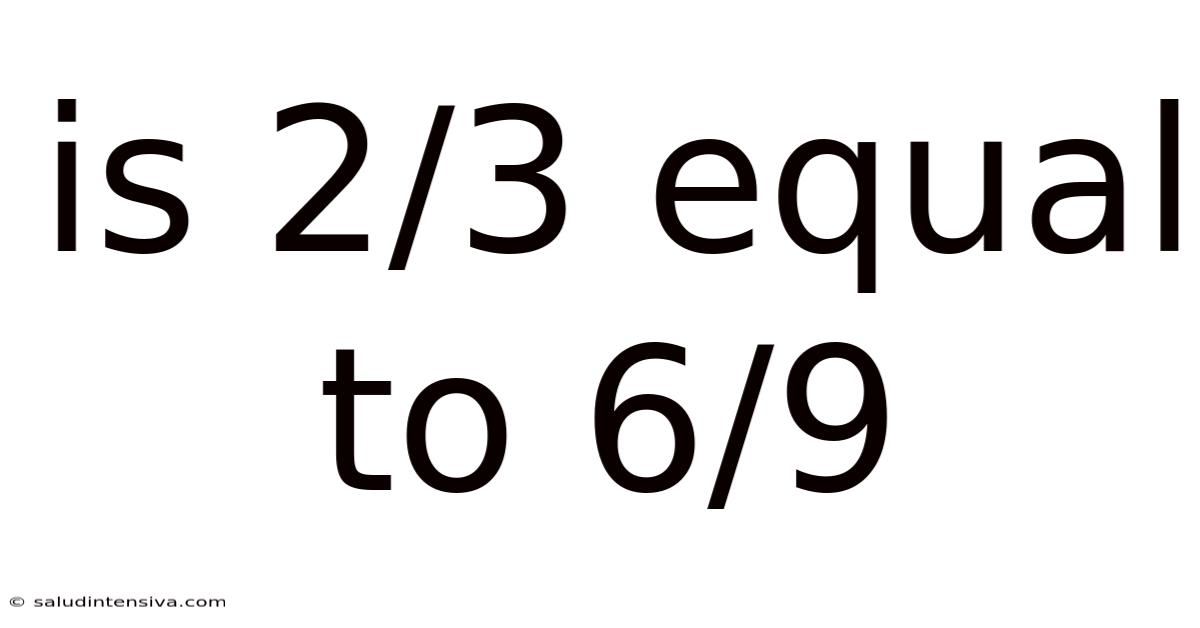
Table of Contents
Is 2/3 Equal to 6/9? A Deep Dive into Fractions and Equivalence
Are you puzzled by fractions? Do you wonder if seemingly different fractions, like 2/3 and 6/9, actually represent the same amount? This article will explore the concept of equivalent fractions, demonstrating why 2/3 and 6/9 are indeed equal and providing you with the tools to confidently tackle similar comparisons. We’ll move beyond a simple “yes” or “no” to give you a thorough understanding of the underlying mathematical principles.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering. For instance, in the fraction 2/3, the whole is divided into 3 equal parts, and we're looking at 2 of those parts.
Visualizing Equivalence: The Pizza Analogy
Let's use a pizza to illustrate the equivalence of 2/3 and 6/9. Imagine a large pizza cut into 9 equal slices. If you eat 6 of those slices, you've eaten 6/9 of the pizza. Now, imagine a smaller pizza cut into 3 equal slices. If you eat 2 slices of this pizza, you've eaten 2/3 of it.
Although the pizzas are different sizes and the number of slices varies, notice that the portion consumed is the same in both scenarios. This visual representation helps to grasp the concept of equivalent fractions—fractions that represent the same proportion or value, even though they look different.
Mathematical Proof: Simplifying and Expanding Fractions
The most straightforward way to prove that 2/3 and 6/9 are equal is through the principles of simplifying and expanding fractions.
-
Simplifying Fractions: Simplifying a fraction means reducing it to its lowest terms. We do this by finding the greatest common divisor (GCD) of the numerator and the denominator, and then dividing both by the GCD. The GCD of 6 and 9 is 3.
6 ÷ 3 = 2 9 ÷ 3 = 3
Therefore, 6/9 simplifies to 2/3.
-
Expanding Fractions: Expanding a fraction involves multiplying both the numerator and the denominator by the same number. This doesn't change the value of the fraction, only its representation. Let's expand 2/3:
If we multiply both the numerator and the denominator by 3:
2 × 3 = 6 3 × 3 = 9
This gives us 6/9.
Since we can simplify 6/9 to 2/3 and expand 2/3 to 6/9, it definitively proves that 2/3 = 6/9.
Understanding the Concept of Proportionality
The equivalence of fractions hinges on the concept of proportionality. Two fractions are equivalent if the ratio between their numerators and denominators is the same. We can express this as a proportion:
2/3 = 6/9
To check if this proportion is true, we can cross-multiply:
2 × 9 = 18 3 × 6 = 18
Since the cross-products are equal, the proportion is true, confirming that 2/3 and 6/9 are equivalent.
Applications of Equivalent Fractions in Real-Life Scenarios
Understanding equivalent fractions is crucial in various real-world applications:
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. Knowing how to find equivalent fractions allows you to scale recipes up or down accurately. For example, if a recipe calls for 1/2 cup of sugar and you want to double the recipe, you'll need 1/2 + 1/2 = 2/2 = 1 cup, or any equivalent fraction such as 2/2, 4/4, etc.
-
Measurement and Units: Converting between different units of measurement frequently involves equivalent fractions. For instance, converting inches to feet or centimeters to meters necessitates understanding how to represent the same quantity using different units.
-
Finance and Budgeting: Equivalent fractions are useful when dealing with percentages, ratios, and proportions in financial calculations. Understanding how to simplify and manipulate fractions can improve accuracy in budgeting and financial planning.
-
Geometry and Spatial Reasoning: Equivalent fractions are essential in geometric calculations, especially when dealing with areas, volumes, and similar figures.
Beyond 2/3 and 6/9: Identifying Equivalent Fractions
The techniques demonstrated with 2/3 and 6/9 can be applied to any pair of fractions. To determine if two fractions are equivalent, you can:
-
Simplify both fractions to their lowest terms: If they simplify to the same fraction, they are equivalent.
-
Cross-multiply: If the cross-products are equal, the fractions are equivalent.
-
Find a common denominator: Convert both fractions to have the same denominator. If the numerators are then equal, the fractions are equivalent.
Frequently Asked Questions (FAQ)
Q1: Are there infinitely many equivalent fractions for any given fraction?
A1: Yes, absolutely. You can expand any fraction by multiplying its numerator and denominator by any non-zero integer. This generates an infinite number of equivalent fractions.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand and work with. It provides the most concise and efficient representation of the fraction's value. It also makes calculations simpler and less prone to errors.
Q3: Can I use a calculator to check if two fractions are equivalent?
A3: While a calculator can help compute decimal equivalents, it doesn't directly show the equivalence using the principles of fractions. It's best to understand the underlying mathematical concepts for a complete understanding. However, comparing the decimal equivalents can provide a quick check.
Q4: What if the fractions have different signs (positive and negative)?
A4: The principles remain the same, but you need to consider the signs. If one fraction is positive and the other negative, they are not equivalent. If both are negative, treat them as positive, simplify or compare, and if they are equivalent, then the original negative fractions are also equivalent.
Conclusion: Mastering the Fundamentals of Fractions
The seemingly simple question, "Is 2/3 equal to 6/9?" opens a door to a broader understanding of fractions and their equivalence. By mastering the principles of simplifying, expanding, and using proportionality, you gain a powerful toolset for tackling various mathematical challenges and real-world problems that involve fractions. Remember, the ability to confidently manipulate and compare fractions is a fundamental skill with far-reaching applications across diverse fields. So, next time you encounter a fraction, remember the pizza analogy and the steps outlined here – you’ll be well-equipped to conquer any fractional challenge that comes your way!
Latest Posts
Latest Posts
-
1 19 As A Decimal
Sep 15, 2025
-
How Much Is 90 Days
Sep 15, 2025
-
1 4 In A Percentage
Sep 15, 2025
-
What Is 1 3 Times 2 3
Sep 15, 2025
-
18 20 As A Decimal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Equal To 6/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.