Is 2/3 Greater Than 1/3
saludintensiva
Sep 14, 2025 · 6 min read
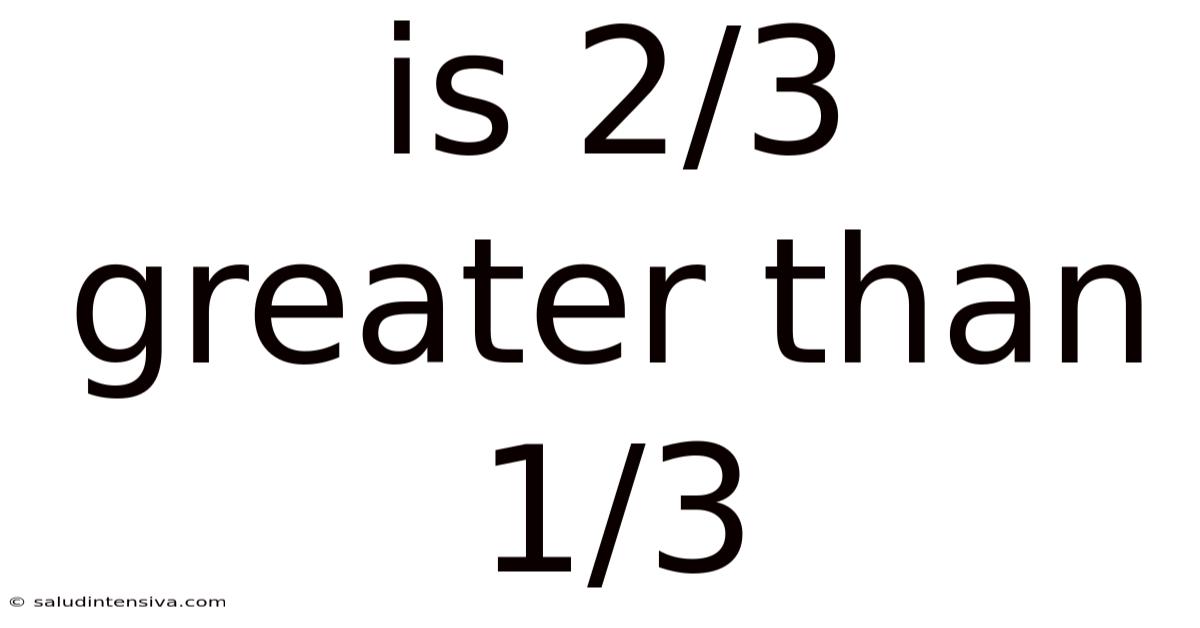
Table of Contents
Is 2/3 Greater Than 1/3? A Deep Dive into Fractions
This article explores the seemingly simple question: is 2/3 greater than 1/3? While the answer might seem obvious to many, a deeper understanding of fractions provides valuable insights into mathematical concepts applicable far beyond this basic comparison. We'll delve into the fundamentals of fractions, explore various methods for comparing them, and address common misconceptions. This comprehensive guide will equip you with the tools to confidently tackle more complex fractional comparisons in the future.
Understanding Fractions: Building Blocks of Mathematics
Before diving into the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator shows how many of those parts are being considered.
For example, in the fraction 1/3, the denominator (3) means the whole is divided into three equal parts. The numerator (1) indicates that we're considering one of those three parts. Similarly, 2/3 represents two out of three equal parts of the whole.
Visualizing the Comparison: The Power of Representation
One of the most effective ways to understand the comparison between 2/3 and 1/3 is through visualization. Imagine a pizza cut into three equal slices.
- 1/3: Represents one slice of the pizza.
- 2/3: Represents two slices of the pizza.
Clearly, two slices are more than one slice. Therefore, 2/3 is greater than 1/3. This visual representation provides an intuitive grasp of the concept, making it easier to internalize. This simple analogy can be extended to various real-world scenarios involving sharing, measuring, or proportions.
Comparing Fractions: Different Approaches
While visualization is helpful for basic comparisons, more rigorous methods are needed for more complex fractions. Here are several approaches:
1. Common Denominator Method: This is a fundamental method for comparing fractions. If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction. In our case, both 2/3 and 1/3 already have the same denominator (3). Since 2 > 1, 2/3 > 1/3.
2. Decimal Conversion Method: Converting fractions to decimals allows for easy comparison. To convert a fraction to a decimal, divide the numerator by the denominator.
- 1/3 = 0.333... (a repeating decimal)
- 2/3 = 0.666... (a repeating decimal)
Since 0.666... > 0.333..., we confirm that 2/3 > 1/3.
3. Cross-Multiplication Method: This method is particularly useful when comparing fractions with different denominators. To compare fractions a/b and c/d, cross-multiply: ad and bc. The larger product corresponds to the larger fraction. While not strictly necessary in this instance (as both fractions share a denominator), it's a valuable technique for broader fractional comparison.
Addressing Common Misconceptions
Despite the simplicity of this comparison, some common misconceptions can arise:
-
Ignoring the denominator: Some might mistakenly focus solely on the numerators, concluding that 1 is smaller than 2, therefore 1/3 is smaller than 2/3. This is incorrect because the denominator defines the size of each part.
-
Confusing numerators and denominators: A misunderstanding of the roles of the numerator and denominator can lead to incorrect comparisons. Remembering that the denominator represents the size of the parts is crucial.
Extending the Concept: Proportion and Ratio
Understanding the relationship between 2/3 and 1/3 lays the groundwork for understanding more complex concepts like proportions and ratios. A ratio is a comparison of two or more quantities. In this case, the ratio of 2/3 to 1/3 is 2:1, meaning there are twice as many parts in 2/3 as in 1/3. This concept is fundamental in various fields, including cooking, engineering, and finance.
Real-World Applications: From Pizza to Percentages
The comparison of 2/3 and 1/3 isn't just an abstract mathematical exercise; it has numerous real-world applications. Consider these examples:
-
Sharing resources: If you have three cookies and need to share them equally among three friends, each friend receives 1/3 of the cookies. If you have six cookies and share them among three friends, each receives 2/3.
-
Calculating percentages: Understanding fractions helps in calculating percentages. 2/3 is equivalent to approximately 66.67%, while 1/3 is approximately 33.33%. These percentages are frequently used in sales, discounts, and statistics.
-
Measurement and scaling: Fractions are essential in various fields that involve precise measurements, such as construction, engineering, and carpentry. Understanding the relationship between 2/3 and 1/3 is critical for scaling projects and ensuring accuracy.
Beyond the Basics: Working with More Complex Fractions
The principles applied to comparing 2/3 and 1/3 can be extended to more complex fraction comparisons. For instance, comparing 5/8 and 3/4 would involve finding a common denominator (in this case, 8) and then comparing the numerators (5 and 6). The same principles of visualization, decimal conversion, and cross-multiplication remain applicable.
Frequently Asked Questions (FAQ)
Q1: Is there a quick way to tell if one fraction is larger than another without performing calculations?
A1: If the fractions have the same denominator, the fraction with the larger numerator is greater. If they have the same numerator, the fraction with the smaller denominator is greater. However, for fractions with different numerators and denominators, it's generally best to use a method like finding a common denominator or cross-multiplication.
Q2: What if the fractions are negative? How does that affect the comparison?
A2: With negative fractions, the rules are reversed. The fraction with the larger absolute value (ignoring the negative sign) is smaller. For instance, -1/3 > -2/3 because -1/3 is closer to zero on the number line.
Q3: How can I improve my understanding of fractions?
A3: Practice is key. Solve various fraction problems, use visual aids like diagrams and manipulatives, and try real-world applications to solidify your understanding.
Conclusion: Mastering the Fundamentals
The comparison of 2/3 and 1/3, while seemingly simple, serves as a foundational building block for understanding more complex mathematical concepts. By grasping the principles of fractions, visualization techniques, and different comparison methods, you gain a valuable skill set applicable across numerous fields. Remember to practice regularly and apply your knowledge to real-world scenarios to reinforce your understanding and build confidence in tackling more challenging fractional problems. The ability to confidently compare and manipulate fractions is essential for success in mathematics and various other areas. So keep practicing, keep exploring, and enjoy the power of fractions!
Latest Posts
Latest Posts
-
The Amount Of Each Payment
Sep 14, 2025
-
60 Minutes In 1 Hour
Sep 14, 2025
-
1 2 3 Or 4
Sep 14, 2025
-
How Many Inches Is 18cm
Sep 14, 2025
-
Is 2 3 Larger Than 3 4
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Greater Than 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.